圆锥曲线的两个共同性质

江苏省东海高级中学 (222300) 孙通喜

结论一已知曲线C：mx2+ny2=1以及一点P(x0,y0)(P点不在曲线C上)，过P点作两条斜率互为相反数的直线l1，l2，分别交曲线C与A、B、C、D，则有PA·PB=PC·PD.

结论二已知抛物线C：y2=2px(p>0)及点P(x0,y0)(P点不在曲线C上)，过P点作两条斜率互为相反数的直线l1，l2，分别交C与A，B，C，D，则PA·PB=PC·PD.

综上，我们有:

定理一过平面内一点P作两条斜率互为相反数的直线l1，l2，分别与圆锥曲线交于不同的两点A,B,C,D，则有PA·PB=PC·PD.

图1

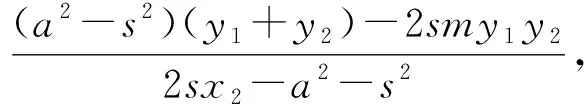
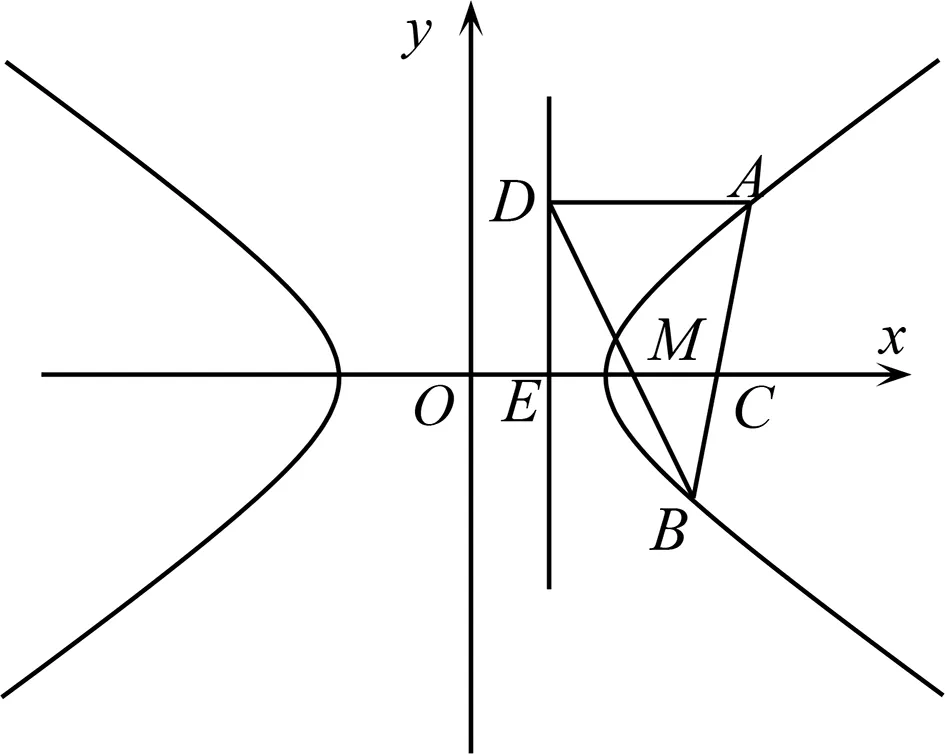
图2

证明同结论三，读者可以自行证明.

综上，我们有：

上述结论对于抛物线也有相同的结论，读者不妨自己试试.