一道变系数胡不归问题详探

厦门大学附属实验中学 (363123) 杨 坤 林运来

1 试题呈现

在如图1所示的Rt△ABC中,∠C=90°，∠A=30°，BC=5，P为AC上一动点,则2BP+AP的最小值为.

图1

本题是典型的胡不归问题,题虽小,意且长. 出自先秦佚名的《国风·邶风·式微》的胡不归问题,由于其较强的文学性和源远流长的数学文化日益成为中学数学考试中的热点难点问题.笔者查阅资料发现,长久以来关于胡不归问题的解法相对单一(解法1),且仅仅局限于几何构造,较少代数解法.随着学生数学学习的不断深入,解法应该逐步多样.基于维果斯基的最近发展区理论,解题教学也要基于学生的现有发展水平,为此根据学生的不同学习阶段,笔者依次提供以下解法:

2 解法探究

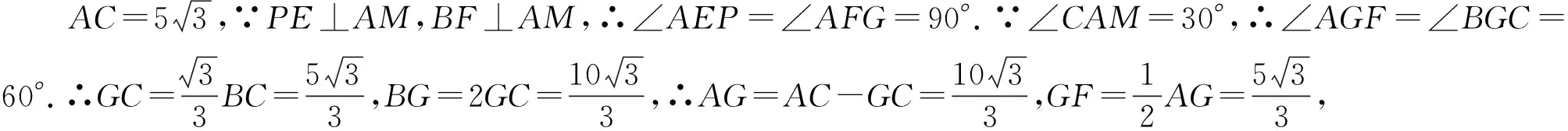
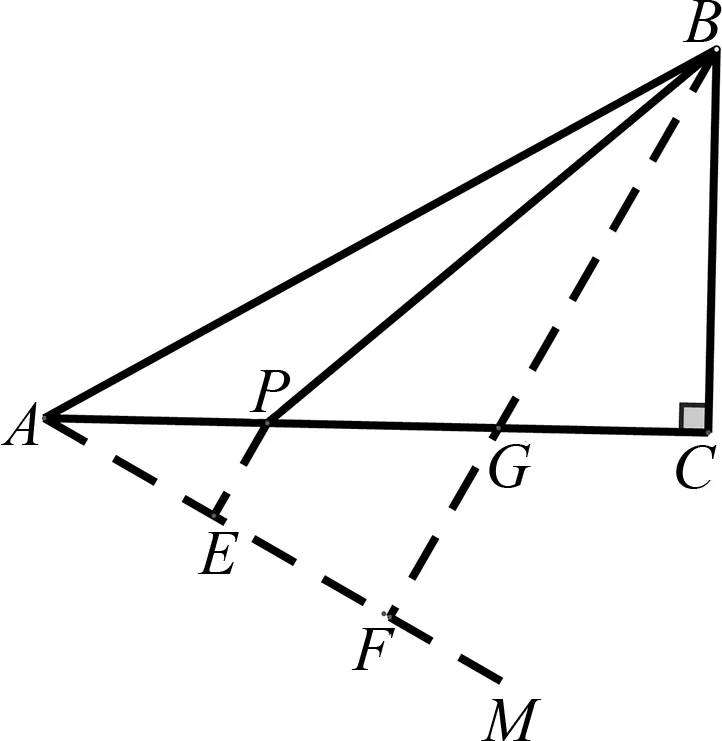
图2

评注：解法1是胡不归类型的典型解法,在初中学完直角三角形即可应用.但学生初次接触时极难想到提系数,只有经过启发练习后才能初步掌握.

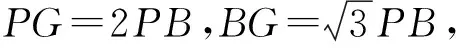
图3

评注：解法2学完相似三角形即可应用,但此法是非典型的线段构造,强调的是动点的轨迹(轨迹方程).

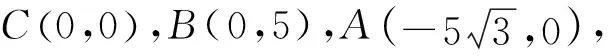
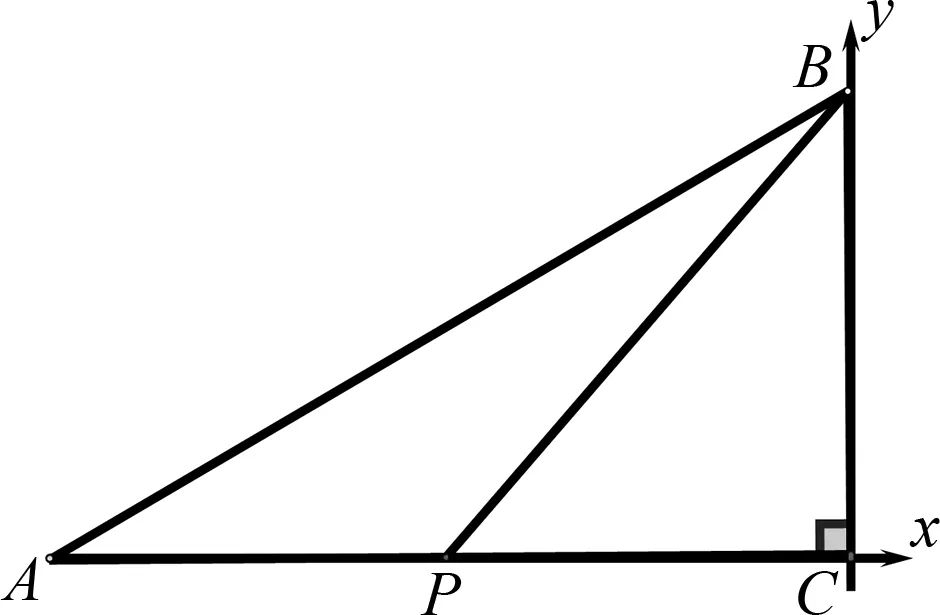
图4

评注：解法3在学完一元二次方程即可应用,但是要求较高的数学抽象能力和极好的数学运算能力.

评注：解法4在学习完三角函数即可应用,但由于对此种问题的三角换元望而却步,实际教学效果一般.

评注：解法5在学习完导数后即可应用,但高中生虽然会导数求最值,却对根式求导不敢轻易尝试.

3 解后反思

根据维果斯基最近发展区理论,解题教学一定要掌握学生目前的发展水平,进而设置与之相当的题目,激发其兴趣,利用其潜能,从而超越其最近发展区而达到下一阶段的发展水平，然后在此基础上进行下一个发展区的发展.为完成此目标,示范、引导和激励学生掌握多种不同阶段和层次的解法,以及各种解法之间的对比也是尤为必要的.当然,本文中的几种解法并未穷尽所有解法思路.但是,这些不同的解法涉及到许多的解题思路,运用了不少知识点,解题教学中多进行此种小题的解题思维训练,能有助于进一步减轻学生的学习负担,提高学生的逻辑思维水平,从而达到提升学生的创新精神和探索能力.