挖掘不等关系 妙求椭圆离心率的范围
江苏省苏州市田家炳实验高级中学 (215000) 何小寅
离心率的范围问题是高考的热点题目之一,各种题型均有涉及,因涉及的知识点较多,且处理问题的思路和方法比较灵活,而此类问题解题关键是如何确定不等关系式,也就是得到一个关于离心率的不等式,再通过解不等式求得离心率范围.本文通过题例分析,介绍挖掘不等关系求椭圆离心率范围六种思路,供读者朋友参考.
一、抓住几何图形中的不等关系
根据平面图形的关系,如三角形两边之和大于第三边、折线段大于或等于直线段、对称的性质中的最值等得到不等关系,然后将这些量结合曲线的几何性质用a,b,c进行表示,进而得到不等式,从而确定离心率的范围.
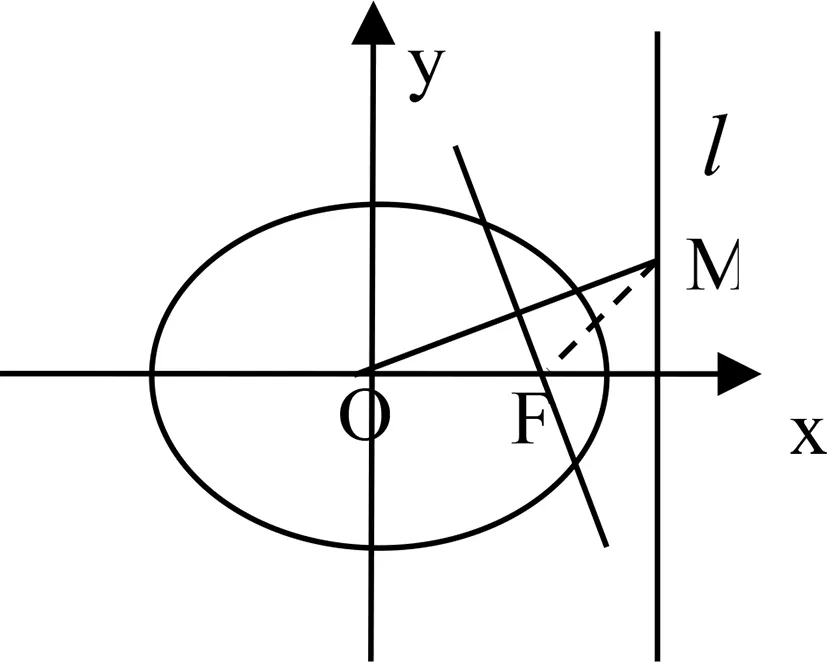
图1
例1 已知椭圆的中心在O,右焦点为F,右准线为l,若在l上存在点M,使线段OM的垂直平分线经过点F,求此椭圆的离心率的取值范围.
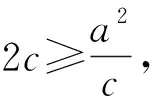
点评:离心率的范围实质为一个不等式关系,如何构建这种不等关系?可以利用方程和垂直平分线性质构建.利用题设和平面几何知识的最值构建不等式往往使问题简单化.
二、抓住题目中给出的不等信息
根据题目本身给出的不等条件,如已知某些量的范围,存在点或直线使方程成立,Δ的范围等,进一步得到离心率的不等关系式,从而求解.

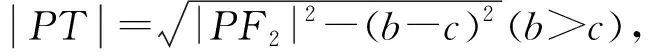
点评:本题主要考查了椭圆标准方程中相关元素的关系,抓住已知的不等式求范围是成功解题的一个重要环节.特别须注意对隐含条件挖掘,如本题中的b>c.
三、利用三角函数确定不等关系
在一些题目中会采用角度表示相关几何图形的变化,我们如果能够用三角函数表示有关的线段长建立相关的等式或不等式,最后就可运用三角函数值的范围解决问题.


图2
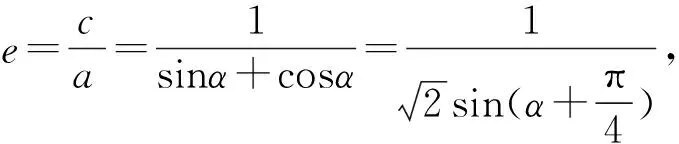

四、利用代数式的变形得到不等关系
利用曲线的定义、等量关系等条件建立离心率和其他一个变量的函数关系式,通过代数式的运算确定表达式的变化范围,达到求解离心率的范围的目的.

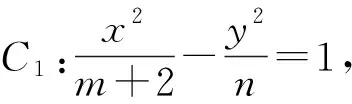
五、利用动点在椭圆上用定义得到不等关系
椭圆的定义是所有椭圆问题的根本所在,若条件中含有一动点在相关曲线上,能想到运用此曲线的定义解题是非常好的思路之一.
例5 设椭圆的两个焦点为F1,F2,若椭圆上恒存在一点P,使∠F1PF2=120°,求椭圆离心率的范围.

点评:通过整体的把握题意,在余弦定理和基本不等式等知识的支持下,构造出关于a、c的不等式.
六、利用椭圆的性质得到不等关系



点评:注意到P为椭圆上的一点是本题的关键条件,根据圆锥曲线的共同特征把|PF1|·|PF2|=2c2转化成基本量a,c,e与x0的关系式,结合椭圆的范围,即可得到e的不等式,从而就顺利求出了离心率的范围.
以上典型例题的分析探究,介绍了灵活运用不等关系求椭圆离心率的范围问题,有一些可能是老生常谈,但作为系统方法的表述,这里不得不再一次强调.在具体解题中,根据问题特点可能会有许多其它特殊的方法,限于篇幅,这里只能无情割爱了.

