极坐标巧解涉及多点联动问题的最值

安徽省亳州市第十八中学 (236800) 郭中华 张官升 陈 思

近年来，各种联考中涉及求解三角形边长、面积的最值问题，一直以压轴小题形式出现，试题求解往往是利用正余弦定理来解决，但关系复杂、计算繁琐，特别是其中的联动点的轨迹问题更为繁琐.这类问题利用极坐标的思想方法来求解相对容易.本文从三个方面例析寻找隐圆方法求其最值.

1 涉及动点到定点的距离最值

例1 已知圆O：x2+y2=1，若A,B是圆O上两个不同的两点，以AB为边作等边△ABC，则线段OC的最大值是( ).

图1

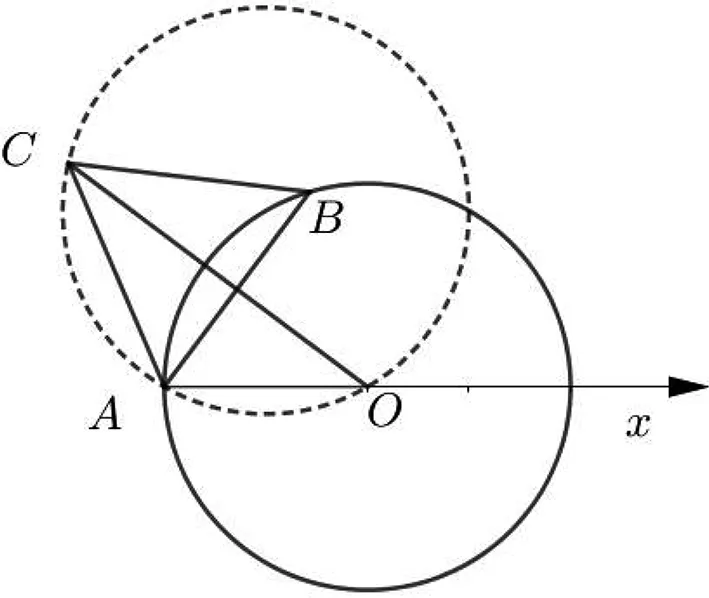
图2

评析：本题中A,B,C均为动点，已知点A,B在定圆上，点C随着A,B的运动而运动. 且动点C(x,y)坐标之间的关系不明确. 因为两个点都在运动，所以不容易判断，求解中通过先固定点A，再观察到点B在圆上的运动，那么联动点C的运动轨迹就很容易发现. 再利用GeoGebra画图软件的追踪工具，便可以发现点C的轨迹是一个圆. 由于点C、B为联动点，所以其轨迹形状相似. 通过建立极坐标系的方法，由B点的轨迹和固定角∠CAB=60°，求出C的轨迹.

2 求有固定夹角的两动点距离最值

图3

评析：本题是多点联动类问题，根据条件先固定D点，由动点A,B都在以D为圆心的圆上，再根据联动原理，易知动点C的轨迹也是一个圆. 再建系处理点B、C的轨迹. 进而求出圆的轨迹方程达到求出CD的最小值.

3 求三角形面积的最值

例3 如图4所示，在平面四边形ABCD中，已知AB=1,BC=2,△ACD为正三角形，求△BCD的面积的最大值.

图4

图5

评析：本题涉及到多点联动变化而引起的面积最值类问题.动点A在以点B为圆心的圆上，根据联动原理，可知动点D的轨迹也是一个圆. 通过求出圆的极坐标方程就可以解决三角形顶点D到底边BC的最大值求解问题，由此求得△BCD面积最大值.