巧用同构方法构造函数解决复杂问题
江苏省溧阳中学 (213300) 徐 兰
江苏省连云港市锦屏高级中学 (222021) 车树勤
同构式是指变量不同,结构、形式都相同的数学表达式.同构的过程就是通过移项、拆分、配凑等手段将一个数学表达式恒等变形,使其左右两边呈现形式、结构完全一样的状态,然后构造辅助函数,通过辅助函数的性质来解决问题.下面我们来体验一下同构之路.
一、同构的初级阶段
例1 (2020年全国1卷12题)若2a+log2a=4b+2log4b,则( ).
A.a>2bB.a<2bC.a>b2D.a 解析:2a+log2a=4b+2log4b=22b+log2b=22b+log22b-1.设函数f(x)=2x+log2x,∴原不等式等价于f(a)=f(2b)-1 例2 (2020年八省联考)已知a<5且ae5=5ea,b<4且be4=4eb,c<3且ce3=3ec,则( ). A.c C.a A.(-∞,e] B.(-∞,e) 评注:本题中的两个变量x2、x1不关联,采用集中变量后出现了结构相同的式子,于是构造新的函数u(x)=xf(x), 利用函数的单调性来解决问题. 在以上的问题中构造出同构式的要求有所提高,但难度系数不大.这两个问题的解决中,都是对表达式进行集中变量的变形就能得到相同的结构,构造出新的函数,通过导数研究函数的单调性就可以解决问题. 第四步:把原不等式用复合函数的形式表达出来f(e-x)≥f(xa),并分析内函数的取值范围⟹原不等式等价于f(e-x)≥f(xa),∵x∈(1,+∞),e-x∈(0,1),又由选项可知只需研究a<0的情况,a<0时,xa∈(0,1); 第五步:根据函数f(x)在(0,1)上单调递减,把f(e-x)≥f(xa)转化为e-x与xa之间的关系⟹e-x≤xa; 评注:利用指数对数运算的之间的内部关系,我们可以构造相同的结构e-x-lne-x≥xa-lnxa,通过构造新的函数f(x)=x-lnx,原不等式就可以等价变形为f(e-x)≥f(xa),从而转化为基本函数中利用函数的单调性来解决的常见不等式问题.达到了化陌生为熟悉的效果. (1)函数f1(x)=x±lnx=elnx±lnx,与g1(x)=ex±x同构,或者变换g1(x)=ex±x=ex±lnex,与f1(x)=x±lnx同构; (3)函数f3(x)=xlnx=elnxlnx与g3(x)=xex同构;或者变换g3(x)=xex=exlnex与f3(x)=xlnx同构. 可以发现,指对同构的过程中的核心是lnex=x=elnx,也就是利用指幂运算来构造相同的结构,指对同构的主要方法是指对式分离,找出内层函数.同构的演变题型其实就是命题人把一个结构整齐的同构式重新打乱,重组,变有序为无序,而我们要做的是将这打乱的式子按照一定的目标进行整合变形,合理拆分,使其恢复原貌,化复杂为简单,利用同构构造出一个新的函数,把原式写成复合函数的形式,再利用外层函数的性质转变为内层函数之间的关系,达到化繁为简. 弄清楚这种解法的数学思维起点在哪里,解决问题的数学本质是什么. 例5 (2020年山东高考卷第21题)已知函数f(x)=aex-1-lnx+lna.(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积:(2)若f(x)≥1,求a的取值范围. 解析:(1)略.(2)中的这个不等式恒成立,既有指数式又有对数式,不妨用指对分离来试一试. 第一步:分离指对式,变换出lna⟹elnaex-1≥-lna+lnx+1; 第二步:变换为同构式,找到内函数lna+x-1⟹elna+x-1+lna+x-1≥lnx+x; 第三步:构造函数f(x)=ex+x,且在定义域(-∞,+∞)上为单调增函数; 第四步:原不等式等价于f(lna+x-1)≥f(lnx)恒成立; 第五步:根据函数f(x)的单调性,转化为lna+x-1≥lnx恒成立; 第六步:分离出lna,lna≥(lnx-x+1)max.令g(x)=lnx-x+1,求导求出最大值为0.∴lna≥0,解之a≥1. 通过以上分析,同构的演变题型都可以用这六步骤来解决问题,同构的外层函数总是由指数或对数函数与一次函数的组合而成,一旦式子两边构造出相同结构,就可以构造出新的函数,把一个很复杂的问题转化为一个常见函数的性质来解决,难点就是对结构的变形处理,灵活处理指幂运算来达到自己想要的效果.
二、同构的发展阶段

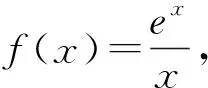



三、同构的演变阶段