立足培养数学核心素养的解题教学*
——以一道三角结构不良试题为例
福建省厦门第一中学 (361003) 王淼生
1 联考真题呈现
试题在①tanB=2tanC,②3b2-a2=12,③bcosC=2ccosB三个条件中任选一个,补充在下面问题中的横线上,并解决该问题.
问题:已知△ABC的内角A,B,C及其对边a,b,c,若c=2,且满足,求△ABC的面积的最大值.(注:如果选择多个条件分别解答,按第一个解答计分.)(2021年名校联盟优质校高三大联考第18题)
2 结构不良试题
Reitman(1965)首次从认知心理学层面提出结构良好问题与结构不良问题的理论.将这一理论迁移到数学问题,形成结构良好试题与结构不良试题.长期以来,高考数学试题中主要考查结构良好试题.随着高考命题理念从最早的“知识立意”到后来的“能力立意”再到如今的“价值引领、素养导向、能力为重、知识为基”转变,旨在优化学生思维,发展学生智力,提升学生素养,落实立德树人的根本任务.自从2016年教育部考试中心提出构建高考评价体系以来,近年逐步出现结构不良试题,并越来越受到关注.尽管目前对结构不良数学试题还没有统一的、权威的、标准的定义,但遵循数学学科特点,依据Reitman理论,一线教师将那些初始状态(条件、信息)、目标状态(确定、开放)和解决问题策略(方法、途径)等因素中至少有一项没有明确界定的数学试题称为结构不良试题.据此可知,本题属于典型的三角知识模块下的初始状态不够清晰的结构不良试题.
3 深入剖析条件
波利亚在名著《怎样解题》中提出解题四部曲:剖析条件、拟定计划、实施计划、回顾反思.由于本题初始状态中有三个选项供选择,因此深入剖析条件,厘清条件之间的关系,对最终解决问题具有决定性作用.
(1)逐个条件单独分析
仅从单个条件看,条件①:tanB=2tanC中仅仅涉及角,由此联想到遇切化弦,或直线斜率,或构造直角三角形;条件②:3b2-a2=12中仅仅涉及边且出现边的平方,由此联想到余弦定理;条件③:bcosC=2ccosB中既有角又有边,由此联想到利用余弦定理转化为边,或正弦定理转化为角,或应用射影定理.
(2)全部条件整体分析
既然有三个条件供选择,哪三个条件之间是否有关联呢?
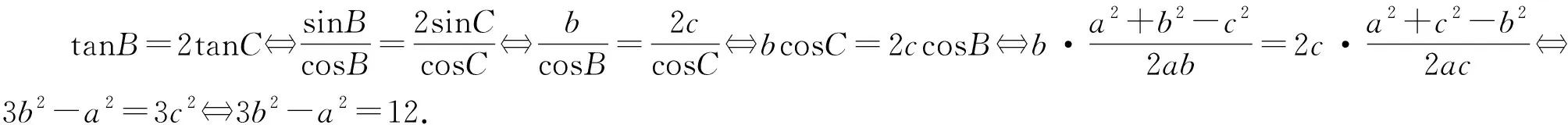
由此说明条件①、②与③相互等价,从而,无论选择条件①、②还是③,△ABC的面积的最大值都是相同的.
(3)待求结论条件分析

本题关键在于将已知条件①,或②,或③,结合公共条件c=2,积极地向上述三角形面积公式“靠近”,寻觅已知条件与求解结论对接的“桥梁”,形成解决问题的“抓手”,进而借助数学方法(如配方、基本不等式等)求出最值,其本质就是构建数学模型的过程.
4 立足核心素养的解题教学
尽管条件①、②与③相互等价,但仍有不少考生难以入手,这是导致考生放弃的主要原因.解题教学中该如何决策呢?
(1)侧重代数(运算)视角——以条件②为“抓手”,着力培养数学运算素养
倘若从条件②出发,可得以下构思过程:

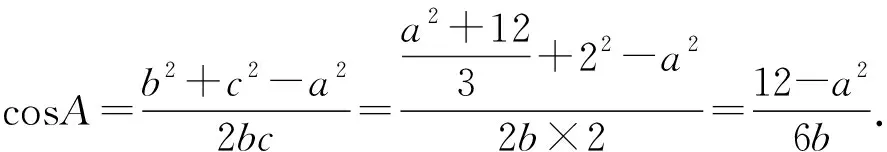
既然可以从cosA入手,是否也可以从cosB或cosC入手呢?其实,类似于上述解法1与解法2,针对角B、角C分别得到解法3、解法4及解法5、解法6(过程略).

评注:以条件②为抓手,属于典型的代数解法,有利于培养数学运算素养.数学运算素养的核心就是理解运算对象、掌握运算法则、探究运算方向、选择运算方法、设计运算程序、求得运算结果.其中,解法1与2、解法3与4、解法5与6本质相同(即运算对象),掌握运算法则(面积公式)、探究运算方向(瞄准面积公式)、选择运算方法(代入、配方、基本不等式)、设计运算程序(先求余弦值,再求正弦值)、求得运算结果,但是仔细体会却有细微差异,主要表现为用选择(1)还是选择(2)代入,导致运算步骤与运算量不同.至于解法7,如果直接全部展开,运算量很大,于是将l与l-c、l-a与l-b两两结合,并借助平方差公式优化运算,这正是培养运算素养的关键所在.教学中应该将运算过程详细展示,必要时还要给出特写“镜头”,将培养运算素养的举措落到实处.
(2)侧重几何(图形)视角——以条件①为抓手,着力培养直观想象素养
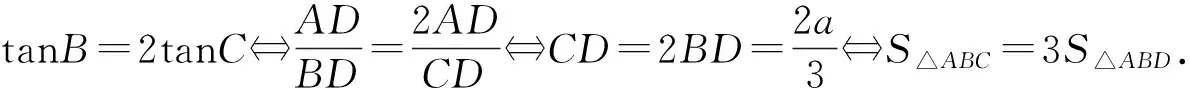



评注:直观想象就是借助于见到的或想象的几何图形进行直观感知、整体把握的能力.克莱因认为:“数学不是依靠在逻辑上,而是依靠在正确的直观上.”史宁中指出,在大多数情况下,数学的结果是“看”出来,而不是“证”出来的.就本题而言,条件①:tanB=2tanC通过构造三角形,将三角(代数)问题转为具有几何直观的图形,实现由数思形、以数构形,不仅大大简化了运算,而且凸显问题的本质,即上述解法8、解法9及解法10的实质就是对于斜边为定值的直角三角形,当且仅当等腰三角形时,直角三角形面积最大.
(3)侧重解析(数形结合)视角——以条件①、②为抓手,着力培养逻辑推理素养
数学是研究数与形的科学,因此数形结合是解决数学问题的重要思想方法,其中最为常见的就是建立适当坐标系,将图形中的元素用坐标来表示,进而转化为代数运算.


评注:在解析视角下,通过推理及坐标运算,纯代数问题转化为具有几何意义的相关问题,这正是逻辑推理素养的体现.逻辑推理素养是描述思维品质中深刻性的重要指标之一.数学解题教学中的逻辑推理是指依据一些事实和命题,按照数学逻辑规则得到新命题的思维过程.逻辑推理能够揭示出隐藏在情境中的事物或现象背后的本质规律,并预见事物或现象的发展进程.上述解法11与解法12,不仅简捷地求出了△ABC的面积的最大值,而且发现了本质规律:由于c=2,即|AB|=2,满足条件的动点C的轨迹是一个定圆.
5 结构不良试题的解题教学是落实核心素养的良机
本题是一道典型的结构不良试题,尽管条件①、②与③相互等价,但是条件①、②与③的功能与侧重点不尽相同.其中,条件②侧重于代数视角,这就是上述解法1—解法7的由来;条件①侧重于几何视角,这就是上述解法8—解法10的由来;同时条件①与条件②兼具数形双重“身份”,这就是上述解法11、解法12的由来.命题专家精心设计三个选项,意在诠释《新课标》基本理念:以学生发展为本,落实立德树人根本任务,面向全体学生,人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.
事实上,条件③:bcosC=2ccosB⟺sinBcosC=2sinCcosB.倘若从条件③出发,还可以得到以下赏心悦目的构思过程(解法13、解法14),极大激发学生学习数学的积极性.不仅学会了知识与技能,而且展示了过程与方法,更加凸显了情感态度价值观的培养.
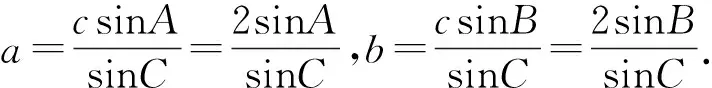

相对于初始条件明晰、目标设置明确、解题方法明显的结构良好试题,结构不良试题具有难度高、跨度大、视角广、路径多的特点.教师在解题教学过程中,根据具体问题,引领学生多角度分析、多途径思考,提出多种解决方案,达到优化学生数学思维的系统性、灵活性、深刻性与创造性.
林崇德教授把学生在接受相应学段的教育过程中,逐步形成的适合个人终身发展和社会发展需要的必备品格和关键能力界定为核心素养.依据数学学科特征,《新课标》明确提出六大数学核心素养:数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析.它们之间既有区别又有联系,既各有侧重,又形成和谐统一,你中有我,我中有你,形成和谐有机整体.比如,在涉及概率统计模块的结构不良试题,主要培养数学抽象、数学建模、数据分析素养;在涉及立体几何模块知识的结构不良试题,主要培养直观想象、逻辑推理素养、数学运算素养.数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的关键能力与思维品质.在数学教学活动(概念传授、解题教学)中,持之以恒地重视核心素养,树立优化核心素养的意识,落实培养核心素养的措施,创设合适的教学情景,感悟数学的思想方法,积累数学思维的经验,在潜移默化中形成和发展核心素养.

