通过一道试题研究与抛物线切线相关的性质

广东省佛山市顺德区李伟强职业技术学校 (528300) 王晓敏

抛物线具有丰富的几何性质，如果在解题的过程中能灵活地运用相关性质，那么在解题的过程中就可以起到事半功倍的效果.笔者在研究一道抛物线相关问题时，就从中总结了多条相关性质，并发现其中隐含了一个“阿基米德三角形”.

一、题目及分析

如图1，过点Q(-2,m)作抛物线y2=8x的两条切线，切点分别为A，B，直线QA，QB分别交y轴于C，D两点，若S△QAB=6S△QCD，求m的值.

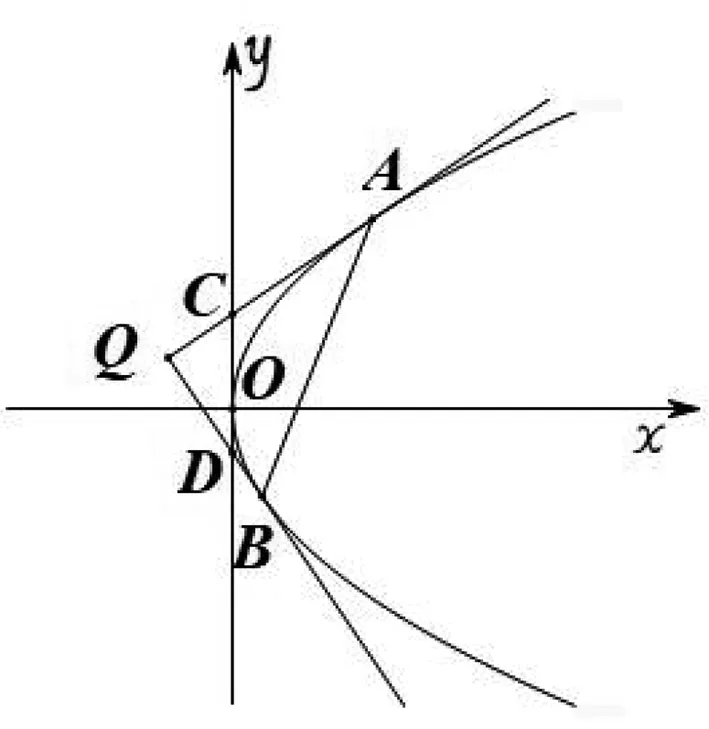
图1

分析：观察可知，点Q位于抛物线的准线，过该点作抛物线切线所构成的切点弦[1]必经过抛物线的焦点.为此，我们可以利用焦点弦这一信息来计算△QAB的面积.为了计算△QCD的面积，还需考虑点C，D所满足的几何关系.

二、解法呈现

为了解决上述问题，现将解题过程分解为如下几个环节.

环节一：切点弦AB过焦点F

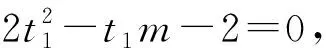
解法二：(以极点极线[2]的意义求解)根据极点极线的几何意义可得以点Q为极点，对应的极线为切点弦所在的直线，即直线AB.根据极点极线的代数意义可得，当点Q的坐标为(-2,m)时，其关于抛物线y2=8x的极线方程为AB:my=4(x-2)，即可得该方程恒过抛物线的焦点(2,0).

环节二：计算△QAB的面积

根据上述证明过程可知直线AB恒过焦点(2,0)，可设直线方程为AB:x=ty+2.设该直线对应的极点为T(x0,y0)，利用极点极线的代数意义可得直线AB的方程应为AB:y0y=4(x+x0).根据两直线方程相同，可得x0=-2，y0=4t，结合点Q的坐标可得m=4t.

说明：该表达的意义在于以直线AB为基本量，能极大地简化后续的运算以及证明.

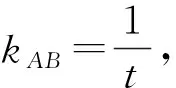
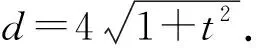
环节三：关于点C，D的几何性质

如图2，分别过点A，B，F作准线l的垂线，垂足为M，N，F′.根据抛物线的光学性质，切线QA为∠MAF的角平分线，易知△MAF为等腰三角形，故直线QA经过MF的中点.考虑△MFF′，MF与y轴的交点即为MF的中点.综上可得：QA与y轴的交点C为MF的中点.同理，QB与y轴的交点D为NF的中点(证明过程详见后文).

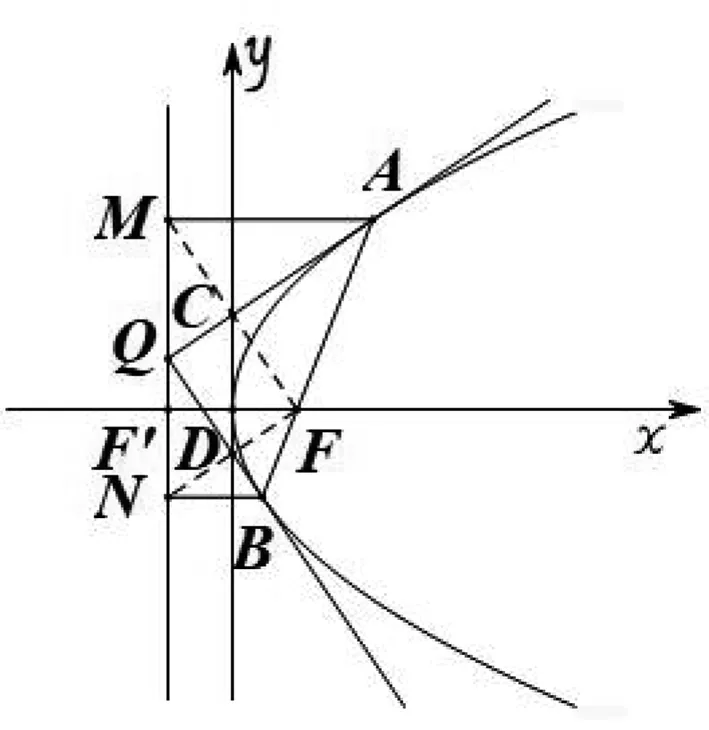
图2

在直角梯形AMNB中，可得∠MAB+∠NBA=180°，从而AQ⊥BQ，即四边形QDFC为矩形.

环节四：计算△QCD的面积

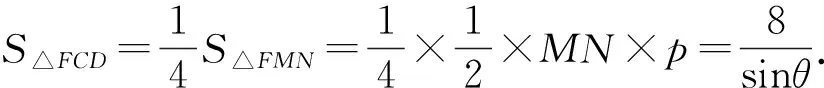
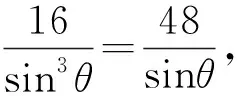
三、总结试题所蕴含的一般性质

在上述解题过程中，出现了很多与抛物线相关的几何性质，现对出现的性质进行梳理.

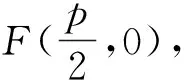
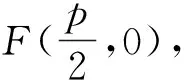
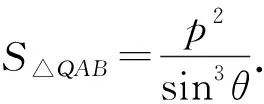
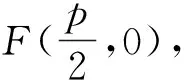
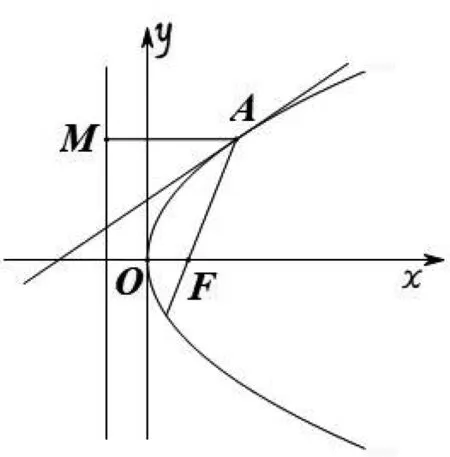
图3

性质3 如图4，已知抛物线y2=2px(p>0)，分别过点A，作准线l的垂线，垂足为M，N，过点A，B作抛物线的切线lA，lB交于点Q，则有AQ⊥BQ，即四边形QDFC为矩形.

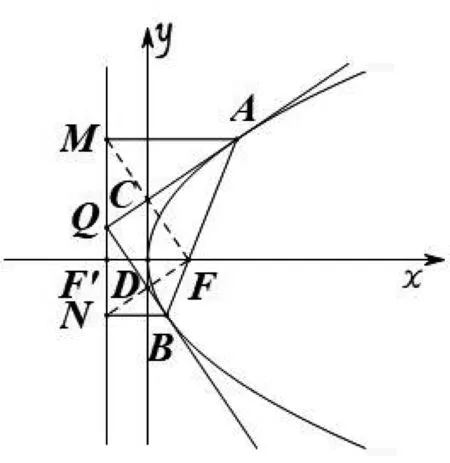
图4

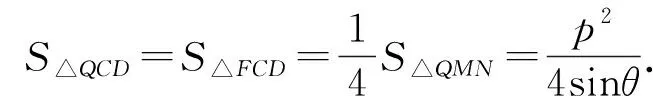
只要将上述证明过程中的问题进行一般化处理即可得到上述性质的证明，本文不再赘述，现仅介绍一下性质2的证明过程.

关于光学性质的证明，可以通过角平分线的性质以及切线的极限定义进行几何方面的证明，也可利用代数方程进行证明.本文仅介绍第二种证明思路.

证明：如图5，设点A的坐标为(x1,y1)，根据极点极线的结论过点A的切线方程为lA:y1y=p(x+x1).该直线与x轴的交点为T(0,-x1)，结合抛物线的定义可得TF=AF，即可得△ATF为等腰三角形，从而即可得切线l为∠MAF的角平分线.

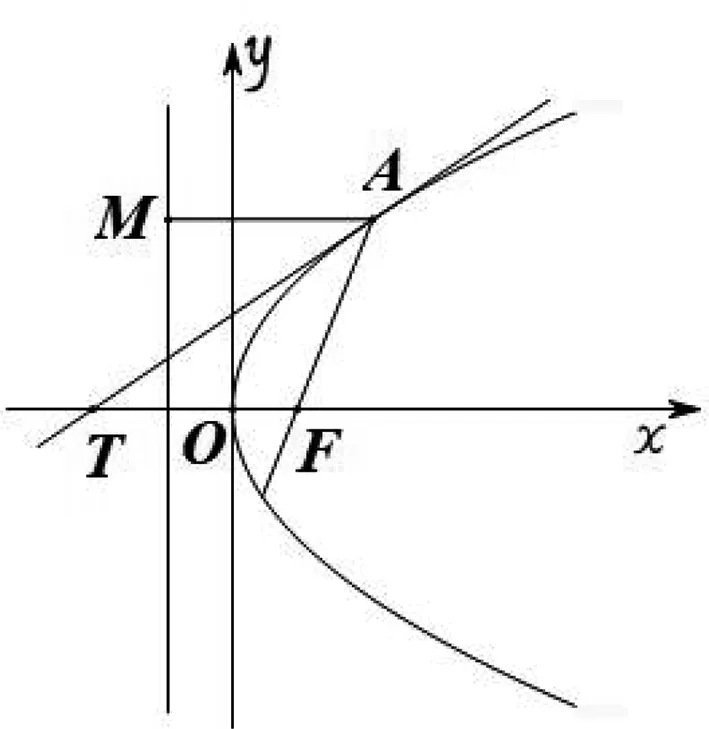
图5