精选高考试题 创设探究情境 落实引导教学*

江苏省泗洪姜堰高级中学 (223900) 程 坚 王开瑞

高考评价体系主要有“一核”“四层”“四翼”三部分内容组成，它是高考命题、评价与改革的理论基础，也是教育教学的实践指南.将优秀的高考试题创新、高效地应用于中学课堂教学，充分发挥高考试题的潜在价值，是高考引导教学的现实要求.本文结合一道典型的高考试题，创设恰当的教学环境，研究其教育教学价值.

一、试题及其分析

(1)求C的方程；

评析：第(1)问要求学生理解双曲线的定义和标准方程，理解曲线和方程的对应关系，能利用待定系数法求双曲线的标准方程.

第(2)问考查直线与双曲线的位置关系，考查直线参数方程的运用.考虑到直线的参数方程在新课标中不作要求，要求学生选用直线的点斜式方程，并灵活地选择恰当的方法求解距离的乘积，然后利用数的对称轮换简化求解过程，考查运算求解能力和理性思维能力.

二、创设探究情境 落实引导教学

问题探究1：在学生求解问题(2)时，引导学生从特殊入手，猜想、探究直线AB的斜率与直线PQ的斜率之和.

问题探究2：请选择恰当的直线方程，并利用恰当的方法求出|TA|·|TB|,|TP|·|TQ|.

设计意图：由于在新课标中，直线的参数方程不作要求，因此首选直线的点斜式方程，但是直线的参数方程特别简单，对优秀的学生可以补充要求；求TA|·|TB|时，可以利用两点间的距离公式，也可以利用弦长公式，还可以利用平面向量的数量积，其中利用平面向量的数量积综合性强、过程简单、对学生的素质要求高；求|TP|·|TQ时，可以利用同理可得再求解一遍，但是利用数的对称轮换求解更简单，他对培养学生数的对称轮换思想有着独特而重要的作用.教学时，先提出这样的问题，让学生思考、讨论、比较，然后选择最简单的方法求解，这是解题教学应该关注的问题，也是利用过程教学提升运算求解能力和理性思维能力的关键.

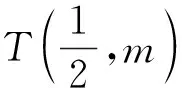
问题探究4：将上面的问题一般化，能提出怎样的问题，怎么求解？

设计意图：创设数学情境，培养学生提出问题、分析解决的能力.将这个问题一般化，有下面的问题：

在平面直角坐标系xOy中，点T在直线x=m(或y=n)上，过T的两条直线分别交曲线C：ax2+by2=c(a≠b)于A,B两点和P,Q两点，且|TA|·|TB|=|TP|·|TQ|，求直线AB的斜率与直线PQ的斜率之和.

解：设T(m,n)，直线AB的参数方程为

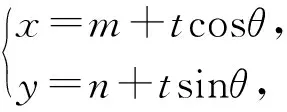
当a=b时，曲线C：ax2+by2=c表示圆的方程，由相交弦定理和切割线定理知|TA|·|TB|是定值，由|TA|·|TB|=|TP|·|TQ|不能推出直线的斜率之和为0.此外，利用平移变换可以进一步推广，对于对称轴和坐标轴平行的椭圆、双曲线、抛物线，这个结论都成立.