运用GeoGebra软件助力数学实验探究教学*——以一类解析几何定点问题为例

广东省中山市濠头中学 (528437) 闫 伟

《普通高中数学课程标准(2017年版)》要求注重培养学生在学习上的自主探究，鼓励学生运用信息技术学习、探索和解决数学问题[1].为了让学生真正参与到课堂教学中，经历主动获取知识的过程，提升学生的直观想象能力，笔者以一节高三数学复习课中有关椭圆的定点问题为例，说明运用GeoGebra平台开展实验探究的教学价值.

1 问题的提出

图1

问题4 若将椭圆换成双曲线，上述结论是否还成立呢？若换成抛物线，结果又会如何？

问题5 若点F不在对称轴上，即是椭圆内其他点，根据上述条件作出直线BD，我们又会得出什么结论？

2 基于GeoGebra平台的探究

大家对上面几个问题都惊叹不已，一个题目能衍生出这么多新问题，这些结论是否都成立呢？带着诸多疑惑和兴奋，师生开始了实验探究之旅.问题2～问题5将椭圆和点F及对应的直线一般化，因涉及的运算和直线BD的直线方程较复杂，判断上述结论成立与否有有较大的难度，故笔者借助GeoGebra平台进行探究，通过实验演示观察该结论是否成立，同时为接下来的代数证明提供更加直观的思路支持[3].

实验1 (1) 在GeoGebra绘图区中先设置两个“滑动条”控制变量a,b，输入x^2/a^2+y^2/b^2=1得到一个椭圆c.(2)输入框中输入焦点[c]，得到椭圆的右焦点F.(3)使用“滑动条”创设变量m,作出过点F的直线x=my+c，利用交点工具确定A,B.(4)在输入框中输入x=a^2/sqrt(a^2-b^2)得到直线l，作出直线l与x轴的交点H.(5)过A点作直线l的垂线交直线l为D点.(6)作出直线BD，借助GeoGebra中的“追踪”功能显示直线BD的轨迹，拖动“滑动条”的变量m发现直线BD恒过x轴上的一个定点(图2).

图2

实验2 (1)按照上述实验操作步骤修改第(2)、第(3)步：去掉右焦点，再通过“滑动条”设置一个变量t，作出点F(t,0)，并作出过点F的直线x=my+t.(2)第(4)步变为：在输入框中输入x=a^2/t得到直线l，作出直线l与x轴的交点H.(3)其他步骤不变.(4)先改变F点的位置，再拖动“滑动条”的变量m，发现直线BD仍恒过x轴上的一个定点(图3)，而且定点的位置随F点的变化而改变，且始终是直线l与x轴的交点H与F点的中点.当改变椭圆的方程时，师生发现仍然有同样的结论.

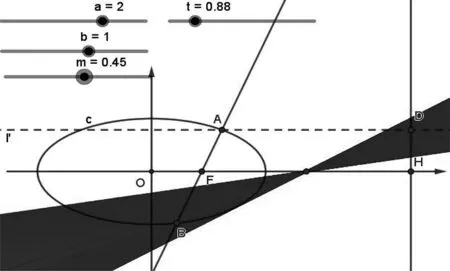
图3

3 推广结论 揭示本质

根据以上实验的探究结果，师生可以直观认识到上述问题的结论都能成立，于是可以将上述试题推广到一般情形.

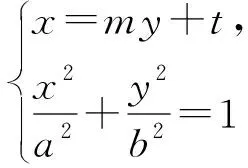
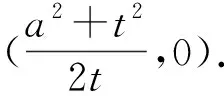
当t=c时，F是右焦点，结论1是结论2的特例；若将椭圆换成双曲线，利用GeoGebra软件继续探究，经同样的实验操作，发现直线仍恒过定点，如图4所示，从而有如下结论：

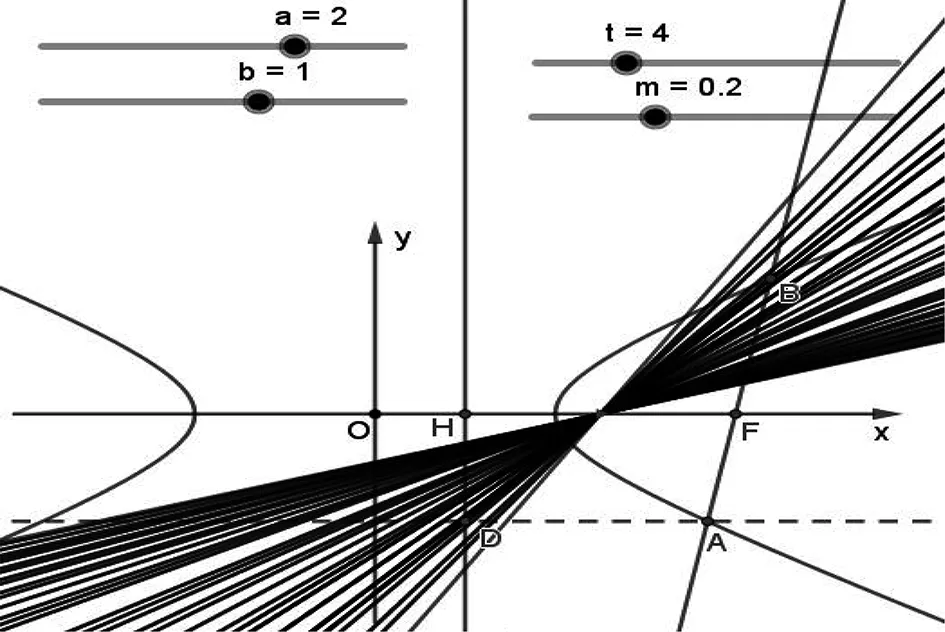
图4

结论3的证明和结论2的过程相仿，此处不再赘述；将椭圆换成抛物线(图5)，师生有类似的结论：

图5

结论4 过抛物线C:y2=2px(p>0)对称轴点F(t,0)(t>0)且斜率不为零的直线与抛物线交于A,B两点，直线l:x=-t与x轴交于点H，过点A作AD⊥l，垂足为D，则直线BD恒过定点(0,0).

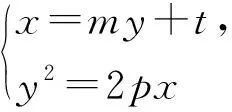
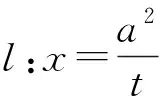
图6

结论7 过抛物线C:y2=2px(p>0)内侧一点F(x0,y0)的直线与抛物线交于A,B两点，过点F作直线l:p(x+x0)-yy0=0的垂线，垂足为H点，过点A作AD⊥l，垂足为D，则直线BD恒过线段FH的中点.

根据极点和极线的性质，师生可以将结论5～结论7统一概括为：

结论8 已知圆锥曲线C和异于曲线中心且不在曲线C上的一点F，点F关于曲线C的极线为l，过点F的直线与曲线交于A,B两点，分别过点F、点A作直线l的垂线，垂足分别为H、D两点，则直线BD恒过线段FH的中点.

4 探后反思 引领教学

《普通高中数学课程标准(2017年版)》明确指出，“提升信息技术的使用能力，通过信息技术与课程的深度融合以及课程资源开发的多样化实现”. 这就需要合理运用信息技术，以此提高数学教学的有效性.在教学过程中，把信息技术与数学课程进行有效的整合，不仅能够实现数学对象的多元表征(数字、表达式、图形等)，而且会使抽象的数学知识变得形象直观，有助于培养学生直观想象等核心素养[1].

在“互联网+”时代，信息技术的应用正在对数学教学产生深远的影响，如何使数学教学适应时代的发展，已经成为新时代教师所关注的焦点. 在本文的实验探究中，运用GeoGebra技术制作椭圆模型，再通过控制变量不断改变动直线和方程参数来演示图形变化过程，让学生观察所求点的轨迹的运动情况，进而将实验结果拓展到曲线的统一结论，不仅为学生理解试题本质创设教学情境，而且为学生探索试题规律启发思维，为学生解决数学问题提供直观形象.GeoGebra平台技术的可视化实验让学生有机会亲身体验探究问题背后的规律，还能“看透”深层次的数学本质，让学生主动发现问题，解决问题，发现和体会数学的美，充分调动了学生的学习兴趣和积极性,有助于学生树立学好数学的信心，亦有利于培养学生逻辑思维、空间想象、探究学习、创新和实践等能力, 从而促进学生数学学科素养的提升[2].