基于抽象素养培养的变式教学探究
——以2018年高考全国卷Ⅰ理科第16题为例
2022-07-08 00:53324022浙江省衢州第三中学汤小青
中学数学 2022年4期
324022 浙江省衢州第三中学 汤小青 陈 旭
变式教学的教学策略包括概念性变式和过程性变式.
概念性变式是指构建合适的变异维度,让学生体验学习对象的关键方面,形成对概念的本质理解.
过程性变式旨在提供适当的铺垫,帮助学生形成学习对象与已有知识的内在、合理的联系.
两种变式策略共存互补、相互促进,分别在不同情境、不同阶段发挥作用.
数学抽象素养的形成包含概念、规则的获得,命题和模型的提出,知识结构和体系的形成.
通过概念性变式教学,学生能从多角度体验学习对象的数学本质,更好地获得概念和规则;通过过程性变式,学生能更合理地构建知识的内部联系,形成知识结构和体系.
因此,变式教学的开展更有利于抽象素养在课堂教学中的落地生根.
笔者以2018年高考全国卷Ⅰ理科第16题为例,从变式教学层面进行抽象素养培养的探究.
一、 原题再现
原题
(2018全国卷Ⅰ理-16) 已知函数f
(x
)=2sinx
+sin2x
,则f
(x
)的最小值为________.
二、 变式教学设计
为便于不等式的使用,将原题变为以下变式.
变式
已知函数f
(x
)=2sinx
+sin2x
,则f
(x
)的最大值为________.
(一)单调性开路
变式解法1:
函数f
(x
)=2sinx
+sin2x
周期为2π,故只需求解一个周期内的最大值即可.
求导可得f
′(x
)=2cosx
+2cos(2x
)=2cosx
+4cosx
-2=2(cosx
+1)(2cosx
-1).
故当时,f
′(x
)≥0;当时,f
′(x
)≤0.
故函数变式解法2:
由万能公式可得故y
=f
(x
)=2sinx
+sin2x
=令则那么则函数y
=g
(t
)在区间上y
′<0,在区间上y
′>0.
所以时,函数的最大值为变式1
求函数的最大值.
解法1:
换元,令则后续参见变式解法1.
解法2:
直接求导进行求解,后续解答过程略.
变式2
求函数的最大值.
变式2解法与变式1类似,此处略.
设计意图:
利用所学知识寻求普适性的方法是解题教学的首要任务.
利用导数求解函数单调性,进而解决最值问题,是求解所有可导函数最值问题的通法.
从最值的层面更好地构建导数在函数问题中的价值.
(二)应用不等式初探
变式解法3:
f
(x
)=2sinx
+sin2x
=2sinx
·(1+cosx
),则f
(x
)=4sinx
,那么结合基本不等式可得当3-3cosx
=1+cosx
,即时取等号),所以当时取得).
或者结合那么可以化为
变式3
求函数的最大值.
解法1:
换元,令则y
=sinθ
cosθ
,利用类似变式解法3的方法处理.
解法2:
利用基本不等式求解,当时取得最大值).
变式4
求函数的最大值.
解法1:
换元,令则y
=sinθ
cosθ.
解法2:
利用基本不等式求解,当时取得最大值).
设计意图:
从基本不等式的角度,利用四阶基本不等式构造和为定值,进而求得乘积的最大值.
利用三角恒等变换将题中和的形式转化为乘积形式,再结合不等式进行处理,理顺了三角函数中的不等式使用思路.
(三)应用不等式再探
变式解法4:
f
(x
)=4第一个柯西不等式取得等号的条件和第二个二次型函数最值取得等号的条件相同,为
变式解法
当时取得等号).
变式5
求函数y
=f
(x
)=sinx
+sin2x
+sin3x
的最值.
解:
f
(x
)=sinx
+sin2x
+sin3x
=2(sinx
cosx
(柯西不等式等号和二次函数最大值条件一致,即设计意图:
从乘积和的结构出发,结合柯西不等式进行系数的构造,使得前后的等号一致;从乘积的形式,分别构造基本不等式,进行系数的构造使得前后的等号一致.
从结构出发,发现不同的思考角度,多角度揭示问题的本质.
进一步强化利用不等式解决最值问题的基本思路.
(四)数形结合显威
变式解法6:
f
(x
)=2sinx
+sin2x
=2sinx
·(1+cosx
),P
(cosθ
+1,sinθ
)为C
:+y
=1上的点,只需求x
·y
=c
的最大值.
由图1,令则h
(x
)与圆相切时c
最大.P
点切线的斜率为所以解得舍去,此时故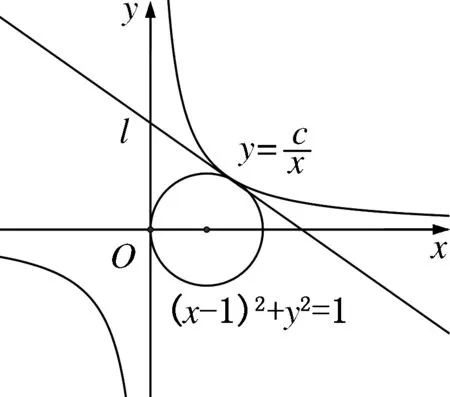
图1 相切求最值
变式6
求函数y
=f
(x
)=sin(2x
)+2sinx
+2cosx
+2的最大值.
解:
f
(x
)=sin(2x
)+2sinx
+2cosx
+2=2(sinx
+1)·(cosx
+1),P
(cosθ
+1,sinθ
+1)为C
:=1上的点,求x
·y
=c
的最大值.
令则h
(x
)与圆相切时c
最大,P
点(cosθ
+1,sinθ
+1)切线的斜率为所以解得(cosθ
=-1舍去),故变式解法7:
y
=f
(x
)=2sinx
+sin2x
=2sinx
·(1+cosx
),构造单位圆的内切等腰三角形,如图2,设∠BOD
=x
,则DO
=cosx
,CD
=1+cosx
,BD
=sinx
,AB
=2sinx
,所以S
△=sinx
(1+cosx
),所以要求函数f
(x
)=2sinx
+sin2x
的最大值等价于求S
△面积的最大值.
设∠COB
=α
,∠AOB
=β
,∠AOC
=γ
,则由琴生不等式可得当时取等号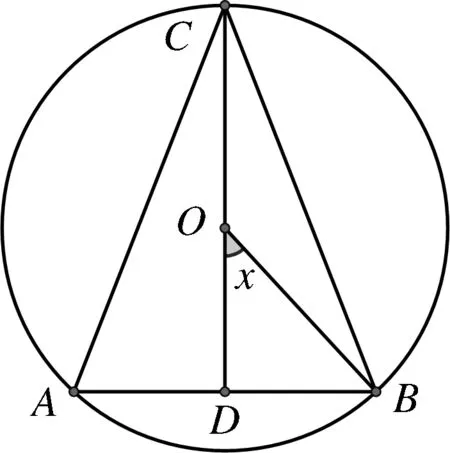
图2
设计意图:
此题利用“sinθ
(1+cosθ
)”构造圆C
:+y
=1,利用“2sinx
(1+cosx
)”构造单位圆的内切三角形的面积.
以三角函数的特性为媒介,从图形角度诠释三角表达的内涵,利用图形转化解题方向.
数形结合是高中数学的重要思维,通过多角度探究,学生经历多维度思考,提升数形结合的思维层次.
(五)高观点立意
变式解法8:
因为y
=sinx
在为上凸函数,由琴生不等式可得y
=f
(x
)=2sinx
+sin2x
=sinx
+sinx
+sin2x
=sin(π-x
)+sin(π-x
)即当时取等号).
当时,故函数f
(x
)=2sinx
+sin2x
在区间(0,π)上最大值为函数f
(x
)=2sinx
+sin2x
在区间(0,π)上的最小值必然大于-1,因为函数f
(x
)=2sinx
+sin2x
是奇函数,所以在(-π,0)上的最大值小于由周期性可得函数f
(x
)=2sinx
+sin2x
的最大值为变式7
求函数的最大值.
解:
因为y
=sinx
在为上凸函数,由琴生不等式可得即当时取等号).
变式8
求函数的最大值.
解:
因为y
=sinx
在为上凸函数,由琴生不等式可得即时取等号).
设计意图:
2019年人教版高中数学新教材必修一第三章复习参考题中就有“求证:若g
(x
)=x
+ax
+b
,则这一与函数凹凸性紧密结合的题型.
从函数的凹凸性到琴生不等式,利用琴生不等式解决函数的最值问题,为函数最值的知识结构增加了重要的组成部分,也可将琴生不等式的使用条件一般化为“y
=f
(x
)=a
sin(bx
)+c
sin(dx
),其中ab
=cd
”.
三、 反思与总结
(一)通过变式教学设计完善知识结构,形成知识体系
函数最值问题的知识结构和体系较为复杂,结合三角公式、三角函数可以实现形式的多变性,在多种形式的基础上融合多种方法,进而帮助学生更好地抽象出函数最值问题的知识结构和体系.
从通法的角度利用导数研究单调性求最值,结合万能公式,再利用求导求最值;将基本不等式、柯西不等式的形式特点和三角函数的公式变形进行有机结合,让结构的形式和问题的实质相融合;利用问题的结构特征构造反比例函数和圆的相切、构造单位圆的内切三角形面积,让抽象的代数与直观的图形相融合;从函数的凹凸性观点,进一步揭示问题的实质.
(二)通过变式教学设计一题多解,抽象出问题的实质,提升思维品阶
数学核心素养水平的提升,思维能力的进阶,是一个有序的过程.
通过合理的变式教学设计、多维度逐层深入的变式,学生经历由通性通法到多种不等式探究、再到数形结合、最后在高观点下立意的探究过程,在逐层深入的过程中逐步揭开问题的实质,不断提升数学核心素养水平,发展高阶思维.
(三)通过变式教学设计多题一解,抽象方法的内涵,形成一般性结论
在变式教学设计中,每一维度都设计多个变式,实现多题一解,使学生多角度认知方法,形成一般性的结论.
猜你喜欢
现代职业教育·高职高专(2018年11期)2018-06-11
中学数学杂志(初中版)(2017年2期)2017-05-09
中学课程资源(2017年1期)2017-02-18
中学课程资源(2017年1期)2017-02-18
求学·理科版(2016年11期)2016-11-29
数理化学习·初中版(2009年7期)2009-11-23
青年文摘·上半月(1985年3期)1985-11-01

