“画”说解决问题 构建数学模型
——以《植树问题》为例
文 管茂堂
植树问题是一类典型的应用问题,是一种应用广泛的数学模型。植树问题的数量关系比较复杂,解决问题的基础是理解除法的意义,核心是正确分析段数与棵数之间的关系。学生在解决植树问题时,常常难以进行有效的数量推理,本教学中是借助图画突破这个难点,引导学生认识数量关系,选择正确的计算方法。画图既是解决问题的手段,也是实现教学目标的抓手。
【教学过程】
一、画图初建数学模型
师:今天我们要学习植树问题,关于植树问题,你们有什么问题要问吗?
生:什么是植树问题?
生:为什么要学习植树问题?
出示:在全长100米的小路一边植树,每隔5米栽一棵(两端都栽)。一共要栽多少棵树?
1.数据分析,猜测结果。
师:读一读,在题中你读到哪些信息?谁来说一说?
生:100米是一共的长度,5米是两棵树之间的距离。
生:一边指的是路的左边或者右边。
生:两端都栽是起点和终点都要种。
师:猜测一下,你觉得要种多少棵树,怎样列式?
生1:100÷5=20(棵)。
生2:100÷5+1=21(棵)。
生3:100÷5+2=22(棵)。
师:这些方法有什么相同的地方,有什么不同的地方?
生:相同的地方都用100除以5,不同的地方有的不加、有的加1、有的加2。
2.化繁为简,画图验证。
师:到底是+1?+2?还是不加呢?我们可以用什么方法来验证?
生:可以画线段图来验证。
师:你准备怎样画呢?
生:我们用一条线段来表示100米,每隔5米种一棵,照这样画下去。
师:其他同学怎么看?你们有什么好的建议吗?
生:我们可以先想20米长的路种树是什么情况。
师:这个建议真不错。当我们用大的数据来寻找规律比较麻烦时,可以考虑先用小的数据找找规律,再推广到大数据中去。我们先截取100米中的一小段来研究,这种方法能够——化繁为简。
师:请各自在作业纸上画图,看一看,你有什么发现?
师:这是第一位同学的画法,你们怎么评价?

生:这幅图与条件不符,没有平均分完,总长与段数不符合。
生:总长20米,5米种一棵,种那么多肯定超过20米了。
师:这是第二位同学的画法,你们怎么评价?

生:这也不对,图中有5个5米,总长应该是5×5=25米了。
师:每隔5米种一棵,现在这幅图画的总长是多少米?怎么修改?
生:去掉一小段。
生:保留四段。
师:(画对的学生)你是怎么想的,怎么画的?
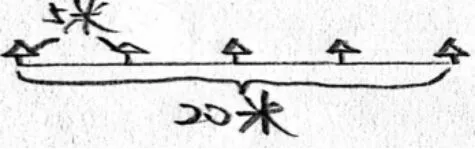
生:总共20米,5米分一段,所以一共只能分成4段。
师:那树有几棵呢?
生:5棵。
师:怎么得到的?
生:数出来的。
3.一一对应,分析规律。
生:也可以分析出来,棵数比段数多1棵。
师:你是怎么想的?
生:第一棵树对应第一段,第二棵树对应第二段……最后一棵没有对应的段,就是多出的那棵。
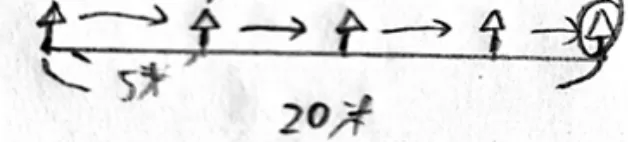
师:用对应的方法思考问题,真好。谁听懂了?
师:在画图的基础上,你能列式来表示这个分析的过程吗?
生:20÷5=4(段),4+1=5(棵)。
生:20÷5+1=5(棵)。
师:这两个算式都能看懂的同学请举手。谁来试试解释算式的意义?
生:20除以5,表示把20米5米5米地分,可以分4次,就是4段路。4+1是因为树的棵数比路的段数还要多1,最后1棵树没有对应的路段。
4.反复验证,总结规律。
师:我们得到了棵数比段数多1或者说段数比棵数少1的结论。这个规律是不是普遍存在?可以推广到更长的距离中吗?
师:大家各自截取一段路,再画一幅图。看看是否还是这样的规律?
出示学生画的图:
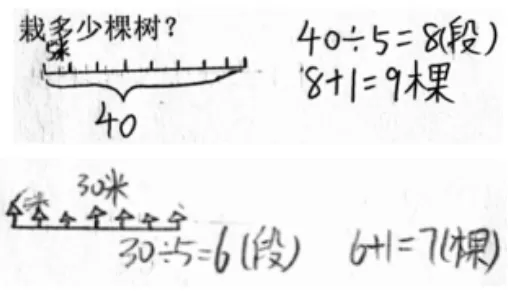
生:其实不用画图也可以。现在的段数比棵数少1,如果再增加一段,就要再种一棵树,这样一直增加下去,段数始终比棵数少1。
生:我们还可以这样想,无论你画多少,第一棵对应第一段,倒数第二棵对应最后一段,最后还有一棵,因此,段数总比棵数少1。
师:我们通过画图发现了规律,用推理解释了规律,现在我们可以得到的一个重要的结论——
生:段数+1=棵数。
师:现在你知道前面的三种算法,哪一种是对的?
师:如果列出一个综合算式,怎么列?
生:100÷5+1=21(棵)。
师:表示什么意思?
生:总长÷间距+1=棵数。
师:类似的问题,如果小路长1000米,两端都种,可以种几棵?
生:1000÷5+1=201(棵)。
师:我们再来看前面交流的另外两种算法,一种是不加,一种是加2,你觉得题目怎么改动一下,这样算就可以?
生:也可以第一棵不要种,只要一端种树一端不种就可以了。
师:你们的意思是,一端不种一端种的情况下,段数=棵数。
师:那有没有什么情况下,棵数等于段数加2呢?
生:没有,棵数不可能比段数多2。
生:棵数可能比段数少1,就是两端都不种的情况。
小结:植树方式不同,棵数与段数之间的关系就不一样。
【设计意图:画图发现数量之间的关系是解决问题的关键。让学生独立思考,通过画图分析数量关系、利用关系,把求棵数的问题转化为求段数的问题。求段数的方法是唯一的,即除法中包含除的意义。学生经历了观察现象、形成猜想、推理验证、结论变式、解决问题的过程,这种过程性的思维经验是可以迁移的。】
二、运用数学模型画图解决问题
出示:一盒9响鞭炮,从听到第一声爆炸声开始计时,到第二声响起时,经过2秒钟。当听到最后一声响起时,一共经过几秒钟?
师:老师带领大家做一个小游戏。对着钟面,当秒针走到1时,拍一下掌,表示鞭炮的响声;5秒后走到2时,再拍一下掌;走到3时……走到9时,拍最后一下。现在,你能把刚才玩的放鞭炮游戏画下来吗?
生:我是从钟面的1开始,到9结束,每个数字代表一次响声。
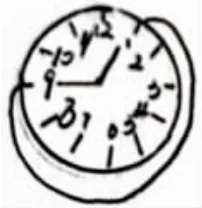
生:我把钟面拉直后,从1开始,数到9,一共隔了8个5秒。

生:我发现数字相当于树,9个数字就是9棵树,一共有8段,每段是5秒,所以一共是40秒。

生:我是用方程来做的。我把总时间当作总长,每个数字当作树,5秒当作间隔长。根据总长÷间距+1=棵数,可以得出:总秒÷间距秒+1=响数。列出方程:x÷5+1=9。
师:那你们知道生活中还有哪些也是植树问题吗?
生:敲钟也是植树问题。
生:还有排队问题,人就是树,人与人之间的距离就是间隔长。
【设计意图:引导学生结合画图,在图中找出鞭炮问题和植树问题的关联:声音是“树”,两响之间的间隔时间就是间隔长。进一步让学生举例生活中的植树问题,如装路灯、排队、敲钟等,真正建立数学模型思想。】
应用问题的核心是分析数量关系。本课教学,通过画图的活动,引导学生利用几何直观分析和概括数量之间的关系,有效解决问题。通过画图,把抽象的问题直观化,隐蔽的关系显性化,让更多学生更加主动地参与到学习活动中,不仅对植树问题生成更深层次的数学理解,而且积累到研究数学问题的具体经验,落实学生数学素养的发展。

