理解图形特征 发展思辨能力
——《轴对称图形》教学实录
文|章 剑
【教学内容】
浙教版教材四年级下册第64、65页。
【教学过程】
一、初步感知,判断轴对称图形
●教学片断——认识对称轴和轴对称图形。师:你认识这些图形吗?
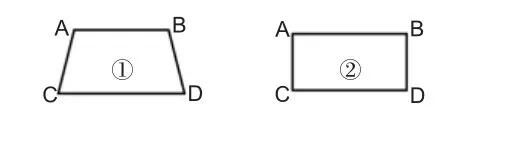

师:这些图形中哪些是轴对称图形?怎样证明呢?
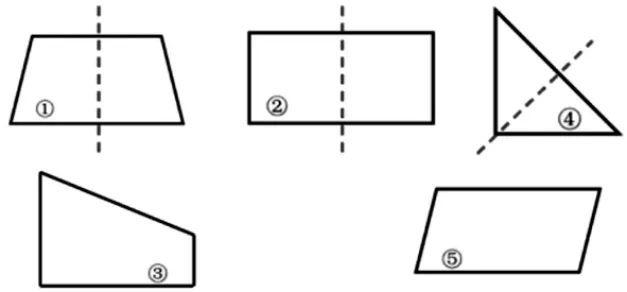
生:我觉得①②④都是轴对称图形。
生:我觉得⑤也是轴对称图形。
生:我们可以折一折,看看两边能不能重合。
师:那行,我们就按照这位同学说的,自己来验证一下。
(学生动手操作)
生:我发现①②④确实是轴对称图形。
生:我特地折了一下⑤号,发现对折后两边不能完全重合。
小结:对折以后可以完全重合,是轴对称图形;对折以后不能完全重合就不是。
追问:什么叫完全重合?①②④号完全重合了吗?
师:把这条折痕描一描——
师:①②④是轴对称图形,对折以后完全重合,这条折痕所在的直线叫作它的对称轴,我们一般用虚线来画对称轴。
【设计意图:直接从学习过的基本图形入手,创设视觉简洁、可聚焦分析的问题情境,迅速反映学生已有的认知水平。通过交流和总结,明确知识点,使绝大多数学生起点一致,都有可能参与接下来的学习。】
二、研究图形,辨别三种材料
●教学片断——用对称点研究轴对称图形。
1.明确问题。
(1)任务驱动:不对折,你能验证它是轴对称图形吗?如何验证?
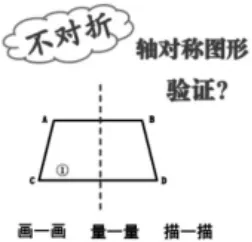
(2)提供两份学习材料。
材料一:空白纸上的图形和三角尺。

材料二:方格纸上的图形。

师:想一想,你选择哪一个学习材料进行研究?还有困难的,老师这里还有材料三。
材料三:有对称点的方格纸上的图形。
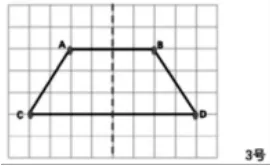
(学生独立研究,集体交流)
2.独立研究。
3.集体交流。
(1)材料比较。
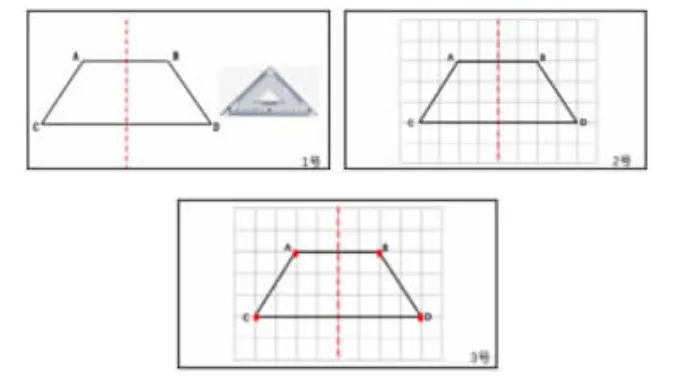
师:你觉得材料发生了什么变化?
生:我发现有些是有方格的,有些没有。
生:我还发现材料三是有点的。
生:那这些点有什么用呢?
生:是不是可以从对称点的角度进行研究。
师:说到对称点,老师这里收集到这样的一幅作品,看看你能读懂吗?

生:数一数点到对称轴有几格。
追问:有什么发现吗?
生:点A和点B到对称轴的格子数是一样的,点C和点D也是。
(2)认识对称点。
师:为什么拿点A和点B比,点C和点D比?
生:因为想象一下,对折过去,点A很有可能是和点B重合的。
生:是啊!而且这样对折过来,点C也很有可能是和点D重合。
小结:在数学上我们把这样一对到对称轴距离相等的点叫作对称点,对称点的方向是相反的。我们可以这样说:A与B互为对称点,C与D互为对称点。
(3)审读材料。
师:老师还收集到这样的一些想法,你有什么问题要问他们的?

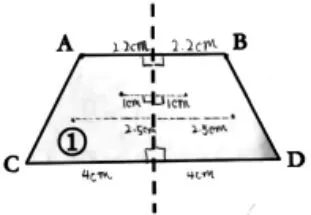
生:第一幅图为什么要量两条斜边的长度?
生:因为对折过来,A点和B点,C点和D点会重合,那么它们的长度就要一样。
追问:如果D点向右移动,它还是一个梯形。这时候它还是轴对称图形吗?
生:那就不是了,因为右边就比左边大,不能完全重合。
生:也可以说C点到对称轴的距离远,而D点近,对称点到对称轴的距离不一样。
生:所以我觉得不是所有的梯形都是轴对称图形,只有等腰梯形才是轴对称图形。
生:第三幅图我没有看懂,是什么意思?
生:我是想两边的面积是一样的,这样对折后才能完全重合。
追问:面积相等就可以了吗?
生:形状也要相同。
生:就是说边、角都要对称。
生:点、线、角、面都是对称的关系。方向相反,大小相等。
【设计意图:思辨“所有的梯形都是轴对称图形吗?”促进学生的交流,使对称概念从直观、笼统走向可描述、可分析,锻炼和提升学生的推理和论证能力。】
三、深入思辨,寻找对称点
●教学片断——感受轴对称图形有无数组对称点。
1.方格图上找对称点。
猜想:你能找到几组对称点?
探究:找第三组对称点,说说你是怎么找的?
生:我在AC的中间找一点,在BD的中间找一点,这两点就是对称点。
追问:你是怎么想的?
生:这两点到对称轴的距离都相等。
小结:对称点有无数组,每一组到对称轴的距离都相等。任意一点都能在图形的另一半找到对应的点。
2.空白纸上找对称点。

师:现在方格背景没有了。如果在梯形里面点上一点,你能在图形的另一半找到这个点的对应点吗?可以怎么找?
生:从这个点出发画对称轴的垂线段,量一量是多少厘米,在图形的另一半也画这么长的垂线段,这一点就是要找的对应点。

生:两个点到对称轴的距离是相等。
学生反馈交流。
师:你知道这位同学是怎么找的吗?好在哪里?
生:有距离,有垂直符号。
对比:这么多组对称点都找对了吗?它们有什么共同之处?
生:每组对称点到对称轴的距离都相等。
师:想象一下,对称点有无数组,它们的连线就会有无数条,这无数条连线密密麻麻铺在一起就成了面。
【设计意图:从静态分析到动态想象,借助连续画出对称点的静态画像,引导学生想象点动成线,线动成面,发展空间观念。】
四、明辨内化,正反例研究
1.反思。
任务一:验证②号和④号是轴对称图形。
任务二:验证③号和⑤号不是轴对称图形。
2.自主思考,同桌交流。
师:任务一你是怎样来验证的?
生:任意画一个点,都能在图形的另一半找到和它对称的点,能找到无数组对称点。
师:哪些同学选择的是任务二?你是怎样来验证的?
生:我是假设这一条是对称轴,我发现点A找不到对称点。
生:我有一个疑问,我发现在轴对称图形上能找到无数组对称点,在平行四边形上也可以。一直找都能找到对称点,为什么它不是轴对称图形?
生:这个点在图形的另一半就找不到对应点。找到了很多组也不一定,只要有一个点在图形的另一半找不到对应点,它就不是轴对称图形。
小结:看来,对称点不但能帮助我们验证是轴对称图形,还能验证不是轴对称图形。
【设计意图:从正例到反例的思辨。“在平行四边形上也能找到很多组对称点,为什么它不是轴对称图形?你能说服老师和同学吗?”这个问题引导学生去反思自己对轴对称图形的认识是否出现了偏差?轴对称图形是图形上的任意一点都能在图形的另一半找到对应的点——这里不仅仅是多,最重要的是任意。因此,只要找到一个点不符合要求它就不是轴对称图形,学生在这个过程中充分体会到“反例”的意思,更加深了对归纳法的理解,又是一次思维的提升。】

