基于贝叶斯推断的时变流场下污染源反演

朱建杰，周晅毅，顾 明

（同济大学土木工程防灾国家重点实验室，上海 200092）

当公共场所发生毒气袭击或者化工厂发生危化品泄漏时，需要快速对泄漏源进行定位和强度评估，从而给疏散民众和制定应急措施提供指导。由于事故发生时，流场和浓度场往往具有随时间变化的特性，因此在时变流场下进行污染源参数反演具有重要的应用价值。

污染源参数反演的主要方法有直接求解法［1-2］、优化方法［3-4］和概率方法［5-6］。直接求解法通过构造控制方程的反问题，直接求解源参数。Zhang等［1］利用Tikhonov 正则化法［7］反演了污染源强度，得到了污染物释放速率的变化曲线。Wei 等［2］将Tikhonov正则化法和贝叶斯方法相结合，得到了多个污染源的污染物释放速率和污染源位置的概率分布。优化方法通过构造目标函数，求解使目标函数最小的源参数。江思珉等［3］利用模拟退火算法反演了地下水污染源的源强度。曾令杰和高军［4］通过遗传算法对空调系统引发的污染进行了快速溯源。贝叶斯概率方法考虑了测量浓度和模拟浓度之间的误差，将误差量化为似然概率，通过贝叶斯公式计算相应源参数的概率分布。Keats 等［5］利用伴随方程求解传感器的伴随浓度场，使模拟浓度的计算量大大降低，得到了非时变浓度场下污染源位置和强度的概率分布。Guo 等［6］考虑了污染物浓度场从零浓度状态到稳定状态的变化过程，利用MCMC（Markov chain Monte Carlo）抽样算法直接对符合后验概率的样本参数进行抽样，获得了污染源的位置和强度信息，然而该研究的污染源所在的流场仍然是不随时间变化的。

本文在Keats［5］、Guo［6］的研究基础上，将基于贝叶斯推断的污染源参数反演方法扩展至时变流场的场景。考虑了流场变化对浓度场的影响，求解伴随方程得到了不同污染源参数下传感器位置处的模拟浓度，再通过贝叶斯公式计算相应污染源参数的后验概率。比较了不同位置污染源的参数反演效果，还讨论了利用污染物扩散不同阶段的测量浓度数据时，不同测量数据对反演效果的影响。

1 贝叶斯推断

1.1 贝叶斯公式

贝叶斯公式可表示为

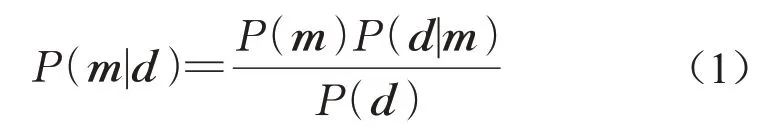
式中：P（m|d）为后验概率，是已知测量浓度为d条件下，污染源参数的概率分布；P（m）为先验概率，是未知测量信息情况下的污染源参数概率分布；P（d|m）为似然概率，表示在污染源参数为m的条件下，模拟浓度c与测量浓度d之间的相似程度。测量浓度d为传感器测量得到的浓度，模拟浓度c通过污染物扩散数值模拟获得。

对于本文的污染源参数反演问题，污染源参数为m=｛xs，ys，zs，qs｝，其中xs，ys，zs为污染源的空间坐标，qs为污染物的释放速率；测量浓度d=｛d1，1，d1，2，…，di，j，…，dN，M｝，其中di，j表示第i个传感器第j个测量浓度值，M为每个传感器记录数据的总数，N为传感器的数量。

1.2 先验概率

先验概率是在未得到任何测量信息情况下污染源参数的概率。这里认为先验概率服从均匀分布，即：

式中：C为常数。

1.3 似然概率

似然概率表示污染源参数为m的情况下，模拟浓度c与测量浓度d之间的相似程度，通常用它们之间误差的概率来表达。许多学者［5-6，8-13］认为模拟浓度c与测量浓度d之间的误差符合高斯分布，也有一部分学者［14-16］考虑到不同传感器之间的浓度值存在量级差，认为利用对数高斯分布描述误差可以降低量级差对反演准确性的影响。考虑到高斯分布在污染源反演研究领域应用更加广泛，并且具有良好的反演效果，故本文采用高斯分布描述模拟浓度与测量浓度之间的误差，似然概率为

式中：ci，j（m）表示污染源参数为m的情况下第i个传感器第j个模拟浓度值；σi，j为模拟浓度ci，j（m）和测量浓度di，j之间误差的标准差。假设误差与测量浓度处于同一量级［11-13］，可以将误差标准差σi，j设为与测量浓度di，j相同的值，即：

由于反演需要利用不同时刻多个传感器的浓度信息，假设不同测量值之间相互独立，可以将所有测量浓度对应的似然概率相乘。于是，式（1）中的似然概率P（d|m）表示为

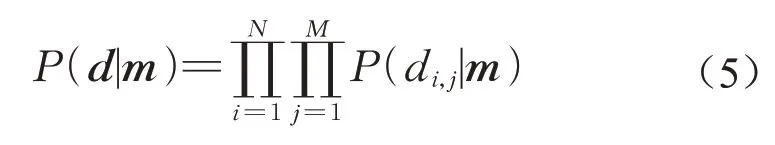
2 模拟浓度计算方法

利用贝叶斯推断解决污染源参数反演问题，往往要计算特定源参数条件下的模拟浓度ci，j，传统的模拟浓度计算方法需要解对流扩散方程。为了获得完整的污染源参数后验概率分布，须求解所有可能污染源参数条件下的对流扩散方程。这种方法的计算量十分庞大，反演的效率非常低。Keats 等［5］提出利用伴随方程计算模拟浓度，使得模拟浓度计算问题变得高效且结果精确。下面将对时变流场中的伴随方程进行推导。

2.1 对流扩散方程

对流扩散方程为

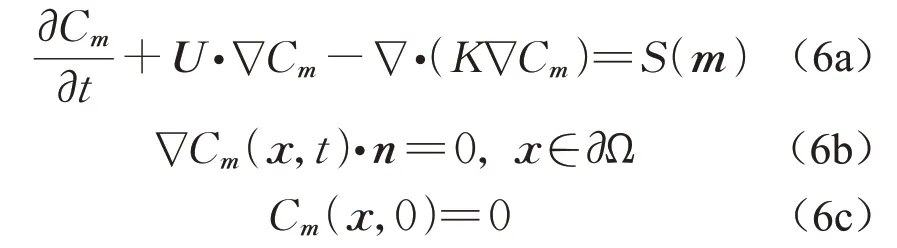
式中：Cm为源参数为m条件下的模拟浓度场；U为污染源所在的流场；K为扩散系数；S（m）为源项。当污染物释放速率恒定且污染源为点源时，S（m）=qsh（x-xs，y-ys，z-zs），其中h（·）为delta函数，表示仅在坐标为xs，ys，zs的位置存在释放速率为qs的污染源。式（6b）和式（6c）分别为对流扩散方程的边界条件和初始条件。模拟浓度场Cm与传感器模拟浓度ci，j（m）的关系为

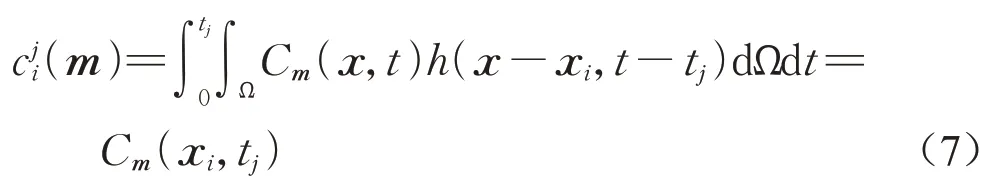
式中：xi=｛xi，yi，zi｝表示第i个传感器的空间坐标；tj表示第j个测量数据的测量时刻。

由于污染物扩散对流场的影响较小，故对流扩散方程（6a）的流场U不会受到源项变化的影响。在这种情况下，浓度场Cm与污染物释放速率qs呈线性关系；而浓度场Cm与污染源位置xs，ys，zs呈非线性关系。当污染源位置发生变化时，需要求解新的对流扩散方程，再通过式（7）计算传感器位置处的模拟浓度。对流扩散方程的求解是非常耗时的，由于在一次反演中污染源往往存在非常多的潜在位置，若对每一个潜在位置都求解对流扩散方程，反演计算的效率将变得非常低。

2.2 伴随浓度

为了快速计算任意参数条件下传感器位置处的模拟浓度，引入了伴随浓度C*这一变量。将伴随浓度C*与源项S（m）相乘，将其乘积在时间和空间上积分得到：

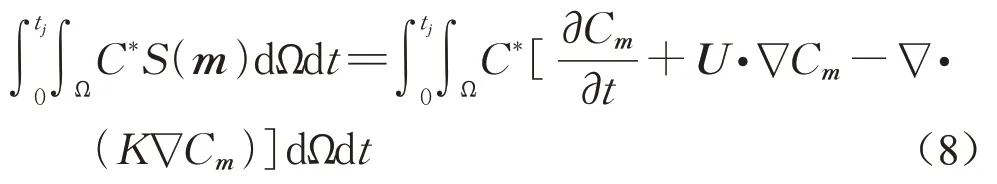
利用分部积分法和高斯公式，可以将式（8）转化为

伴随方程（10a）可以理解成以传感器为源项，在tj时刻存在脉冲的污染物释放，同时将时间推进方向和流场速度方向进行反向处理后得到的对流扩散方程。当对流扩散方程（6a）满足边界条件（6b）和初始条件（6c）并且伴随方程（10a）满足边界条件（10b）和初始条件（10c）时，式（9）中ndSdt=0，可得到伴随浓度场C*与传感器模拟浓度ci，j（m）的关系式：

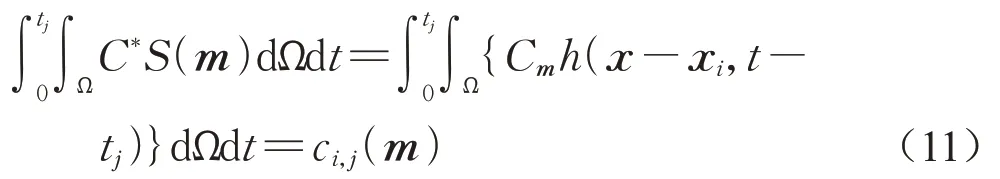
以上为利用伴随方程计算模拟浓度的推导过程。由伴随方程（10a）可知，伴随浓度场C*i，j跟源参数m无关，它仅跟第i个传感器的坐标和测量时刻tj相关。当传感器位置xi和测量时刻tj不变时，计算不同源参数条件下的模拟浓度只需将相应源项S（m）代入式（11）即可，式（11）只涉及积分运算，而利用对流扩散方程时需要求解偏微分方程，前者的计算量远远小于后者，这样就可以极大地加快反演效率。设每个传感器测量的次数为M，传感器的数量为N，则所需求解伴随方程的总数为M×N。

3 算例分析

3.1 污染物扩散数值模拟

3.1.1 模拟工况

如图1 所示，建筑模型尺寸为0.1 m×0.1 m×0.2 m（L·B·H），其周围存在A、B、C、D、E 5 个不同位置的污染源，均位于地面，用空心方块表示，对5个污染源分别做污染物扩散数值模拟。来流剖面遵循指数律，建筑顶部高度处风速为uH=4.2 m·s-1，指数α=0.25。10个传感器位于建筑背风侧，用实心黑点表示，编号为1～10，位于距地面0.062 5H高度处。

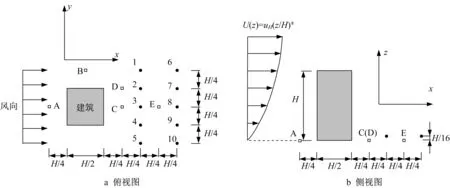
图1 污染源与传感器布置方式Fig.1 Layout of sources and sensors

3.1.2 计算域与模拟设置

根据日本建筑学会的计算流体动力学（computational fluid dynamics，CFD）指南［17］，计算域（图2）尺寸设为3.4 m×2.0 m×0.8 m（17H·10H·4H）；计算域入口与建筑模型的距离为4.5H；计算域的侧面和出口与建筑模型的距离分别为4.75H和12H。

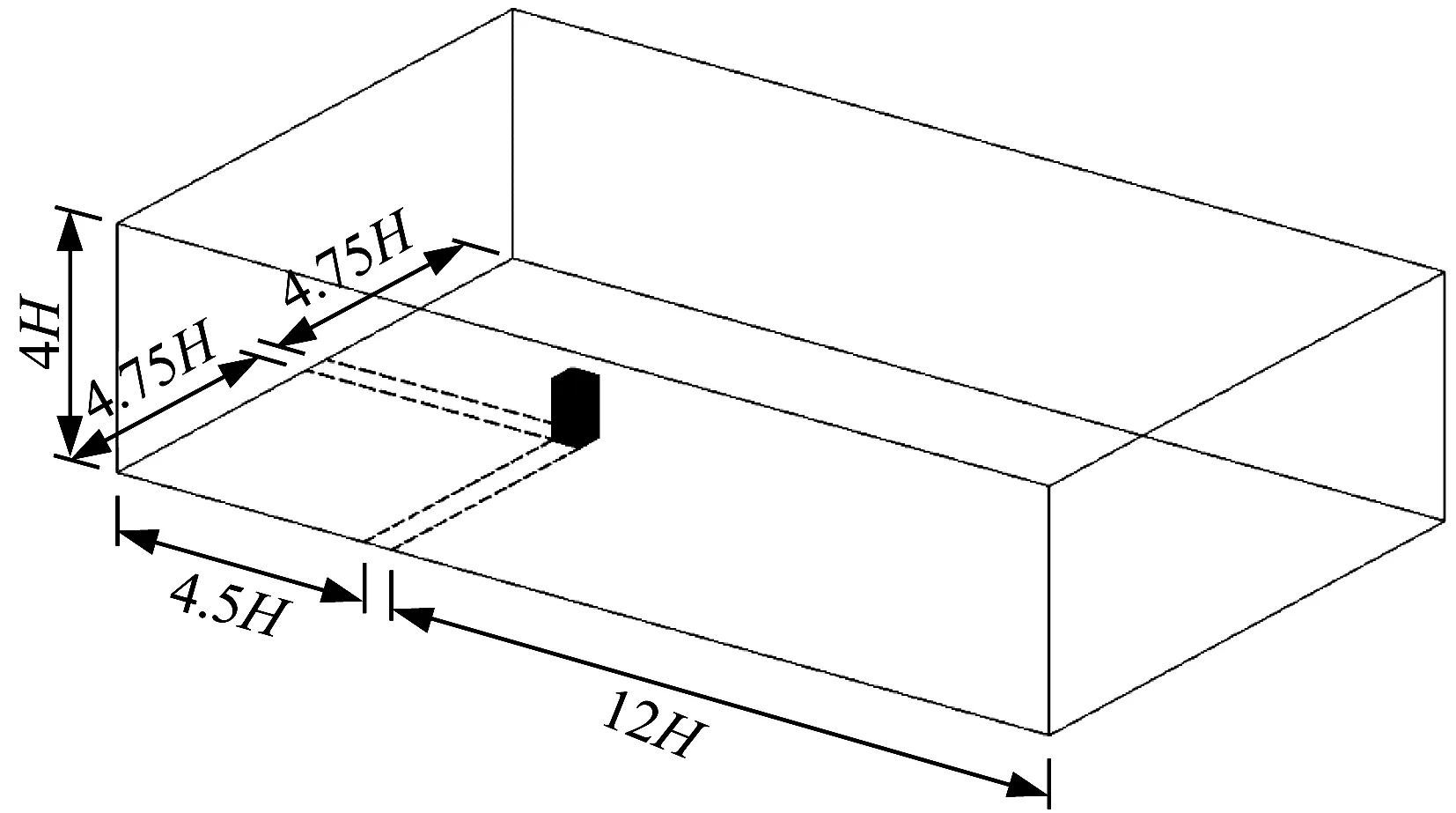
图2 计算域Fig.2 Computational domain

流场模拟以及污染物扩散模拟参数设置如表1所示，湍流模型采用剪切应力输运（shear stress transfer，SST）k-ω；流场的计算时间为50 s（1 050H/uH）。当流场已经达到稳定（t=630H/uH）时，污染物开始释放。由于该模拟工况与日本东京工艺大学于2006年做的污染物扩散风洞试验工况类似，故来流平均速度u和湍动能k根据试验数据确定，释放速率为qs=5.83×10-6m3·s-1。

表1 边界条件与数值模拟设置Tab.1 Boundary conditions and solver settings for simulation case

3.1.3 网格无关性检验

为了确保模拟结果不受网格划分方案影响，需要进行网格无关性检验（表2）。计算域采用结构化网格划分，建筑模型周围以及传感器附近区域进行了网格加密，粗、中、细三种网格的最小单元尺寸分别为H/20、H/30和H/40，网格的伸缩比设置为1.05，总网格数分别为571 400、1 254 123和2 105 408。

表2 网格无关性检验参数设置Tab.2 Parameter settings of grid independent analysis test

图3 为污染源C 处释放的污染气体在建筑模型下风向0.5H和H位置且y=0 处的模拟浓度剖面，可见仅在建筑下风向0.5H且高度大于1.2H的位置处，粗网格条件下模拟得到的气体浓度小于中网格和细网格条件下的模拟结果，其他位置处三种网格的模拟浓度曲线重合度较高，故本文选取中网格对污染物扩散进行数值模拟。

图3 不同网格划分方案的平均浓度剖面Fig.3 Profile of mean concentration for different meshing schemes

3.1.4 自保持性验证

为了保证计算域入口至建筑模型处的来流剖面不会发生显著变化，需要进行自保持性验证。图4a为空风场条件下，数值模拟和风洞试验中的x向平均风速剖面从计算域入口至建筑位置处的变化情况。在数值模拟结果中，x向平均风速从计算域入口至建筑位置处的变化较小，与风洞试验的测量结果也较为吻合。图4b为空风场条件下，数值模拟和风洞试验中的湍动能剖面从计算域入口至建筑位置处的变化情况。数值模拟和风洞试验得到的湍动能均出现了一定的衰减，相比风洞试验结果，数值模拟的湍动能衰减程度更大。Kim和Baik［18］研究了数值模拟中湍动能对污染物浓度的影响，根据研究结果可知本文数值模拟中的湍动能衰减对污染物浓度场的影响不大。

图4 空风场条件下的x向平均风速与湍动能剖面（y/H=0）Fig.4 Profile of mean velocity in x direction and turbulent kinetic energy in empty wind field (y/H=0)

3.1.5 流场

图5 为3 号传感器位置处的x向的风速（u）时程，流场稳定后的风速存在有规律的周期性波动。

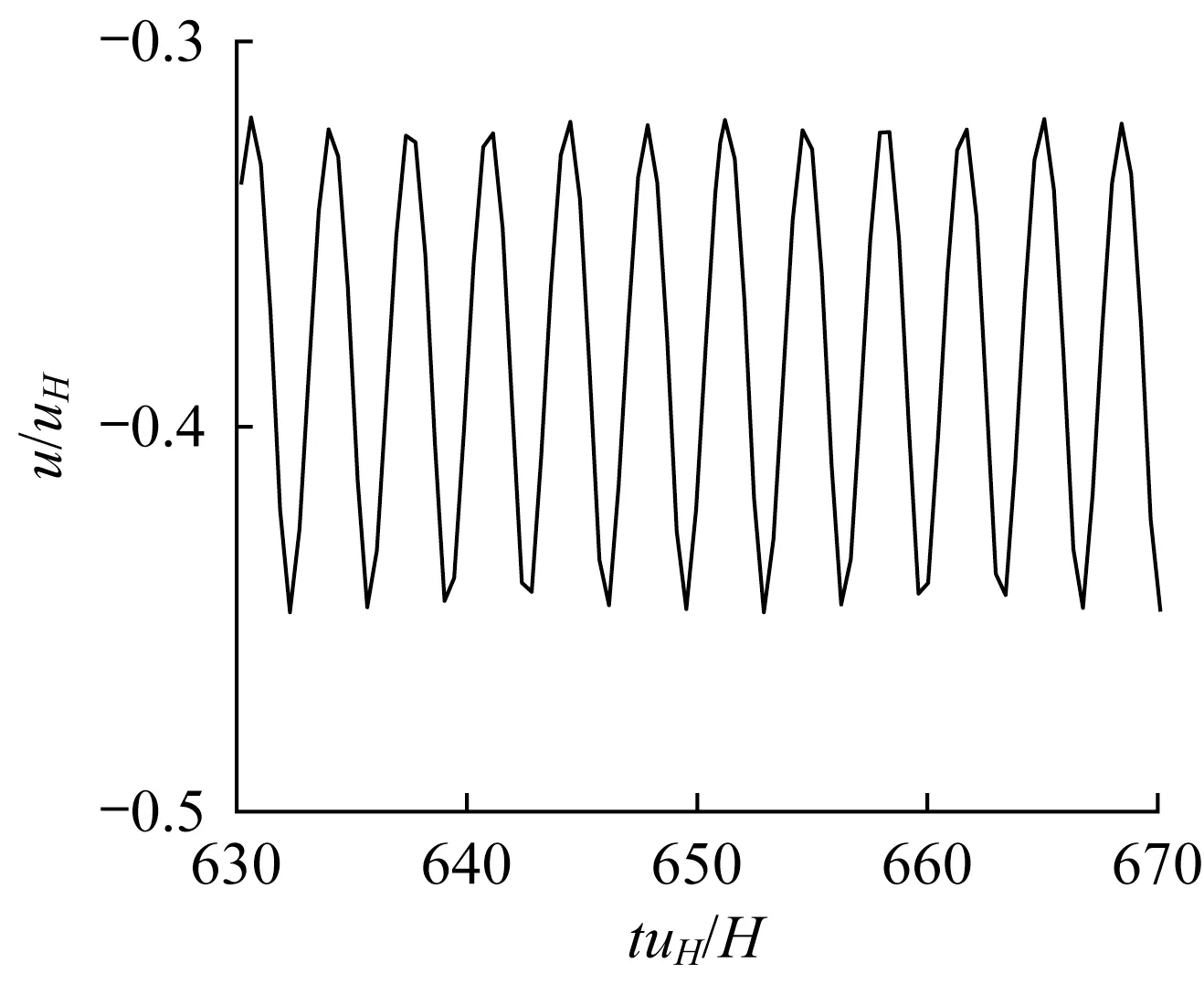
图5 3号传感器处x向瞬时风速时程Fig.5 Temporal velocity in x direction for Sensor 3

3.1.6 对流扩散方程计算测量浓度

当流场已达稳定状态（t=630H/uH）时，释放污染物气体。图6 给出了分别由污染源A～E 释放的污染气体，扩散至3 号传感器位置处随时间变化的浓度，图中的浓度值经过了量纲一处理，其中c0=qs/（uH·H2）=34.7×10-6。从污染物释放初期（t=630H/uH）开始，浓度由零逐渐发展至稳定，受到周期脉动的流场影响，污染物的浓度在发展过程中和稳定后均表现出有规律的周期波动特性。这里通过对流扩散方程（6a）对浓度场进行求解，将式（7）的计算结果作为传感器的测量浓度d。

图6 3号传感器浓度时程Fig.6 Concentration history for Sensor 3

为了在后续研究中探究利用污染物扩散不同阶段的测量数据反演源参数时不同测量数据对反演结果的影响，以t=660H/uH为分界将污染物扩散过程划分成两个阶段。在t=660H/uH之前为发展阶段，在t=660H/uH之后为稳定阶段。由于3号传感器的浓度时程最具有代表性，其他传感器的浓度变化与之类似，故不再画出其他传感器的浓度时程图。

3.1.7 伴随方程计算模拟浓度

2.2 节介绍了在计算任意源参数条件下某一传感器位置处某一时刻的模拟浓度时，基于伴随方程的计算方法在节省计算量方面具有优势，故本文通过求解伴随方程（10a），再利用式（11）计算模拟浓度。图7 对比了污染源分别为A～E 时，3 号传感器位置处的测量浓度和模拟浓度的计算结果。当污染源为A时，模拟浓度与测量浓度相比偏小；当污染源为B时，模拟浓度与测量浓度相比偏大；对于其他位置的污染源，两种浓度的计算结果基本保持一致。虽然污染源分别为A 和B 时，测量浓度和模拟浓度在3 号传感器位置的结算结果存在差异，但是两者均表现出了一致的周期性波动趋势，数值上的误差可能是由网格划分、微分方程离散和四舍五入等因素导致的，这表明基于伴随方程的模拟浓度方法可以在忽略数值误差的情况下达到与基于对流扩散方程时相同的效果。在反演的过程中，这里的误差可以作为数值模拟与实际测量的差异。值得注意的是，在基于对流扩散方程计算5 个不同位置污染源产生的污染物扩散至3号传感器位置处在某一时刻的模拟浓度时，须求解5 种源参数条件下的对流扩散方程；而基于伴随方程的方法只需针对3 号传感器在同一测量时刻求解一次，即可达到相同效果，大大节省了计算量。

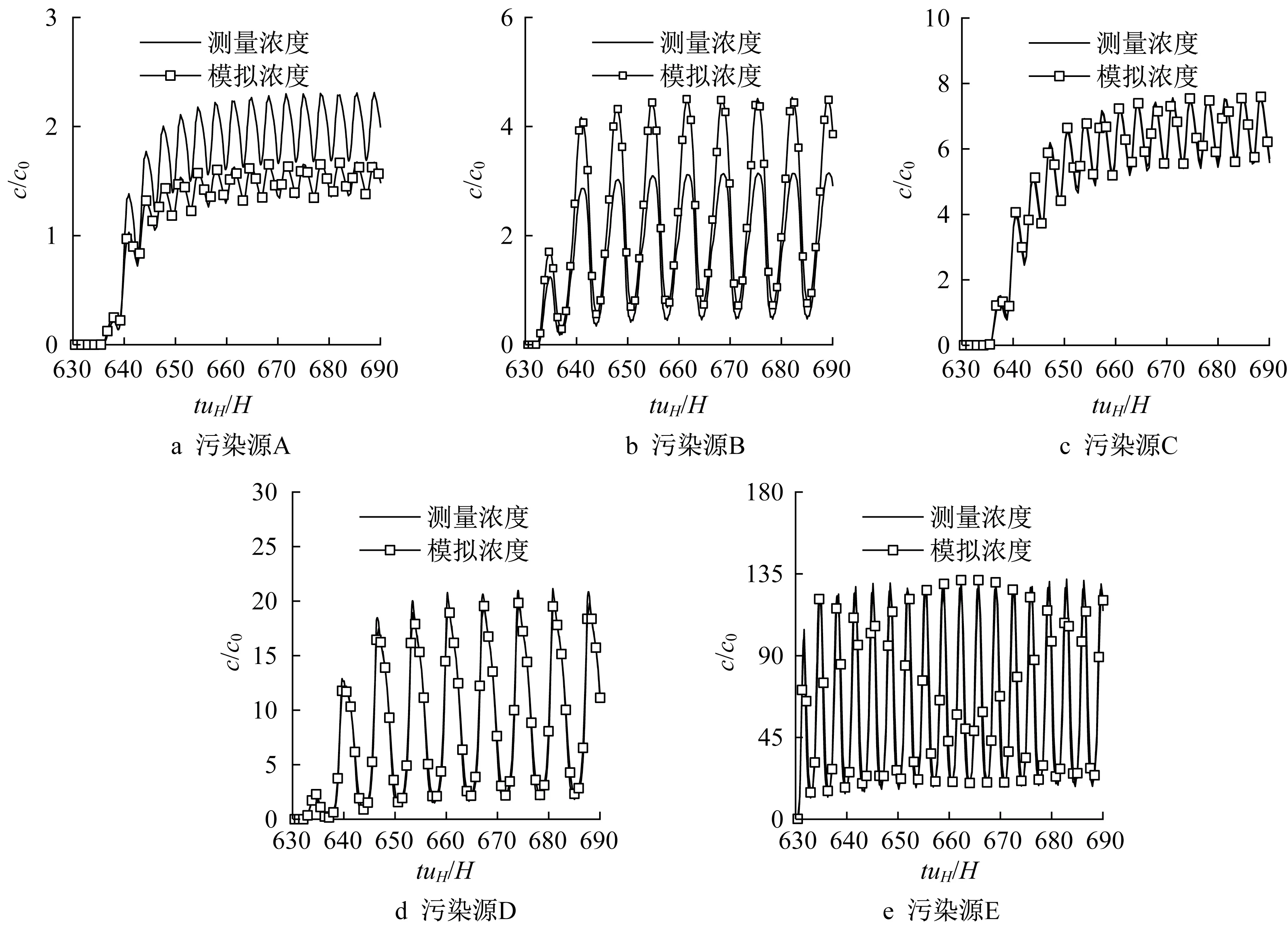
图7 3号传感器位置处测量浓度与模拟浓度比较Fig.7 Comparison of measurements and simulated concentrations at location of Sensor 3

3.2 污染源参数的后验概率

假设污染源位于地面，即污染源的竖向坐标zs=0，因此仅对污染源的xs、ys坐标和污染源的污染物释放速率qs进行反演。

3.2.1 污染源参数的传感器与污染源相对位置的影响

图8、图9 给出了当污染源分别位于A～E 时通过贝叶斯推断得到的污染源位置和强度的后验概率。在污染源位置的后验概率云图中，星号处为污染源的真实位置，空心圆为传感器；在污染源强度的后验概率柱状图中，虚线表示污染源的真实强度。污染源A位置的后验概率分布在x方向呈较宽的分布，后验概率均值为-1.29H，与真实值之间的误差为0.54H，后验概率极值点为-0.75H，与真实值一致，但其后验概率标准差高达0.40H，表明污染源位置x坐标的反演结果具有较大的不确定性；污染源A的强度后验概率均值和极值点分别为0.72qs和0.62qs，反演结果与真实值相比偏小。虽然污染源B位置的反演误差和不确定性与污染源A相比有所减少，但是在其强度反演结果中，后验概率分布较为平坦，后验概率均值为1.87qs，与真实值之间的误差高达87%，后验概率标准差为0.80qs，表明污染源B强度的预测可靠性较低。

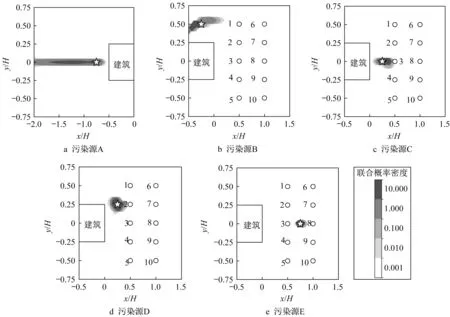
图8 污染源A～E的位置概率云图Fig.8 Probability contour of location for pollution source A-E

图9 污染源A～E的强度概率密度Fig.9 Probability density of strength for pollution source A-E

污染源A 和污染源B 的反演误差较大，是因为以A 和B 为污染源做污染物扩散数值模拟时，传感器位置处的测量浓度和模拟浓度之间存在较大的误差，所以当数值模拟不能准确反映真实的测量结果时，会导致反演出现较大的偏差。同时，在反演结果中可以发现，污染源A 和污染源B 的源参数后验概率标准差也大于其他位置的污染源。这是因为这两个污染源与传感器之间的距离较远。由似然概率式（3）可知，当污染源参数xs，、ys和qs能正确描述真实污染源时，似然概率达到最大值，即概率极值。在计算距传感器较远的污染源所产生的污染物在传感器位置的模拟浓度c（xs，ys，qs）时，模拟浓度值对于源参数的变化不敏感，即和较小，后验概率在概率极值点附近的变化不明显，导致后验概率标准差较大，因此污染源A 和污染源B 的反演结果具有较大的不确定性。为了减少反演结果的不确定性，可以根据历史信息（曾经发生过泄露的位置）和经验设计传感器布置方式。

在计算污染源C～E 产生的污染物扩散至传感器位置的浓度值时，测量浓度和模拟浓度的计算结果吻合较好，因此源参数反演的误差较小。同时，传感器的浓度值对于污染源C、污染源D 和污染源E的参数变化灵敏度较高，导致了源参数的后验概率标准差较低，反演的不确定性较小。

3.2.2 利用不同扩散阶段测量数据对反演结果的影响

如图6 所示，以t=660H/uH为分界线将污染物扩散过程分为两个阶段。第一个阶段为发展阶段，包含了污染物浓度从零浓度达到稳定状态的发展过程；第二个阶段为稳定阶段，完全由周期性波动的测量数据构成。下面分别利用污染源在C处时传感器位置处发展阶段、稳定阶段和所有时刻的测量数据对污染源参数进行反演，反演结果分别如图10、图11所示。相比利用稳定阶段的测量数据的污染源位置反演结果，利用发展阶段的测量数据可以降低位置误差和减小后验概率标准差，但稳定阶段数据提升的效果并不显著。图表中的结果也反映出利用所有时刻的测量数据时，其反演结果的精确程度提高非常有限。

图10 利用不同阶段测量数据的污染源A～E的位置概率云图Fig.10 Probability contour of location for pollution source A-E by using measurement from different stages

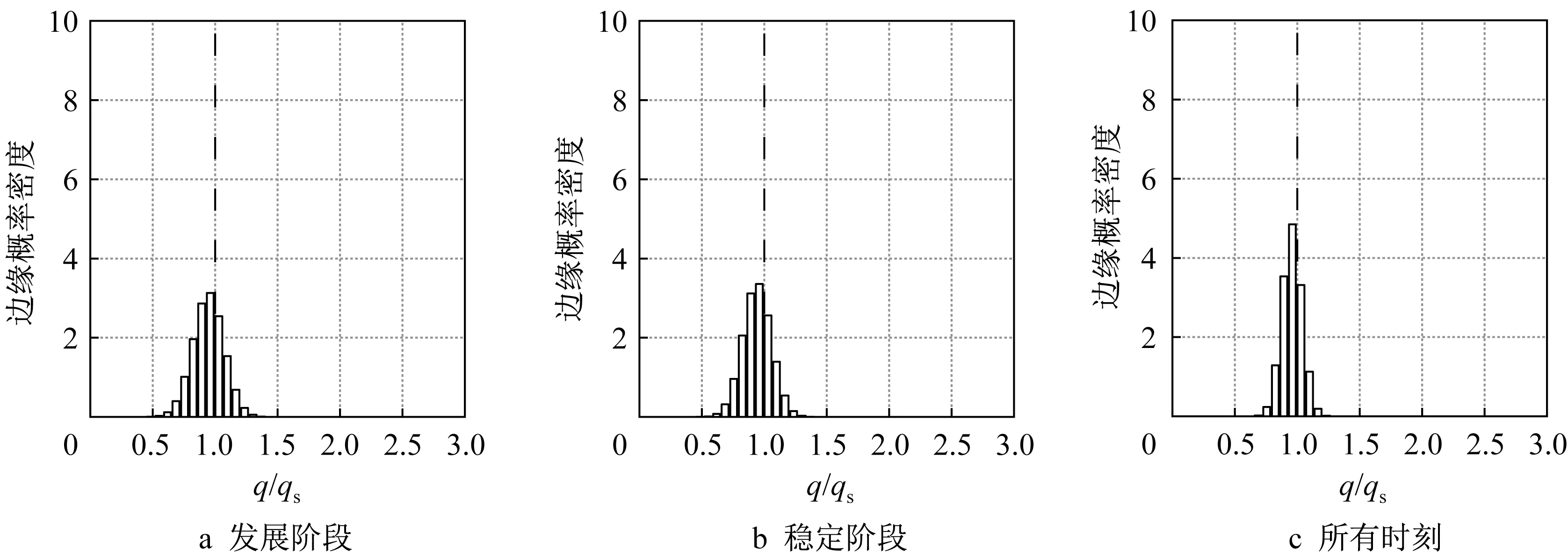
图11 利用稳定阶段测量数据的污染源A～E的强度概率密度Fig.11 Probability density of strength for pollution source A-E by using measurement from different stages

4 结论

本文基于贝叶斯推断对时变流场下的污染源参数进行了反演，比较了不同位置污染源的参数反演结果，利用不同扩散阶段的测量数据探讨了其对反演结果的影响，得到了以下结论：

（1）模拟浓度与测量浓度之间的误差是影响反演精确性的主要因素，当数值模拟能准确地反映污染物扩散时，污染源反演的准确性能够得到极大的提高。

（2）当污染源与传感器距离较近时，污染源参数的后验概率分布比较集中，反演结果的不确定性较小，真实的污染源参数可能出现在较窄的区间，污染源所需搜索的范围较小；当污染源与传感器距离较远时，污染源参数的后验概率分布较宽，反演结果的不确定性较大，真实的污染源参数可能出现在较宽的区间，需要较大范围搜索污染源。

（3）不同阶段的污染物扩散测量数据对反演结果不会造成显著的影响。

本研究的不足之处在于污染源参数反演是在已知流场的前提下进行的，流场的未知性会影响模拟浓度的计算，从而可能造成反演不准确。如何减少流场未知性对反演的影响，需要进一步深入研究。