考虑羽流浮力影响的高层建筑周围污染物扩散数值模拟
周晅毅,马慧心,顾 明
(同济大学土木工程防灾国家重点实验室,上海 200092)
近年来,随着城市化和工业化进程的不断推进,环境污染问题引起了公众的广泛关注。建筑周围气体污染物的释放与扩散给城市环境质量及居民生命健康带来了极大危害。对气体污染物的扩散进行正确模拟,包括对时均浓度以及瞬时浓度的预测,可以为制定相应的应急管理措施提供重要参考信息。
由于羽流的运动会受到风和建筑结构之间复杂相互作用的影响,建筑周围污染物的扩散过程将会受到其自身的物理特性、大气边界层稳定性、周边建筑形态等因素的影响。在建筑后方尾流区等弱风区域,由环境空气与污染物之间的密度差异所产生的羽流浮力效应是驱动污染物扩散的重要因素。轻质污染物由污染源处释放后,由于其密度小于周围空气,所受到向上的浮力大于自身重力,从而产生了向上的合力,这里称之为正浮力;而重质污染物密度大于空气,向上的浮力小于自身重力,产生了向下的合力,这里称之为负浮力;正负浮力均会对污染物的浓度分布产生重要影响。因此,研究密度差异所引起的浮力效应影响对污染气体输运的预测具有重要意义。
目前,建筑周围污染物扩散的主要研究方法有以下三种:现场实测、风洞试验和数值模拟[1]。现场实测可以提供实际情况下气体扩散的第一手资料,但受气象条件等因素的影响,现场实测的结果通常难以得到重现。风洞试验具有试验边界条件可控的优势,但对于考虑浮力效应的湍流扩散过程,其在满足密度弗劳德数的相似准则时需要较低的风速,这给满足雷诺数独立性的假定带来了一定的困难[2]。基于计算流体动力学理论的数值模拟是研究污染物扩散问题的另一有力工具,目前已被广泛采用[3]。相对于现场实测和风洞试验,数值模拟方法成本较低且研究周期短[4];同时,可以克服风洞试验受相似准则限制的弊端,并能够提供细致的流场及浓度场数据,在现象分析及机理研究方面具有优越性。常用的数值模拟方法主要包括雷诺平均方法(Reynolds-averaged Navier-Stokes simulation,RANS)和大涡模拟(large-eddy simulation,LES)。Olvera等[5]采用定常RANS方法对从立方体建筑后方释放的中质及轻质羽流的扩散进行了数值模拟,发现正浮力会在尾流区引起较大的流动扰动,从而使建筑背风面的浓度较高,而建筑下游地面处的浓度较低。相对于单独讨论正负羽流浮力的作用,在相同几何条件及模型设置下将二者同时考虑更有利于对比分析其对流场及浓度场的影响机理,进一步总结出相应的规律。目前,同时考虑正负羽流浮力影响的研究仅有Tominaga和Stathopoulos[6]针对立方体建筑周围的扩散问题所进行的模拟,该研究采用RANS方法进行,指出RANS方法的数值特性限制了建筑后方湍流及气体污染物浓度分布的预测精度,但缺少对不同羽流浮力影响下浓度输运通量及浓度瞬态变化特性的分析。
随着计算资源的不断进步,近年来大涡模拟方法得到了广泛关注[7]。LES方法直接求解大尺度漩涡,仅需要对各向同性的小尺度漩涡采用模型进行处理。相较于RANS方法而言,前人研究[8-10]发现在羽流浮力可以忽略的情况下LES方法对污染气体扩散的预测精度更高。除此之外,LES 方法还可以提供羽流扩散的重要瞬态信息。但是,目前采用LES方法讨论羽流浮力影响的文章相对较少。Wingstedt 等[11]对中质和重质气体的扩散进行了大涡模拟,发现与中质气体相比重质气体的羽流外形会更宽更浅,且受下游立方体阵列高度的影响更大。Lin 等[12]以单一立方体建筑为研究对象,比较了RANS和LES方法对受正浮力影响的气体浓度分布的预测精度。
如前所述,前人对于浮力效应影响下污染物扩散的研究大多以立方体建筑为研究对象且侧重于数值方法的对比验证,目前很少有针对高层建筑周围浮力气体扩散的分析;同时,关于浮力对时均及脉动浓度场、污染物标量输运机制影响的讨论并不充分。因此,本文同时考虑正负浮力的影响,采用LES方法模拟了一个高层建筑周围的流场及浓度场分布,总结了不同羽流浮力影响下高层建筑周围污染物时均浓度场的分布特征,并对羽流浮力对浓度输运机制、浓度脉动的影响进行了探讨。
1 模拟案例概要
本文中的研究对象根据东京工艺大学的风洞试验模型[13]布置,如图1所示。

图1 结构布置示意图Fig.1 Schematic diagram of the building model
高层建筑模型置于中性大气边界层中,建筑模型沿x、y、z坐标方向的尺寸分别为0.08 m(B)×0.08 m(B)×0.16 m(H)。污染源直径ϕ为5 mm,其圆心距离建筑背风面的距离为0.25H。来流垂直于建筑的迎风面。为了研究正负羽流浮力对高层建筑周围气体污染物扩散的影响,设置了如表1所示的工况。这里,量纲一参数密度弗劳德数(Fr)按照公式(1)定义,用以表征污染物所受到的浮力与环境空气的惯性力之间的相对大小;ρs和ρa分别为污染物密度和空气密度,Δρ=ρs-ρa为污染物与空气之间的密度差值,g为重力加速度。各工况的入口风剖面和湍动能剖面由试验数据(EXP)拟合得到,如图2中的实线所示。其中,工况1 在建筑高度处的顺流向平均风速UH=1.40 m·s-1,与风洞试验保持一致,用以验证数值模拟的准确性。工况2~工况4中UH均为0.60 m·s-1,根据环境空气与污染物之间的密度差异,有三个不同的密度弗劳德数,用以讨论气体污染物羽流浮力的影响。污染源处的气体总释放率为q=2.62×10-4UHH2,m3·s-1,对于工况1和工况2~工况4,污染源处所释放的污染物体积分数F分别为5%和100%。

表1 数值模拟工况Tab.1 Cases of numerical simulation


图2 数值模拟入口剖面Fig.2 Inflow profiles of numerical simulation
在本文中,风洞试验及数值模拟的风速均采用参考风速UH进行量纲一处理;体积浓度c用来表征污染物的浓度分布,其与污染物质量分数φ之间的关系如公式(2)所示

体积浓度数据均采用参考浓度C0进行量纲一处理,C0按照公式(3)定义:

式中:Qe=qF为污染源处污染物的体积流率。
2 数值方法与计算设置
本文采用LES方法对不同羽流浮力影响下的气体扩散问题进行数值模拟,使用商业软件ANSYS Fluent进行模拟。
2.1 大涡模拟方法
LES方法采用滤波函数对大尺度涡和小尺度涡进行区分,大尺度涡属于可解尺度,直接进行求解;小尺度涡则需要采用模型处理。滤波后的质量、动量守恒和组分输运方程如式(4)—(6)所示:

式中:“·~”表征可解尺度变量;ui为速度分量;xi为空间坐标;t为时间;ρ为流场中气体污染物和空气所形成混合物的密度;μ为流体动力粘度;p为压力;g为重力加速度;δi3为Kronecker delta 函数;φ为污染物的质量分数;D为分子扩散系数。
亚格子尺度雷诺应力τSGSij和亚格子尺度质量通量JSGSi按照公式(7)—(8)求解:
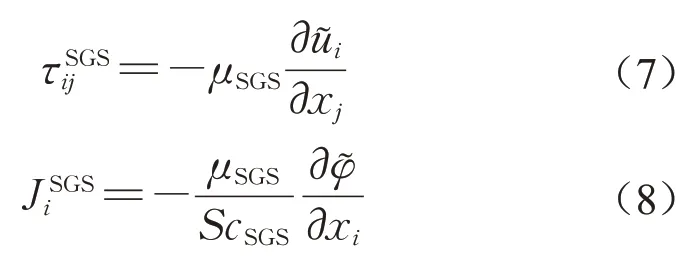
式中:μSGS为亚格子湍流粘性,需要通过亚格子模型处理;ScSGS为亚格子湍流施密特数,在本文中设置为0.7。
本文所采用的亚格子湍流模型为动态Smagorinsky-Lilly 模型,文献[14-16]已经证明该模型是建筑环境周围流动及污染物扩散模拟的合适选择。各工况的计算时间步长如表1 所示,均满足库朗数(Courant-Friedrichs-Lewy numbers)小于1.0 的要求。各工况的量纲一采样时间(t*=t·UH/H)均为840,经验证明该采样时间足以获得统计意义上收敛的变量时均值。
2.2 计算域及边界条件设置
数值模拟的计算域如图3a所示,其大小x·y·z为12.5H×7.5H×6.25H,计算域的坐标原点设置在建筑底面中心处。入口边界设置为速度入口(Velocity inlet),平均风剖面及湍动能剖面如图2 中的拟合曲线所示,湍流耗散率根据日本建筑学会(AIJ)行人风环境数值模拟指南[17]中的规定确定。入口处的速度脉动采用涡方法(Vortex method)[18]生成,涡的数目取为190[16]。出口边界条件为自由出流(Outflow),地面及建筑表面设置为无滑移壁面边界(No-slip wall),采用Kader[19]提出的混合函数进行近壁面处理;顶面及侧面设置为对称边界(symmetry);污染源设置为速度出口(Velocity inlet)。速度与压力耦合采用SIMPLEC 算法,动量及组分输运方程的离散采用有界中心差分格式(bounded central differencing scheme),压力项的离散采用二阶格式(second order),时间离散采用有界二阶隐式格式(bounded second order implicit)。

图3 计算域及网格示意图Fig.3 Schematic diagram of computational domain and grid.
3 数值方法验证
为了验证所采用的数值方法对高层建筑周围风场及污染物浓度场模拟的准确性,图4将工况1中心平面(y/H=0)上建筑后方的时均顺流向风速及时均浓度的模拟值与日本东京工艺大学的风洞试验结果[13]进行了对比。由图中可以看出,LES 方法对风场的模拟结果与实验结果呈现出较好的一致性;对于平均浓度分布,数值模拟基本重现出了建筑后方污染物的分布特征,但在建筑下方(z/H<0.5)LES的预测结果偏小。文献[20]对该试验的大涡模拟研究也得到了和本文相似的结果,在风洞试验中,靠近地面位置的浓度测量存在一定的难度及不确定性,这可能是误差产生的重要原因之一。总的来说,本文所构建的数值模型可以较好地重现高层建筑周围的流场及浓度场分布,可用于进一步讨论羽流浮力效应对污染物扩散的影响。

图4 数值方法验证Fig.4 Validation of numerical method
4 结果与讨论
4.1 平均流场
图5给出了各工况中心平面(y/H=0)处的时均垂直速度分量及流线分布。图中三角形表示污染源所在的位置,在后文的所有图片中均有相同的含义。流线图直观展示了建筑后方回流区的大小,对于本文所讨论的高层建筑,其后方回流区的长度为0.6H。整体上,羽流浮力对流场的影响较小;但在靠近建筑背风侧及污染源处,轻质气体所受到的正浮力使垂直速度分量明显增大,较大的上升气流使回流区的流线有明显的上洗现象;而重质气体工况由于向下负羽流浮力的存在,气流的爬升受到抑制,产生了相反的效果。
4.2 平均浓度场
图6为各工况在中心平面(y/H=0.1)以及z/H=0.1 平面处的时均浓度分布云图。由于污染源位于建筑后方尾流区内(x/H=0.5,y/H=0),在尾流涡的作用下,污染物自污染源处释放后朝着建筑背风墙面输运,于是在建筑背风墙面和污染源之间有较高的浓度。对于轻质气体工况,污染物羽流中心线与地面呈一个明显夹角,正浮力和尾流涡的共同作用使建筑背风侧产生了较强上洗气流(图5 a),因此污染物沿建筑背风墙面爬升并产生了较高的浓度(图6 a)。相较于无浮力及负浮力工况,在正浮力的作用下更多的污染气体突破了尾流区的限制,对建筑顶面产生了较大影响。对于重质气体工况,受向下的负羽流浮力的影响,污染物沿建筑背风墙面的爬升被明显削弱,在建筑下方(z/H<0.5)积聚形成了高浓度区域并沿着顺风向输运。同时,在z/H=0.1平面处,重质气体沿横风向的扩散较轻质气体有明显的增强。

图5 中心平面(y/H=0)处量纲一垂直速度分量(W/UH)云图及流线分布Fig.5 Distribution of time-averaged streamlines at vertical plane y/H=0 contoured by the time-averaged dimensionless vertical velocity W/UH.

图6 量纲一时均浓度(C/C0)分布云图Fig.6 Contours of dimensionless time-averaged concentration (C/C0)
为了进一步评价羽流浮力对高层建筑后方污染物浓度累积情况的影响,图7给出了三个工况在建筑后方沿顺流向若干截面的平均浓度分布情况,各个截面的尺寸均与建筑背风墙面相等。在建筑后方回流区内(0.25<x/H<0.85),受不同羽流浮力的影响,三个工况的面平均浓度差异显著。在靠近建筑背风面处,轻质气体工况的截面平均浓度最高,重质气体工况的平均浓度最低,这主要是由于在正浮力的作用下较多的污染物沿建筑背风面爬升所导致的。然而,随着截面位置沿顺流向推移,这种现象发生了反转,重质气体面平均浓度明显高于其他两种气体,尤其是在污染源所处的平面上(x/H=0.5)。在回流区下游(x/H>0.85),三工况之间的面平均浓度差异沿顺流向逐渐减小,但轻质气体始终保持最低的浓度积累水平。可见,负浮力和正浮力分别抑制和增强了建筑后方,尤其是回流区内的气体扩散。

图7 建筑后方面平均浓度(C/C0)分布Fig.7 Plane-averaged dimensionless time-averaged concentration(C/C0)behind the building
4.3 浓度输运
气体污染物浓度的标量输运受到平均流动及湍流的共同影响,二者对浓度输运所做的贡献通常用对流通量(UiC)和湍流通量()表示。浓度通量的分布反映了浓度迁移的本质,因此分析不同羽流浮力工况的对流通量和湍流通量,对进一步解释羽流浮力对污染物扩散机理的影响是至关重要的[8]。图8给出了三个工况在中心平面(y/H=0)内的量纲一对流及湍流通量分布。由图中可以看出,各个工况的对流通量和湍流通量在量级上基本一致,也就是说平均流动和湍流对污染物在竖直方向上的扩散贡献相当,这种现象也曾被Gousseau等[10]在针对不受浮力影响的污染物扩散问题研究中观察到。图8反映出,在正浮力的影响下靠近建筑背风侧的对流及湍流通量均有明显的增强,使得污染物更多的向上方输运;而负浮力则产生了相反的效应。图9定量给出了三个工况在建筑背风面后方建筑高度处的对流及湍流通量分布,在相对远离建筑背风侧的x/H>0.375位置处,三个工况的对流通量(图9 a)均出现了负值,这主要是由于尾流涡的存在(图5)而导致的。在同一位置处,三个工况的湍流通量始终为正值,即向上输运;且轻质气体工况的湍流输运强度明显大于中质及重质工况,因此,轻质气体在湍流作用下更多的从尾流区扩散出去,而重质气体则在尾流区内出现了堆积,如图6所示。

图9 建筑高度处垂直方向污染物浓度通量对比Fig.9 Comparison of vertical concentration fluxes of pollutant at the building height
4.4 浓度脉动
对于会对人们生命健康产生不利影响的有害气体,除平均浓度外,瞬时浓度也是需要关注的重点。根据Li 和Meroney[21]的定义,图10 给出了不同羽流浮力影响下建筑后方的局部浓度脉动强度ICL局部浓度脉动强度是将浓度的均方根值使用当地的平均浓度进行归一化处理,在羽流浮力的影响下,三个工况呈现出明显不同的分布特征。对于轻质工况,污染源正上方的ICL明显大于中质工况,也就是说由于正浮力的作用导致该处出现了较平均浓度而言很大的浓度脉动。重质工况的浓度脉动明显比中质工况小很多,且ICL的较大值分布在污染源顺流向的后方。值得一提的是,轻质工况的ICL峰值超过了4.0,而重质工况的ICL峰值仅在2.5左右。总的来说,轻质气体所受到的正羽流浮力使浓度脉动进一步增强,而重质气体受到的负羽流 浮力则抑制了浓度脉动。
图11 给出了各个工况在监测点位置处的脉动浓度概率密度分布(probability density distribution,PDF)图。这里共选取了三个监测点,其中A 点(0.05,0,0.128)和B点(0.05,0,0.03 2)靠近受羽流浮力影响较大的建筑背风侧分布,C 点(0.2,0,0.032)布置在尾流涡之外,各个监测点的位置如图11所示。由图中可以看出,在三个监测点位置处,不同羽流浮力影响下各个工况的脉动浓度均不服从正态分布。表2中对各个监测点处污染物浓度的统计特性进行了总结,σc为污染物瞬时浓度的均方根值,这里以污染物浓度时程数据的95%分位值作为峰值浓度(CP)。轻质气体工况在靠近建筑背风侧的A、B两点处相对于其他两个工况而言具有较高的平均浓度,同时也具有较高的峰值浓度,但浓度正值波动的出现概率相对较低。而远离建筑背风侧的C点则情况相反,在该位置处重质气体工况具有较高的平均浓度和峰值浓度,以及相对较小的浓度正值波动概率。总的来说,各个监测点处的峰值浓度可达平均浓度的2~3 倍,对于有毒有害气体的防控应该引起特别的注意。
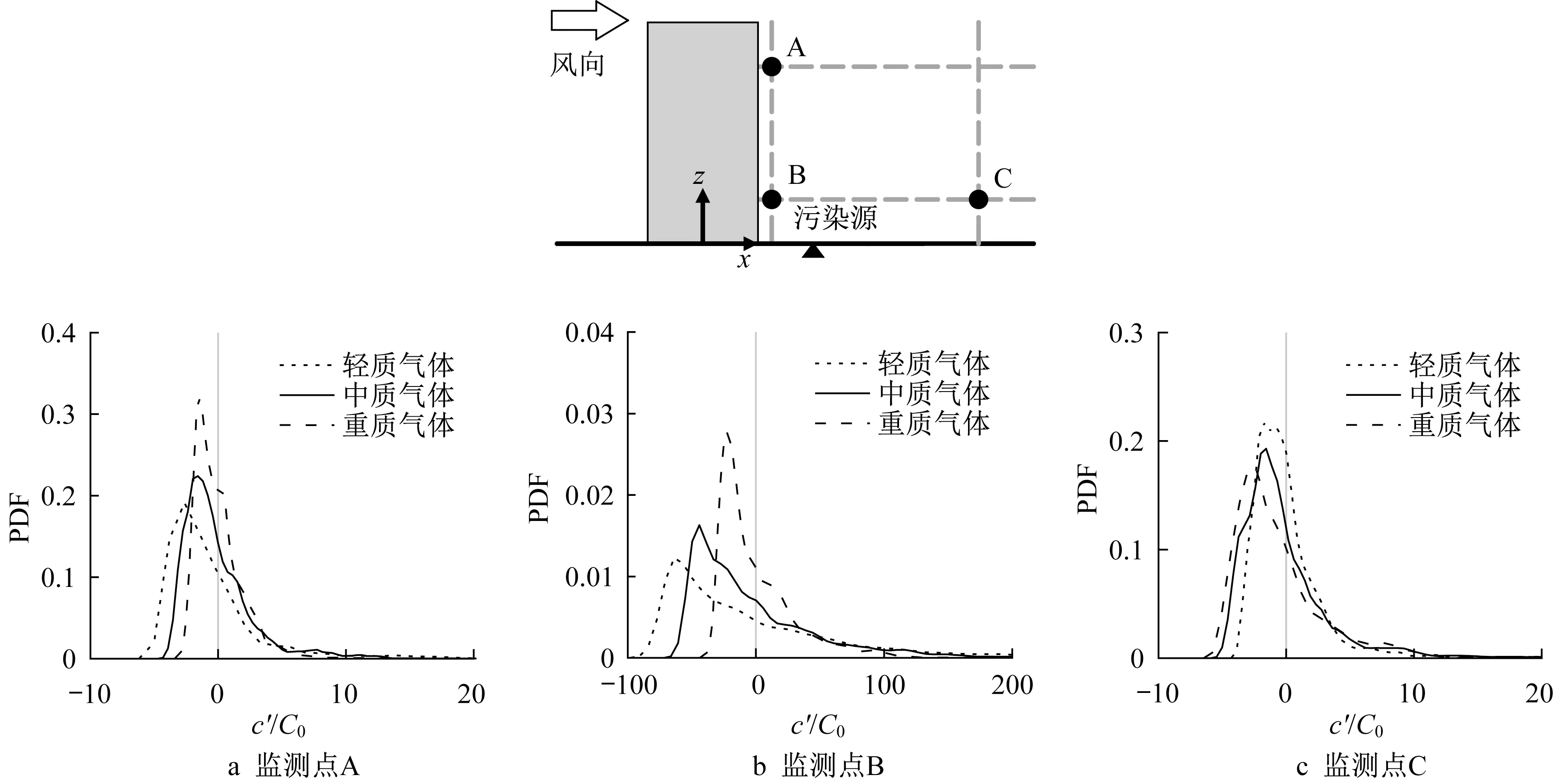
图11 监测点处脉动浓度概率密度分布图Fig.11 Probability density distribution of fluctuating concentration at three key points.

表2 污染物浓度统计特性Tab.2 Statistical characteristic of pollutant concentration.
5 结论
本文对高层建筑周围的污染物扩散问题进行了LES模拟研究,设置三个工况同时考虑了由污染物和周围空气的密度差异所产生的正负羽流浮力的影响。通过将中质气体工况下的模拟结果与风洞试验数据对比验证了数值模拟方法的准确性,并在此基础上进一步分析了不同羽流浮力对时均浓度、浓度输运以及浓度脉动的影响,得出的主要结论如下:
(1)轻质气体所受正浮力使污染物沿建筑背风面的爬升增强,从而导致靠近建筑背风侧浓度较高;而重质气体受负浮力的影响在建筑下方堆积,沿顺流向及横风向发生明显扩散。总的来说,正负浮力分别增强和抑制了建筑后方尾流区内对污染物的稀释作用。
(2)轻质气体工况靠近建筑背风侧的竖直方向对流及湍流通量相较于其他两个工况均有明显的增强,因此更多的污染物突破了尾流涡的限制,从上方扩散出去;而重质工况的对流及湍流通量均较小,导致其在尾流区内发生了堆积。
(3)轻质气体所受正浮力增强了靠近污染源及建筑背风侧的浓度脉动,而重质气体所受的负浮力则对浓度脉动有一定的抑制作用。对于不同浮力工况而言,靠近建筑背风侧及尾流区外的监测点处峰值浓度均可达到平均浓度的2~3倍。
本文仅对弗劳德数为±3.5的两个浮力气体扩散工况进行了探讨,但在实际的气体污染物扩散过程中根据羽流浮力强弱的不同可能涉及到更大的弗劳德数范围,在后续的研究工作中将设计补充工况,从而总结得出适用范围较大的一般性结论。本文针对高宽比为1:2的单体高层建筑进行了研究,而对于高宽比较小的超高层建筑、建筑群中受到环境干扰的建筑,由于受到复杂流动结构的影响,污染物的扩散特性也会有所不同,这需要在后续的工作中做进一步的讨论。除此之外,风洞试验数据的缺乏是制约数值模拟精度验证的一个问题,后续研究工作中计划针对高层建筑周围的浮力气体扩散进行风洞试验研究,获得可靠的脉动浓度数据,进一步验证数值模拟的精度。

