时间步长对格子玻尔兹曼法模拟室内气流精度的影响

韩梦涛

（华中科技大学建筑与城市规划学院，湖北 武汉 430074）

近年，基于格子玻尔兹曼法的大涡模拟（lattice Boltzmann method-based large-eddy simulation，LBM-LES）开始应用于建筑［1-3］和城市风环境［4］模拟。与当前风环境主流的有限体积法（finite volume method，FVM）在宏观尺度上求解物理量不同，LBM用虚拟的、包含有限种速度模式的微观分布函数表示流体粒子的集合，并通过分布函数的碰撞和迁移来模拟流体运动［5］。与基于FVM 的大涡模拟（FVM-LES，即风环境模拟的主流LES 方法）［6-7］相比，LBM-LES 算法简单，边界条件易于实现，且在LES 计算中无需求解压力泊松方程［8］，计算速度更快，在复杂湍流风环境模拟中具有较大潜力［9-10］。

LBM的控制方程是格子玻尔兹曼方程，其中的关键项是碰撞算子。碰撞算子的形式决定了待求解流体的性质。BGK（Bhatnagar-Gross-Krook）近似模型［11］是最常用的碰撞算子，能以简单的形式获得足够精度的模拟结果。既往研究表明，BGK算子在模拟环境风问题，尤其是室内气流中取得了较好的成果。Elhadidi等［1］利用含BGK算子的LBM模拟了较粗网格条件下室内空间的气流分布并与FVM 进行了比较。Han 等［2］则系统总结了使用LBM-LES 模拟室内空气流动时不同计算条件对模拟精度的影响，并与FVM-LES 进行了详细比较。上述研究表明含BGK算子的LBM-LES可有效模拟室内空气流动，并可取得与FVM-LES类似的模拟结果。

同时理论分析表明，利用含BGK 算子的LBMLES 可推导出低马赫数（Mach number，M）流体的连续性方程和纳维-斯托克斯（Navier-Stokes，N-S）方程，但推导出的N-S 方程与风环境模拟中常用的方程形式有所差异［12-14］，从而产生模拟误差。该误差与模拟时间步长δt的设定紧密相关，不恰当的δt设置可能导致计算结果出现压缩性误差或数值振荡。目前，在应用LBM-LES模拟风环境问题时，δt的设置引起的误差问题尚未引起足够重视和充分讨论。为了在应用LBM-LES 模拟风环境时对如何设置δt提供依据，本文梳理了既往研究，从理论方面系统总结了δt的设置可能引起的压缩性误差或数值振荡，并以室内空气流动案例为例，定量讨论了δt造成压缩性误差或数值振荡的程度。

1 含BGK的LBM中与时间步长相关的误差理论分析与总结

1.1 含BGK的格子玻尔兹曼方程及LBM-LES 方法的理论回顾

本节首先对含BGK 碰撞算子的格子玻尔兹曼方程及LBM-LES 方法的理论进行简要回顾，以便后文对误差进行理论分析。该方程如式（1）所示。

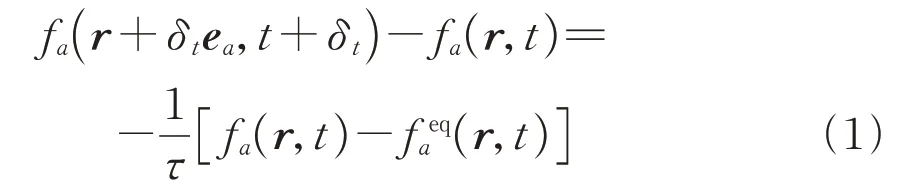
式中：fa为a方向分布函数；ea为a方向上fa的离散速度；r和t分别为fa所在位置向量和时间为fa的平衡函数；δt为离散时间步长；τ为fa的松弛时间。

格子玻尔兹曼法方程在微观层面描述了流体粒子的分布函数随时间发展的演化过程。当分布函数确定后，流体速度u、密度ρ及压力p等宏观物理量可通过式（2）求得。其中，es为格子声速，在三维问题中的值为，其他参数含义同前。

在面对高雷诺数Re 的湍流问题时，可基于LBM 开展LES 计算（LBM-LES）。根据LES 理论，流体的总粘性νtot由分子粘性ν及亚格子粘性νsgs共同构成（即νtot=ν+νsgs）［15］。同时，基于LBM 理论，流体的总粘性νtot与总松弛时间τtot存在如式（3）所示的关系：

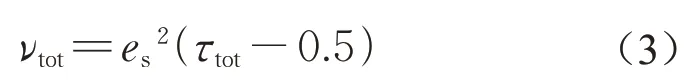
基于式（3）可用总松弛时间τtot替换式（1）中的松弛时间τ以开展LBM-LES 计算。与传统FVMLES 相同，只需采取合适的LES 亚网格模型计算亚网格粘性νsgs，即可开展LBM-LES计算。

1.2 实际物理量到格子玻尔兹曼单位的转换

在式（1）中，以真实物理量（通常包含量纲）所度量的流体原型问题首先被映射到格子玻尔兹曼单位的物理量（通常是量纲一的）进行模拟，模拟完成后再将其映射回真实物理量以输出结果。故模拟第一步是确定适当的转换参数。在无外力等温流体问题中，LBM主要关注流体粘性ν、速度u、压力p及位置r参数，在进行上述物理量的转换时只需网格分辨率δx和时间步长δt两个转换参数。各物理量转换关系如式（4）所示，其中上标ph 和lb 分别表示真实物理量及其对应的格子波尔兹曼单位物理量。

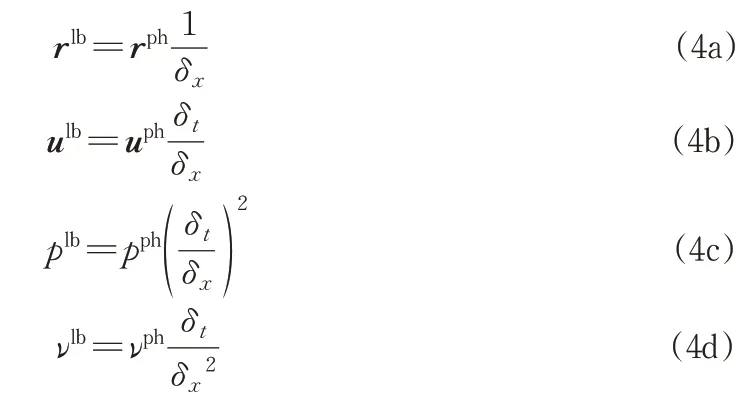
其中，网格分辨率δx通常根据湍流复杂度、模拟所需精度及计算量共同确定，与传统FVM-LES 基本相同。需要注意的是，LBM中采用的是均匀正立方体网格，无法如FVM-LES 一样在局部复杂湍流区域加密网格，故应注意使用测试网格独立性等方式来确定网格尺寸。这在既往研究中已得到多次验证［2，4］。而时间步长δt的确定则与FVM-LES有较大差异。过大或过小的δt都可能导致明显的精度误差，这将是本文接下来的讨论重点。

1.3 压缩性误差

利用BGK算子，可从格子玻尔兹曼方程中推导出形如式（5）的N-S方程［14-15］：

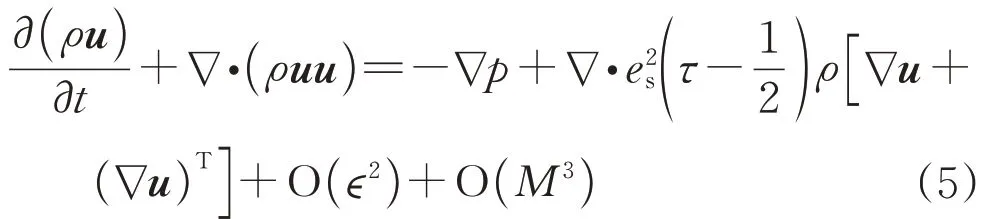
式（5）中：O(ϵ2)和O(M3)分别为与ϵ2和M3相关的高阶省略项；ϵ为努森数（Knudsen number），与马赫数M成正相关，即O(ϵ2)～O(M2)［12］。式（5）相比标准的N-S 方程多了与M相关的附加项。其中M是以格子波尔兹曼单位定义的，如式（6）所示：

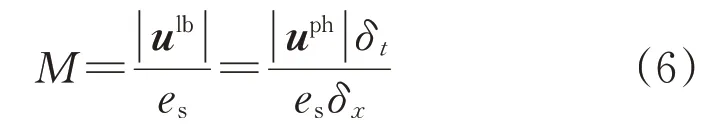
式中：|uph|为局部物理速度uph的大小。

式（5）同时表明，推导出的N-S方程以可压缩形式存在（即无法消去各项中的密度ρ），意味着LBMLES在处理不可压缩流体问题时本质上是一种伪可压缩方法，并会产生所谓的“压缩性误差”［12］。虽然严格来说不可压的流体并不存在，但在处理诸如建筑与城市风环境等低流速问题时，FVM-LES 通常采用不可压缩的N-S 方程。由此可见LBM-LES 与FVM-LES 在计算时针对是否可压缩的处理方法上有较大区别。既往研究［12，15］表明，LBM 的压缩性误差包括与密度梯度相关的误差，以及上述与M相关附加项导致的误差。

式（6）表明，即使在局部风速与网格分辨率δx一定时，较大的时间步长δt会增大M，从而增大使式（5）中与M及ϵ相关项的值（即压缩性误差）。故在模拟不可压缩湍流问题时，与传统FVM-LES相比，不恰当的δt可能导致M增大，从而使得模拟结果产生压缩性误差。Skordos［16］曾尝试用LBM模拟层流状态下的二维泰勒涡旋流和剪切流，发现涡旋流的模拟值和解析值之间的误差随着M的减小而减小，并最终实现稳定收敛。而在剪切流中，随着M的减小，模拟误差呈先减小而后增大的趋势。Reider 等人［12］从理论上推导了压缩性误差，并证实在Re=100且周期为2π的衰减泰勒涡流模拟结果准确性随着M的降低而提高。

应当注意，BGK 算子中的压缩性误差与FVMLES中库朗数C的不正确设置引起的误差并非同一概念，尽管C也是由δx和δt间的取值关系造成。在FVM-LES中，在处理低M不可压缩流体时，通常建议选择适当的时间步长δt以将C控制在小于1（即C= ||uph＜1），否则将造成结果误差甚至模拟发散。而在LBM-LES 中，保证模拟稳定性的一个必要条件是M＜1，即|ulb|＜1 3 ≈0.577，否则模拟将直接发散。故若要保证LBM-LES 模拟正常稳定进行，则必有C= ||ulbδlbt δlbx＜1 始终成立（因为LBM规定了δlbt=1和δlbx=1）。

1.4 超松弛与数值振荡

从式（1）中可明显看出BGK算子的本质是表现分布函数fa(r，t)以一定的速率向平衡分布状态feqa(r，t)的演化过程，即松弛过程。该式可改写为如式（7）的形式：

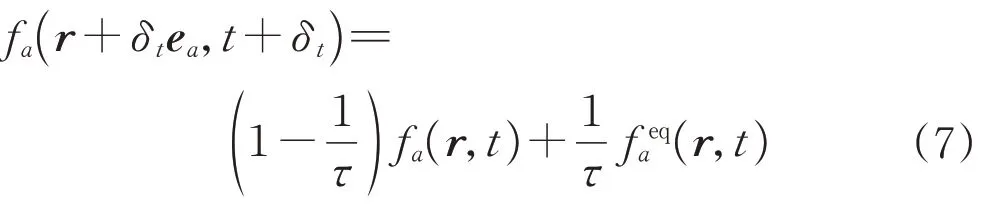
应当注意，τ不可小于因为根据式（3），流体的粘性不可为负。Krüger 等人［17］研究了初始条件为f0feq0=1.1、且feq0为恒定值条件下的BGK 算子，得到了如图1 所示的f0与feq0的关系，对应了上述的三种形态模式。

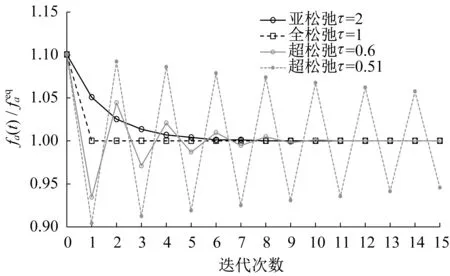
图1 BGK 算子中的亚松弛、全松弛及超松弛算例（重绘自Krüger等［17］）Fig.1 Example of under, full, and over relaxation in BGK collision(reproduced from Krüger et al[17])

图1 表明理想的碰撞过程是亚松弛或全松弛，即fa平滑地或直接向feqa演化。在实际模拟中，全松弛难以达到，因为不可能经过一步就完成模拟。而在超松弛中fa将围绕feqa振动并以指数幅度衰减，最后达到feqa。但τ过小可能导致振动过于剧烈，fa无法达到feqa，最终得到错误结果。

综合式（3）、式（4）可得到如式（8）的关系：

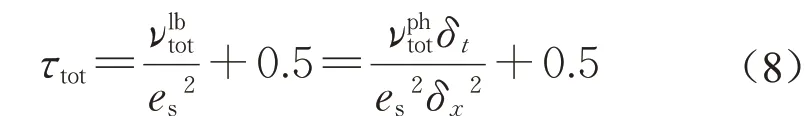
式（8）表明，由于流体粘性νphtot通常为定值，故当确定网格分辨率δx后，τtot的大小与δt正相关。δt的设定影响τtot的大小，从而决定了碰撞过程的松弛模式。理想状态下τ应不小于1，据式（8）可知需要或然而这在风环境模拟中较难满足。由于空气动粘性系数极小（数量级为10-5m2·s-1），即使在LES 计算中加上亚网格粘性νsgs也很难大于例如，在风环境模拟中，由于库朗数和计算量的双重限制，很难在设置δx=1 m 的同时使得δt=10-5s；也无法使用δx=10-3m 来匹配δt=10-1s。尽管在风速较小的局部区域可能满足但建筑或城市尺度的风环境中，大部分区域（特别是所关注的区域）主要以高雷诺数湍流为主，故风环境模拟中BGK 算子主要表现为超松弛模式。通常这种超松弛模式下的振动类似湍流脉动，然而不恰当的网格分辨率δx和时间步长δt之间的关系会导致类似图1中τ=0.51 所示的剧烈振动，最终导致模拟结果产生数值振荡。尤其是在相同的网格分辨率δx下，过小的δt会导致νlb过小，从而导致严重的数值振荡。这与传统的FVM-LES具有极大的不同。

综合上述分析可知，在LBM-LES 进行风环境模拟时，当δx确定后，过大的δt可能导致与M相关的项产生较大的压缩性误差，而δt过小则使松弛时间τ减小，可能造成松弛碰撞算子产生数值振荡。这是LBM-LES 相比传统FVM-LES 在模拟设置上的一个重要区别。FVM-LES 中，只要离散时间步长满足C＜1 则不会对模拟结果产生显著的影响。既往研究已经讨论了层流状态下二维流动中LBMLES 的压缩性误差［12］，而以风环境模拟为代表的湍流状态下不同时间步长对模拟结果的影响尚未充分讨论。下节将以室内气流为例定量讨论这一问题。该案例边界条件相对简单、纯粹、易于控制，便于进行定量研究。

2 等温室内气流模拟案例

本文采用国际能源机构推荐的标准等温室内气流案例（IEA-Annex 20［18］），对含BGK 算子的LBMLES进行压缩性误差研究。该案例形状及取样位置如图2 所示，房间特征参数为L H=3，h H=0.056，r H=0.16。其中L，W和H分别代表房间长度、进深和高度，且H=3.0 m。h和r分别代表气流入口及出口高度。由房间高度及气流入口速度定义的Re≈89 000。模拟参数详表1。本文中，含标准Smagorinsky 亚 网 格 模 型［19］及BGK 碰 撞 算 子 的LBM-LES 应用于本模拟。Han 等［2］的既往研究已经表明该亚网格模型和BGK 算子能较好地适应室内气流模拟，取得满意的模拟精度。

表1 模拟参数及相关边界条件Tab.1 Simulation parameters and boundary conditions

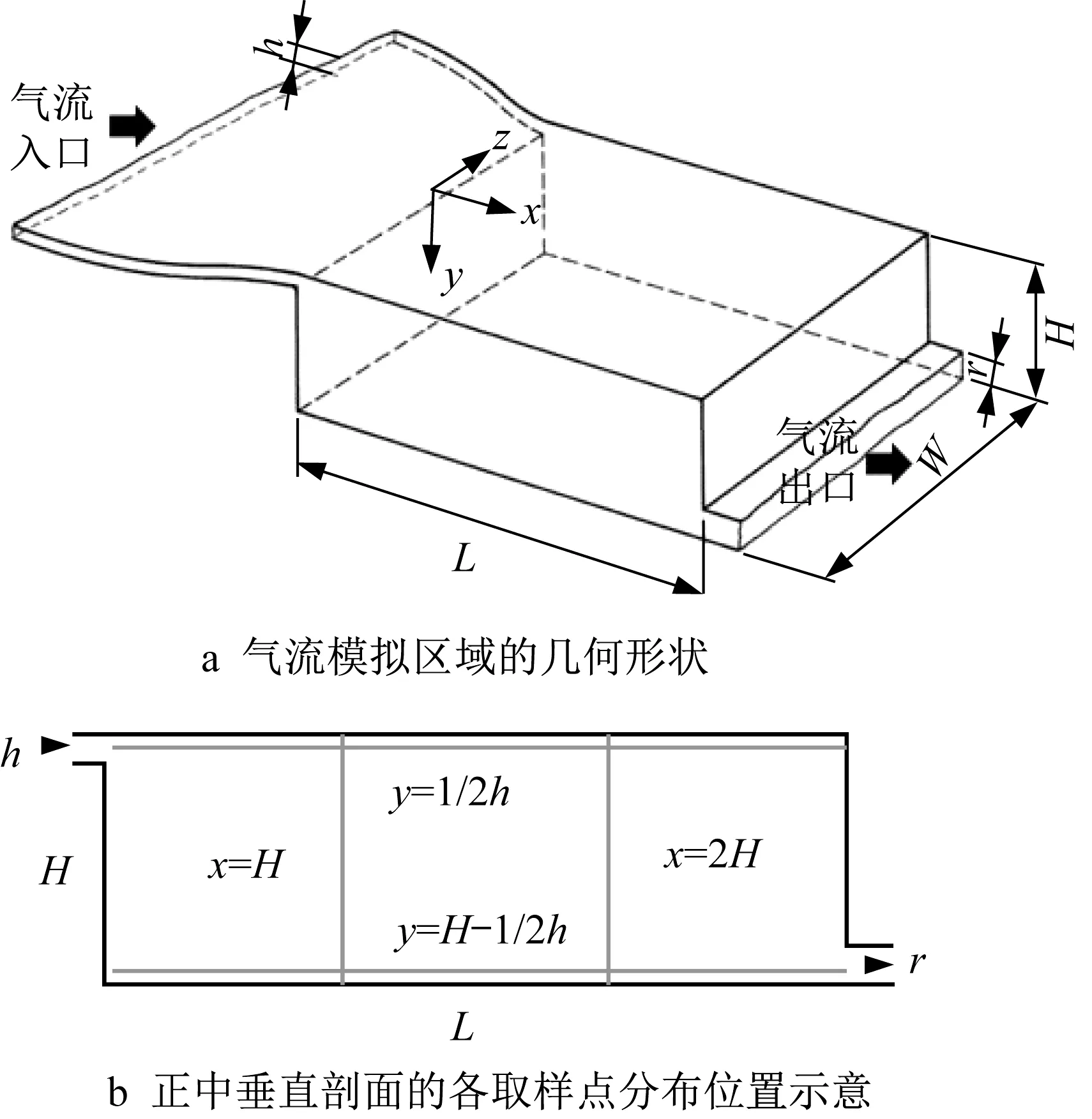
图2 等温室内气流案例的几何形状及取样点分布（修改自IEA-Annex 20［18］）Fig.2 Geometry and sampling points distribution of isothermal indoor airflow case (modified from IEA-Annex 20[18])

之前Han 等［2］已经讨论了LBM-LES 的网格分辨率对模拟精度的影响，本文基于其研究结果仅选取δx=1 75H及1 150H两种网格，讨论不同时间步长δt对模拟精度的影响。具体工况设置如表2所示。工况名称规定为“XaTb”，表示网格分辨率及时间步长分别为δx=H a及δt=1bs。

表2 工况设置Tab.2 Case settings

3 模拟结果与讨论

3.1 平均与湍流脉动风速结果及精度分析

图3 显示了uˉ（时间平均风速的x方向分量）和基于时间平均的脉动风速标准差的x方向分量）的模拟结果。所有结果均用入口风速Uin进行量纲归一化。图中添加了Nielsen 等［21］的实验数据用于验证模拟的准确性。

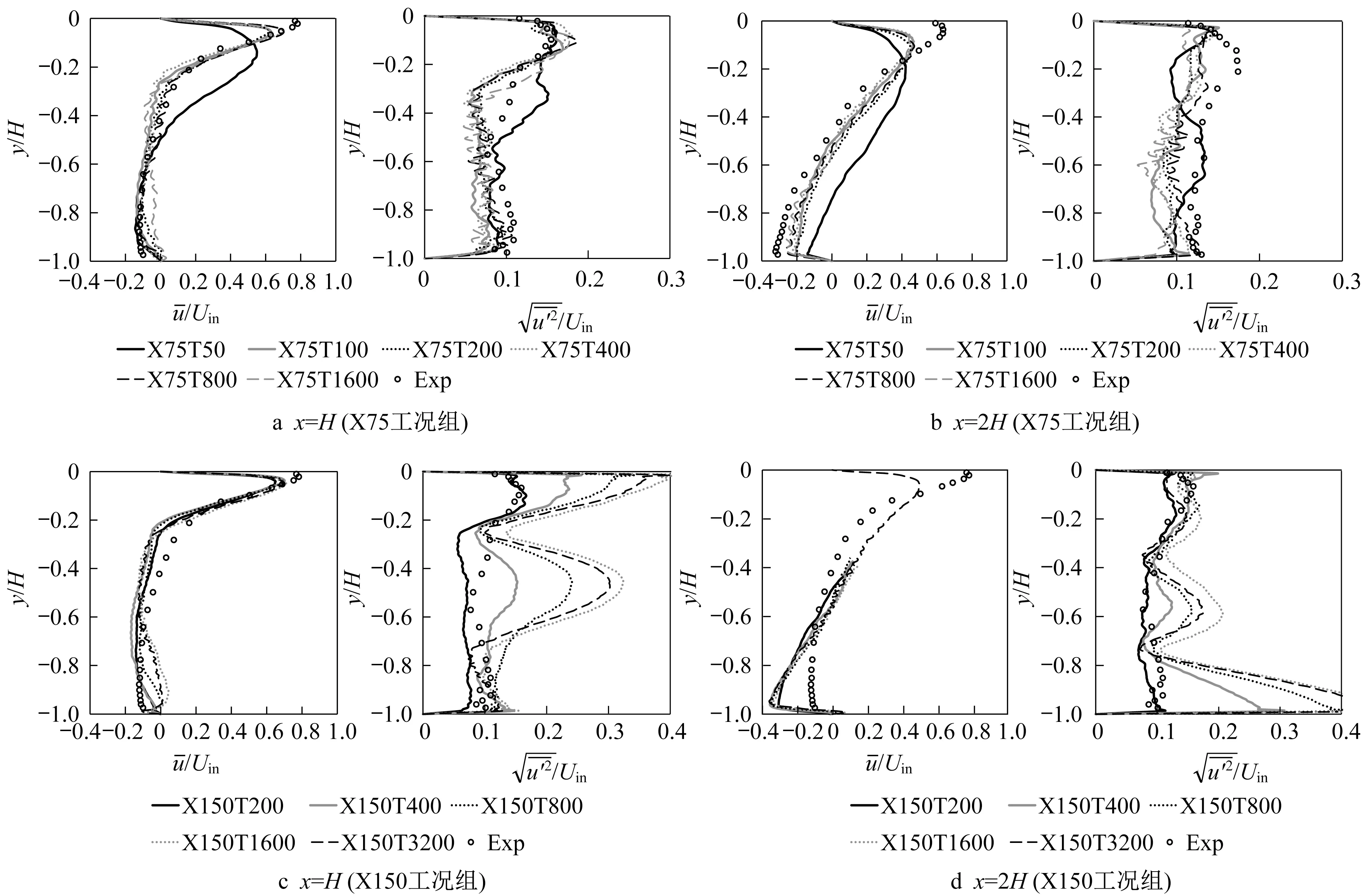
图3 部分区域与的量纲一化模拟结果与实验结果对比Fig.3 Comparison of simulation and experiment results of normalized andin some regions

除精度最低的X75T50，几乎所有工况模拟结果均能再现uˉ和的分布趋势，且模拟精度有随着δt的减小而提高的趋势。X75T800和X75T1600中，和均出现了轻微的空间数值振荡。而在X150工况组中，X150T200 的和都达到了最佳精度。随着δt的减小，精度并未提高，反而出现了明显的数值振荡，从而降低模拟精度。

本文采用式（9）所定义的L2误差范数［17］εq定量评估模拟精度。式中qEXP(r)和qLBM(r)分别代表实验和模拟中位置r处的物理量q。L2 误差范数考虑了Nielson 实验数据的所有点。εq越小代表模拟与实验之间的误差越小，从而模拟精度越高。

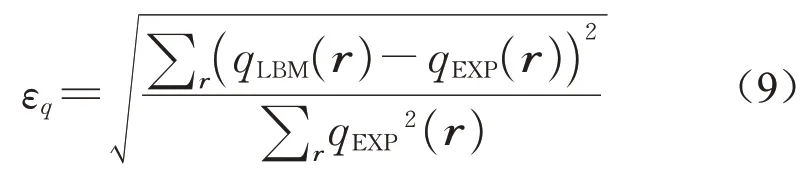
图4显示了不同δt时所有工况的L2误差范数变化曲线。随着δt从1/50 s 减小到1/200 s，X75 工况组中和的误差均减小，随后则显著增大。可以推测，δt从1/50 s 减小到1/200 s 时的精度提升可能是由于压缩性误差的减小；而δt＜1/200 s时精度降低应该是由于超松弛导致，因为在这些工况中观察到了和的数值振荡。对于X150 工况组，δt=1/200 s 时，模拟精度最高，而后随着δt的减小的模拟精度迅速衰减，这也应归因于超松弛引起的振荡。3.2和3.3节将深入讨论这些推测。

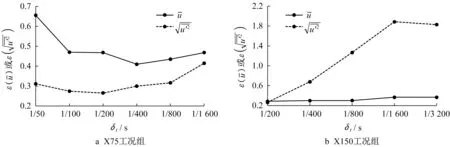
图4 不同δt的模拟精度L2误差范数变化曲线Fig.4 L2 error norms of different δt values

3.2 压缩性误差的讨论

X75T50、X75T100 和X75T200 这三个工况的模拟精度有较大差异，但其风速模拟结果并未显示出明显的数值振荡，且三者的网格设置完全一致仅δt不同。这表明它们的精度差异极有可能是由于不同δt导致的压缩性误差所引起，于是本节选择这三个工况分析压缩性误差。

图5显示了三个工况中各区域的时间平均密度ρˉ与初始值ρ0相比的相对偏差()-ρ0ρ0。如1.3节所述，LBM-LES 是一种伪可压缩模拟方法，即使在模拟同一个不可压缩问题时，不同的δt设置亦会导致密度变化显著。X75T50的δt较大，导致ρˉ明显偏离了初始值，尤以入口附近区域更为明显。

图6显示了所有工况中整个模拟域的空间平均密度相对于初始值的偏差。该偏差反映了LBMLES 计算中密度的压缩程度。随着δt减小一半，空间平均密度的差异几乎呈指数衰减。当密度偏差小于0.5 %后逐渐达到稳定。此时的密度接近初始值，可忽略压缩性的影响。

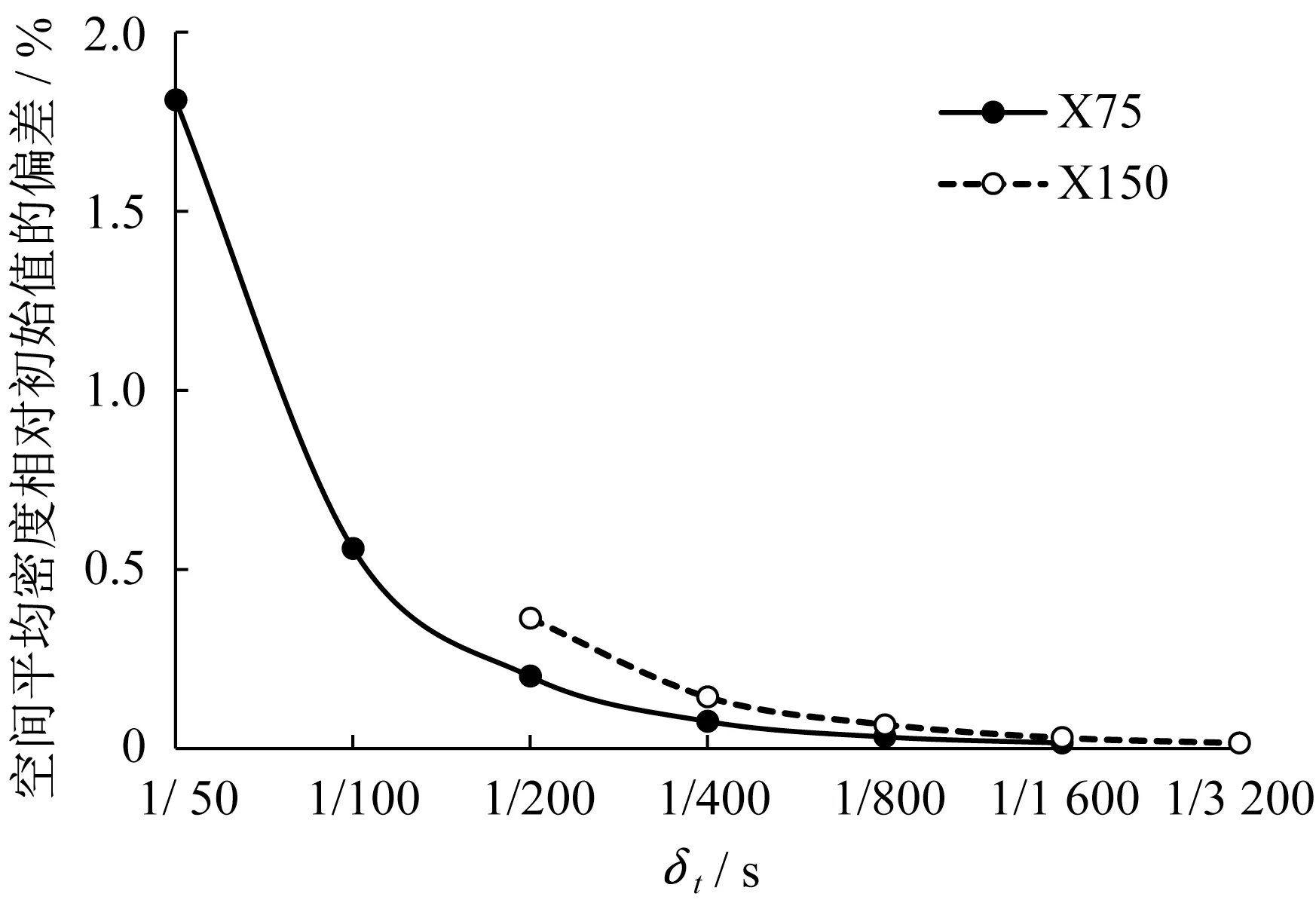
图6 所有工况中全空间平均密度与初始值的相对偏差变化Fig.6 Deviation between spatial-averaged density and initial value of all cases

垂直截面上量纲一化uˉ及M的计算结果如图7所示。在X75T50 中，来自入口的气流有远离天花板向下的趋势，导致该区域的模拟结果精度较差。据图7b所示，该区域M大于该工况其他区域及其他工况的M，并超过了0.3。这与Krüger 等［17］的研究一致。该研究建议LBM-LES模拟场中的由ulb定义的M不应大于0.3，否则将产生较显著的压缩性误差。同时，图5 显示该区域密度变化剧烈。这再次表明较大的密度梯度将会导致显著的压缩性误差。随着M的降低，入口处的气流趋于水平，表明压缩性误差可通过降低M得到一定的补偿。X75T50的其他区域或其他工况中M均小于0.3，故可忽略uˉ的压缩性误差。同时，X150工况组中M＜0.3始终成立，表明X150 工况组的压缩性误差均不明显，因而X150 工况组中模拟精度并未随着δt的降低而提高。

图5 部分工况的中央垂直平面量纲一化时间平均密度偏差( -ρ0 )ρ0分布Fig.5 Deviation of time-averaged density(-ρ0 )ρ0 at central vertical section in some cases

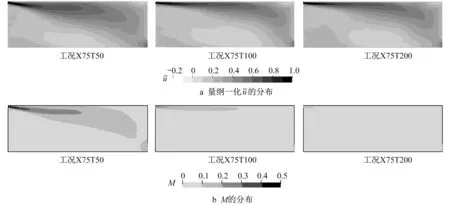
图7 部分工况中垂直截面上量纲一化uˉ及M分布Fig.7 Vertical distribution of normalized uˉand M of some cases

以上讨论证实，在使用LBM-LES 求解室内湍流时，过大的M会导致速度场产生明显的压缩性误差。通过调整δt可减小M，以补偿误差。为了减少压缩性误差造成的影响，应尽量保证流场中最大风速区域的M＜0.3，即值得注意的是，M是由ulb定义的格子玻尔兹曼单位的参数。即使模拟问题原型相同，也可以通过使用不同的δt改变M，这与物理场中由真实速度定义的M不同。

3.3 超松弛导致的数值振荡讨论

3.1 节 图3 显 示，在X75T400、X75T800、X75T1600工况和X150工况组中的大多数工况中均观察到明显数值振荡，这可能由于超松弛碰撞模式造成，本节将对此进行分析。图8 显示了所有工况的f0在点(x，y，z)=(H，H/2，H/2)处当流场达到充分发展后某个1 s 周期（第1 080～1 081 s）内的松弛状况。选择点(x，y，z)=(H，H/2，H/2)是因为在该点处X75T50、X75T100 和X75T200 中没有明显的振荡，而在其他工况中发生振荡，即存在一个振荡发生的临界状况。图中f0(t)/f0eq(t)表明某一t时刻f0与f0eq间的大小关系

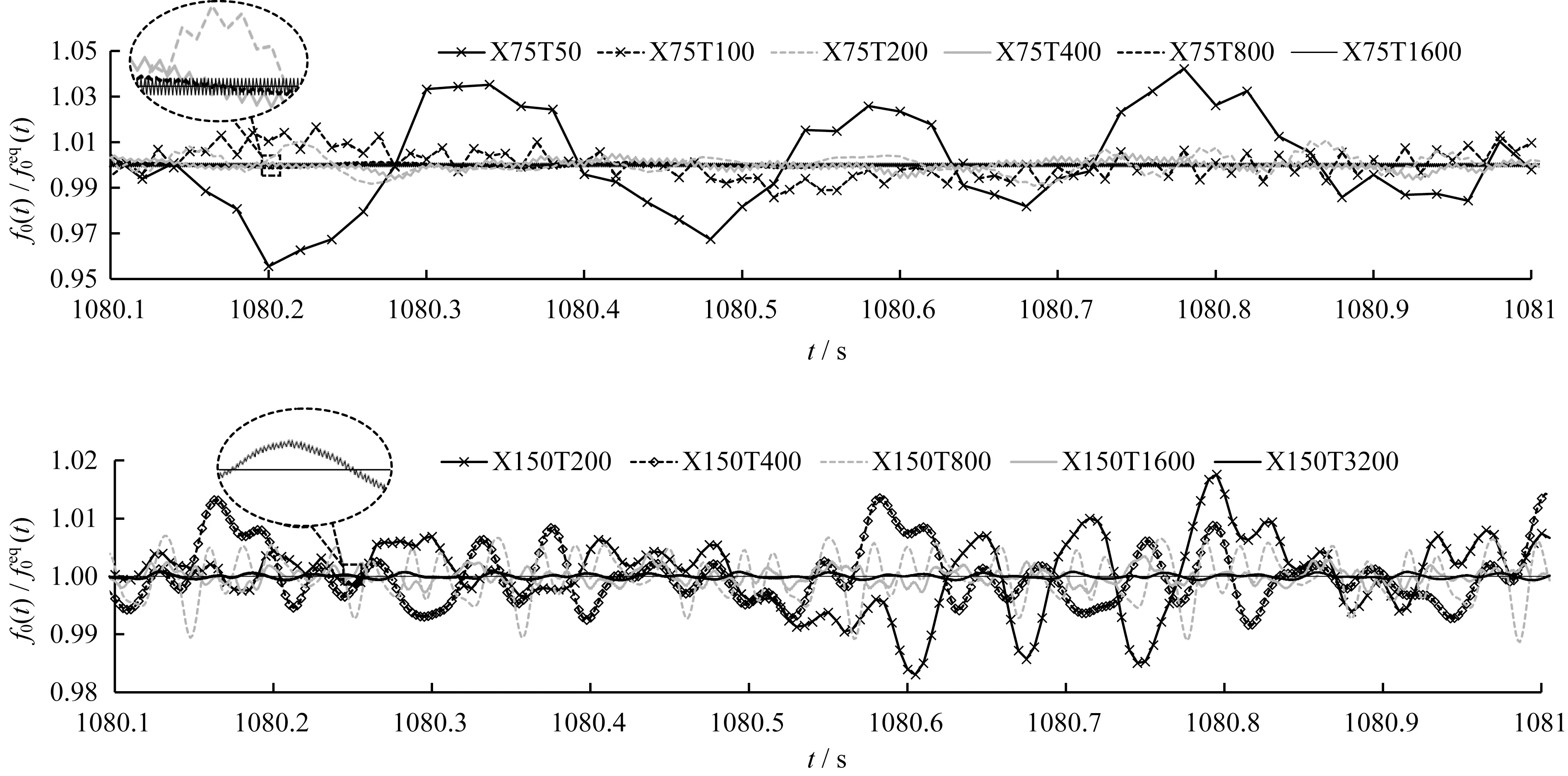
图8 所有工况在(x，y，z)=(H，-H/2，H/2)位置处1 s内f0的超松弛现象Fig.8 Over relaxation phenomenon in one second at(x,y,z)=(H,-H/2,H/2)of all cases

在所有工况中，f0围绕f0eq来回摆动，表明所有工况都是超松弛碰撞模式，而不是理想的亚松弛模式，此时f0并不向f0eq呈指数衰减。这一结果证实了在湍流中，超松弛碰撞模式比亚松弛更常见。在X75 工况组中，f0摆动的“频率”随δt的减小而增大。同时摆动“幅度”随δt减小而减小。从X75T50 到X75T200，摆动过程似乎没有形成数值振荡，而应该是由湍流脉动导致。然而在X75T400、X75T800 和X75T1600 中，摆动过程演化为可见的高频振动，与速度场的模拟结果发生数值振荡的状况一致。类似地，在X150组中，当δt降低到一定程度时，分布函数形成了高频振动，最终形成了速度场发生数值振荡，这在X150T1600至X150T3200之间尤为明显。

由此可见，当δt减小到一定程度时，超松弛碰撞模式所对应的湍流脉动会最终演化成分布函数的高频振动，并最终导致宏观速度场的数值振荡。然而，超松弛碰撞模式何时演化为高频振动则较为复杂，其与局部湍流的流动模式、网格尺寸、流体性质及碰撞算子等都有很大关系，并非只与δt线性相关，故较难判断数值振荡的临界δt。一般建议在消除压缩性误差的前提下尽量增大δt以避免数值振荡。

4 结论

本文分析并总结了采用含BGK 碰撞算子的LBM-LES模拟风环境问题时，时间步长δt对模拟精度的影响，并以室内气流模拟案例对其进行了定量讨论。主要结论如下：

（1）LBM-LES 是一种伪可压缩方法，在处理不可压缩问题时模拟域中的密度在模拟过程中会发生变化。过大的δt会使得密度变化较大，导致速度场产生压缩性误差。较小的δt可以减小压缩性误差。

（2）在模拟湍流时，BGK 碰撞算子通常表现为超松弛碰撞模式，即分布函数表现为一定程度的摆动。过小的δt会导致摆动会演化成高频振动，最终使得速度场发生数值振荡。该现象在网格分辨率相对较高时更容易产生。

（3）在确定网格分辨率（如网格独立性测试）后，δt应足够小以满足最大风速区域M＜0.3（即δt≤以减小压缩性误差。在此基础上尽量采用较大的δt以防止数值振荡的发生。

本文仅粗略确定了δt的取值上限，今后的工作将着重于如何确定δt的合理范围，并建立δt与其他物理量之间的定量关系。此外，对应于风环境中高Re 问题的模拟，通常采用比BGK 更为复杂、鲁棒性更高的碰撞算子（如MRT、cumulant LBM 等），δt的变化对这些碰撞算子的影响也应予以进一步研究。