基于Nelder-Mead算法的机器人主动嗅觉室内时变污染源定位

周晅毅，王富玉，杨流阔，顾 明

（同济大学土木工程防灾国家重点实验室，上海 200092）

当有害气体在室内释放后，会迅速恶化空间环境，危及人员健康，甚至造成严重的生命财产损失［1］。因此快速准确地反演污染源参数，尤其是定位污染源的位置，对保障人员安全，减轻财产损失，实现“韧性城市”具有重要意义。按照不同的传感器布置形式，污染源参数反演方法主要分为两类［2］：固定传感器法和移动传感器法。其中固定传感器法分为以下4种方法［3］：准（伪）可逆方法［4-5］、优化算法［6］、正则化方法［7-8］以及基于概率的方法［9］。移动传感器法又称为机器人主动嗅觉，是利用搭载测量浓度或其他物理量传感器的移动机器人，对区域内的污染源进行动态搜索，其分为以下4种方法［10］：基于梯度算法［11］、仿生算法［12］、基于概率和地图算法［13］以及多机器人算法［14］。

基于梯度算法的优点是易于实现，缺点是高度依赖浓度梯度。当流动复杂尤其是存在湍流时，机器人在定位过程中由于难以捕捉到浓度梯度的变化，容易导致定位失败。仿生算法的优点是计算成本通常较低，不足之处是难以将单个机器人的仿生算法推广到多机器人上［10］。基于概率和地图算法的优点是结果直观，可以得到关心区域的浓度地图或概率云图，然而其计算量较大且高度依赖硬件。多机器人算法相比于基于梯度算法，可以应用于更复杂的场景；相比于仿生算法，各机器人之间可以共享信息、互相协作；相比于基于概率和地图算法，无需对搜索区域进行遍历，计算量小且对硬件要求不高。因此，多机器人算法在近几年受到了广泛关注［15］。

前人利用机器人主动嗅觉主要集中在对稳态污染源进行定位研究，且大部分研究假设室内无障碍物。然而在实际情况中，污染物的释放速率一般不会保持恒定，且室内往往存在障碍物。时变的污染源意味着浓度分布是实时变化的，尤其当存在障碍物时，其会对流场产生干扰，这使得污染物的浓度分布更加复杂。这些因素给污染源定位工作带来了新的挑战。本文以二维室内空间为研究对象，将NM（Nelder-Mead）算法与机器人主动嗅觉中的多机器人算法相结合，对衰减型和周期型两种不同的时变污染源开展定位研究。同时设置两个障碍物，并应用相应的避障算法对其规避。最后对可能影响定位成功率的因素展开讨论，为实际应用提供了参考依据。

1 机器人主动嗅觉算法

机器人主动嗅觉定位污染源的过程主要分为三个阶段［16］：第一阶段是寻找污染物羽流，该阶段采取“Z”字形运动以提高搜索效率［16］；第二阶段是污染物羽流追踪，寻找到污染物羽流后，采用NM算法对其追踪；第三阶段是污染源声明，若机器人的最终位置在污染源半径0.5 m以内［17］，则视为定位成功，此时机器人进行声明，定位工作结束。此外，若搜索空间内存在障碍物，还要应用相应的避障算法。

NM 算法是一种求解极值的算法，其原理是利用各机器人组成单纯形，通过反射、扩张、压缩及整体收缩等步骤，不断构成新的单纯形来优化位于浓度最低处的机器人，从而使整个机器人群体逐步逼近真实污染源。该算法的优点是收敛速度快，局部搜索能力强，其具体步骤如下［18-19］：

（1）反射：首先在搜索区域内初始化n+1 个机器人，这些机器人的位置记为x1，x2，...，xn+1，每个机器人所对应的污染物浓度记为f1，f2，…，fn+1。通过计算，找到这n+1 个机器人中的浓度最高值fH，以及与之对应的机器人位置xH；浓度最低值fL，以及与之对应的机器人位置xL。通过对浓度最低位置xL进行反射，生成反射点xR，与之对应的浓度值记为fR。若fL≤fR≤fH，则xR替代浓度最小点xL，组成新的机器人群；

（2）扩张：若fR＞fH，则沿反射方向对机器人进行扩张至xE，与之对应的浓度值记为fE。若fE＞fR，则xE替代浓度最小点xL，组成新的机器人群；反之，xR替代浓度最小点xL，组成新的机器人群。扩张的目的是算法认为反射方向是靠近污染源的方向，机器人应朝该方向继续移动；

（3）压缩：若fR＜fL，则对反射点xR压缩至xS，与之对应的浓度值记为fS。若fS＞fL，则xS替代浓度最小点xL，组成新的机器人群；反之，舍弃当前压缩点xS，重新进行压缩。对浓度最小点xL压缩至x′S，与之对应的浓度值记为fS′。若fS′＞fL，则x′S替代浓度最小点xL，组成新的机器人群。压缩的目的是算法认为反射方向是远离污染源的方向，机器人应朝相反的方向移动；

（4）整体收缩：若fS′≤fL，则除xH以外的所有机器人进行整体收缩，组成新的机器人群：xi=xH+δ(xi-xH)，0 ＜δ＜1，i=1，2，…，n+1且i≠H。式中：δ=0.5［19］为整体收缩系数。整体收缩的目的是算法认为反射是错误的，污染源可能位于当前机器人所组成的单纯形内，故所有机器人整体向内移动来靠近污染源。

对NM算法进行循环，直到达到最大搜索步数或某个机器人成功定位到污染源。在该过程中，若机器人某步搜索时遇到了障碍物，则暂停循环NM算法，先采用避障算法规避障碍物，随后从第1步开始重新进行循环。机器人避障算法原理如文献［20］所述。

2 计算及求解设置

2.1 研究对象

如图1 所示，以简化的二维室内空间为研究对象，长（x）为12 m，宽（y）为8 m。内部有两个边长为1.5 m的矩形障碍物，在左侧上下位置分别设有宽为0.4 m的排气扇，作为进风口，风速为0.8 m·s-1。右侧中间位置设有宽为0.4 m的出风口。污染源位于室内中心处（x= 6 m，y= 4 m），排污口为边长0.05 m的正方形。

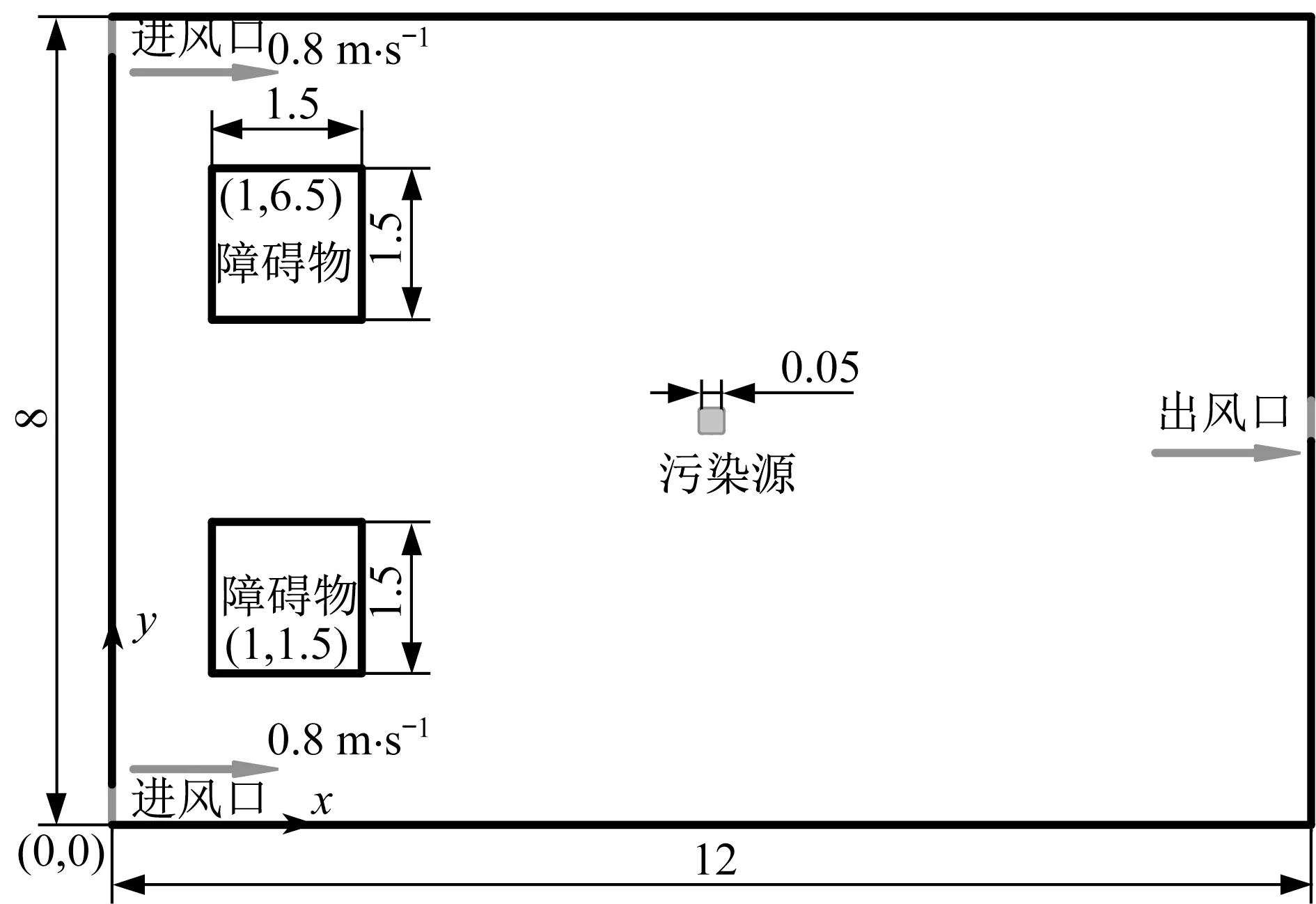
图1 室内空间示意图（单位：m）Fig.1 Schematic diagram of indoor space (unit:m)

2.2 CFD模拟设置

在 ANSYS/Fluent 中，首 先 采 用 RANS（Reynolds-averaged Navier-Stokes）模型得到室内的稳态流场，然后在该稳态流场的基础上，采用URANS （unsteady Reynolds-averaged Navier-Stokes）模型对时变污染源的释放过程进行模拟。选取乙烯（C2H4）作为污染源，其密度与空气几乎一致且物理性质稳定。两种时变污染源分别为：衰减型污染源，u=u0e-t/40；周期型污染源，u=0.5[u0cos(2πt/T)+1]。式中：u为污染物释放速率，m·s-1；u0=1 m·s-1，为初始释放速率；T=20 s，为周期型污染源释放周期。两种污染源释放速率随时间的变化曲线如图2所示。

图2 时变污染源释放速率随时间变化曲线Fig.2 Time-variant contaminant sources release rates over time

采用高精度的结构化网格，其增长率小于1.08，总数为78 932。网格在进风口、出风口、障碍物和污染源处均进行了加密，最小网格尺寸为0.02 m。在数值模拟中，网格精度需要足够高，以保证结果的稳定性和可靠性。本文采用了三种网格方案进行网格无关性检验：基本网格总数为78 932（表1）；细网格总数为106 390，其中最小网格尺寸为0.01 m；粗网格总数为45 873，其中最小网格尺寸为0.025 m。污染物的平均质量分数是衡量污染物浓度分布的关键参数，以周期型污染源为例，通过比较x=5.0 m处三种网格划分方案下污染物的平均质量分数来进行网格无关性检验，如图3所示。

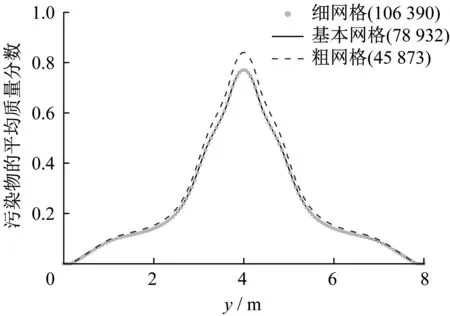
图3 网格无关性检验（x=5.0 m）Fig.3 Grid sensitivity test (x=5.0 m)

由图3 可知，细网格与基本网格的污染物平均质量分数差异不大，而粗网格的结果与前两者相比有一定的偏差。这表明当网格总数大于78 932 时，模拟结果对于网格是收敛的。采用过多的网格进行数值模拟将非常耗时，故本文网格总数定为78 932。详细的参数设置及边界条件如表1所示。

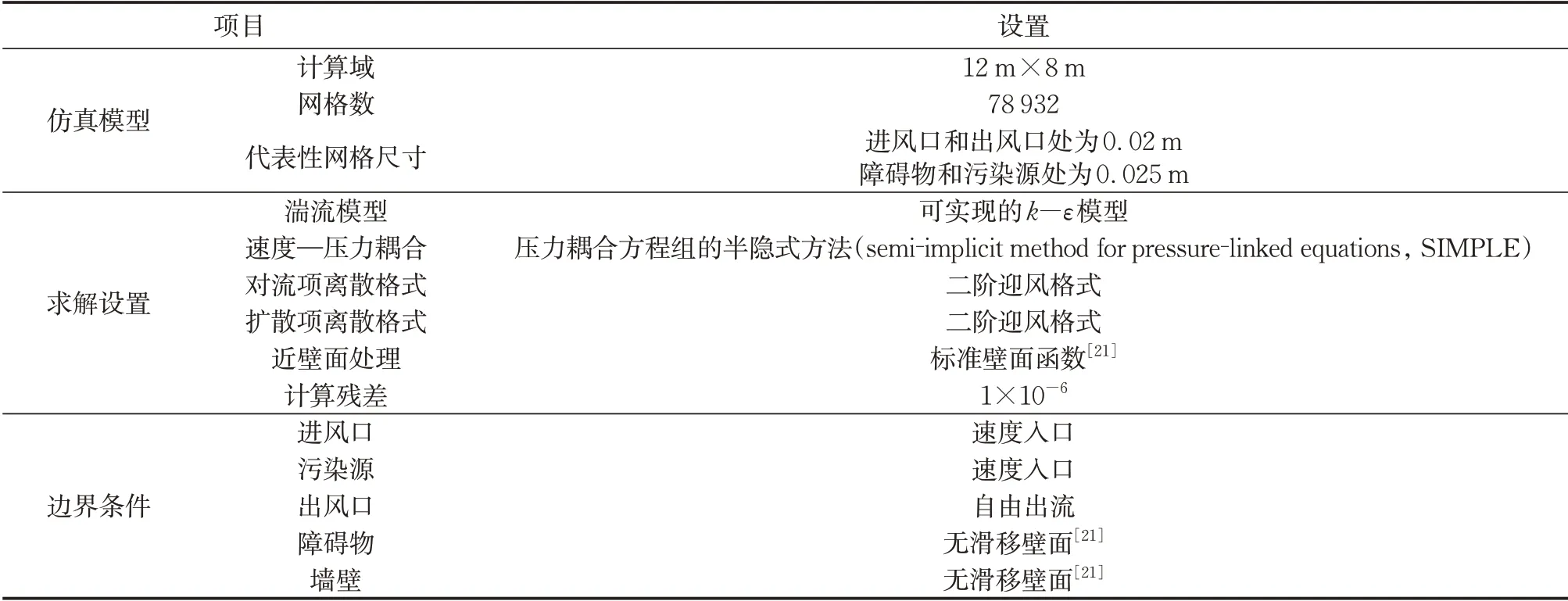
表1 参数设置及边界条件Tab.1 Parameter settings and boundary conditions

3 机器人定位结果

3.1 流场模拟结果

流场是污染物输运的基础，在进风口风速保持常数的情况下，该室内的稳态流场如图4 所示。从图中可见，进风口处由于对流作用明显，在上下两侧分别形成了风速较大的条状区域。在通风和障碍物的共同作用下，污染源后方出现了两个对称分布的旋涡。由后续分析可知，污染物会在流场的作用下不断向左侧输运积聚从而形成局部浓度较大区域，这将对定位工作提出挑战。下文将基于该稳态流场，对两种时变污染源的定位结果进行讨论，并对可能影响定位成功率的因素进行分析。

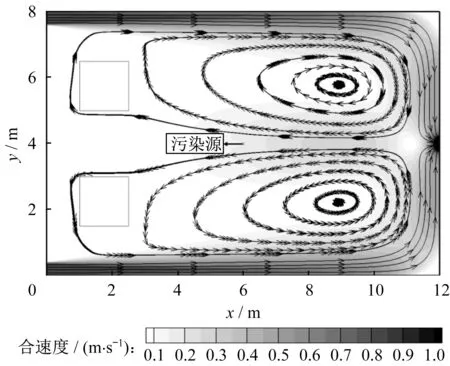
图4 室内稳态流场Fig.4 Steady flow field of indoor space

3.2 衰减型污染源定位结果

由第4节分析结果知，为保证定位效果最好，参与搜索的机器人数量设为5 个、机器人的响应时间设为2 s、最大搜索步数设为50步。以此作为污染源定位的基本设置，来分析两种时变污染源的定位结果。各机器人初始的搜索位置随机分散在室内，其不同时刻的位置如图5所示。

从图5可见，衰减型污染源释放后，空间内污染物的浓度逐渐增加，这段时间有利于机器人定位污染源。然而到40 s时，由图2可知污染源强度已经衰减了一半以上，此时真实污染源附近的浓度值与释放之初相比降低较多，且在通风气流作用下污染源左侧逐渐出现了局部浓度较大区域。随着时间的推移，真实污染源附近的浓度持续降低，局部浓度较大区域继续扩大，并在气流作用下进一步左移远离真实污染源，这给定位工作带来了困难。

图5 衰减型污染源各机器人不同时刻位置Fig.5 Position of each robot at different time in attenuated contaminant source

初始时刻各机器人随机分散在室内，污染物仅集中在污染源附近，其他区域几乎没有污染物。此时机器人采取“Z”字形搜索。20 s时，部分机器人捕捉到了污染物羽流。随后，所有机器人切换至NM算法对污染源进行定位。随着污染物的持续释放，40 s时，所有机器人都捕捉到了污染物羽流。然而，在流场的作用下，真实污染源左侧出现了局部浓度较大区域，在50 s 时，大部分机器人陷入了该区域。一直到60 s，各机器人才逐步离开该局部浓度较大区域，并更加接近真实污染源。最终在80 s时，所有机器人都成功定位到了污染源。

3.3 周期型污染源定位结果

在定位周期型污染源时，同样将参与搜索的机器人数量设为5个、响应时间设为2 s、最大搜索步数设为50 步。各机器人初始的搜索位置随机分散在室内，其不同时刻的位置如图6所示。

从图6可见，周期型污染源释放后，污染源左侧区域在流场的作用下同样出现了局部浓度较大区域，与衰减型污染源定位过程类似，该区域的存在仍会增加定位难度。所不同的是，由于污染源是周期释放的，局部浓度较大区域也会周期性波动，且该区域始终位于真实污染源左侧不远处，几乎不发生左移，真实污染源处仍然是浓度最大的地方，这有利于机器人离开浓度较大区域。因此，周期型污染源的定位难度要小于衰减型污染源。

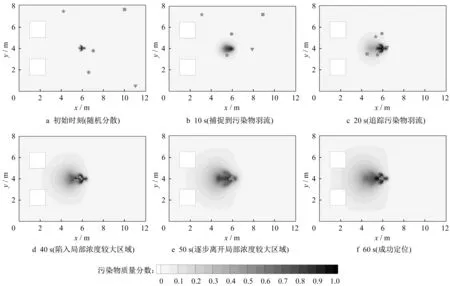
图6 周期型污染源各机器人不同时刻位置Fig.6 Position of each robot at different time in periodic contaminant source

初始时刻各机器人随机分散在室内并采取“Z”字形搜索。10 s 时，某个机器人捕捉到了污染物羽流。随后，所有机器人切换至NM 算法对污染源进行定位。20 s时，随着污染物的持续释放，几乎所有机器人都捕捉到了污染物羽流。然而40 s 时，大部分机器人陷入了局部浓度较大区域。一直到50 s，各机器人才逐步离开该区域。最终在60 s 时，所有机器人都成功定位到了污染源。

4 影响因素分析

图5、图6直观地展示了当参与搜索的机器人数量为5个、响应时间为2 s、最大搜索步数为50步时，利用机器人主动嗅觉对两种时变污染源定位成功的情况。然而在实际应用中，很多因素会影响定位结果，这使得机器人可能不会每次都能成功搜索到污染源。故本文对两种不同的时变污染源进行100次重复定位，并对机器人数量、响应时间和最大搜索步数这三个主要影响因素进行分析，来讨论其对定位结果的影响。在对影响因素进行分析时，仅改变待研究的因素，其余仍与基本设置保持一致。

4.1 机器人数量的影响

若机器人的最终位置在污染源半径0.5 m 以内［17］即视为定位成功，定位成功率计算如下：

式中：Q为定位成功率；Nr为成功定位次数，Nz=100 为定位总次数。当响应时间为2 s、最大搜索步数为50步时，污染源定位成功率随机器人数量的变化情况见图7。

图7 定位成功率随机器人数量的变化Fig.7 Localization success rates versus the number of robots

如图7所示，对衰减型污染源来说，成功率随着机器人数量的增加一直处于下降趋势，且在大多数情况下低于周期型污染源。这与该污染源的释放形式有关，如图2 所示，随着时间的推移，污染源释放速率呈指数型衰减，在40 s 时污染源强度已经衰减了一半以上。同时在通风气流的作用下，污染源左侧形成了局部浓度较大区域，其不断左移并向四周扩散。当机器人数量增多后，相应地搜索步数和搜索时间也会增加，这就导致越来越多的机器人会陷入局部浓度较大区域，从而使整个机器人群体偏离真实的污染源，易导致定位失败。当机器人数量为25个时，成功率已经不足10%。

对周期型污染源来说，也有类似的结论，所不同的是当机器人数量较少时，成功率随机器人数量的增多而增大，当机器人数量为6个时，成功率达到最大值92%。这说明少量增加机器人数量，可以获得更多的浓度信息，使NM 算法能够做出更加准确的判断，从而提高成功率。然而，当机器人数量大于6个时，成功率反而开始下降；当机器人数量为25 个时，成功率已经不足20%。这与NM算法的原理有关，该算法通过反射、扩张、压缩及整体收缩等步骤，不断构成新的单纯形来优化位于浓度最低处的机器人，从而使整个机器人群体逐步逼近真实污染源。当机器人数量较多时，分布在浓度较低区域的机器人数量也会更多，相应地需要更多的搜索步数来改善位于浓度较低区域的机器人。因此在最大搜索步数一定时，过多数量的机器人可能会导致成功率下降。

由此可见，机器人数量过多并不能很好地发挥NM 算法的优势，且在定位衰减型污染源的过程中非常容易陷入局部浓度较大区域。当机器人数量超过5个时，衰减型污染源的定位成功率已不足80%。故通过本文研究，发现机器人数量为5 个时较为合适。此时两种时变污染源的定位成功率均在80%以上。

4.2 机器人响应时间的影响

在实际应用时，由于机器人搭载的浓度传感器存在一定的采样频率，导致无法实时采集浓度信息，且机器人每步移动和分析浓度信息需要一定时间，故实际的定位过程是间断进行的［15］。虽然浓度信息是实时变化的，但是机器人无法做到实时采样和定位，总存在一定的“响应时间”。机器人移动到指定位置所消耗的时间记为t1；移动到指定位置后，传感器开始采集浓度信息，并利用NM 算法对浓度信息进行分析，该过程所消耗的时间记为t2，则每步的响应时间为(t1+t2)。在一个响应时间内，由于无法捕捉到浓度信息的变化，故机器人认为在该时间段内，浓度信息保持不变。响应时间的长短与机器人的硬件性能有关，当机器人数量为5个、最大搜索步数为50 步时，污染源定位成功率随机器人响应时间的变化情况见图8。

如图8 所示，机器人响应时间越短，成功率越高。当响应时间为1 s 时两种时变污染源的定位成功率均接近100%。这是因为当响应时间较短时，机器人能够充分地捕捉到周围浓度信息的变化，从而可以利用NM算法进行更加准确的判断。随着响应时间的增长，成功率明显降低，当响应时间为10 s时，成功率已经不足5%。这是因为响应时间越长，上一响应时间内采集到的浓度较大区域在经历一段时间后可能变为浓度较小区域。剧烈变化的浓度信息无法及时反馈给NM 算法，导致成功率较低。虽然响应时间为1 s定位成功率最高，但考虑到实际应用时机器人难以在1 s内完成移动和采样，故通过本文研究，认为机器人响应时间为2 s 时较为合适，此时两种时变污染源的定位成功率均在80%以上。

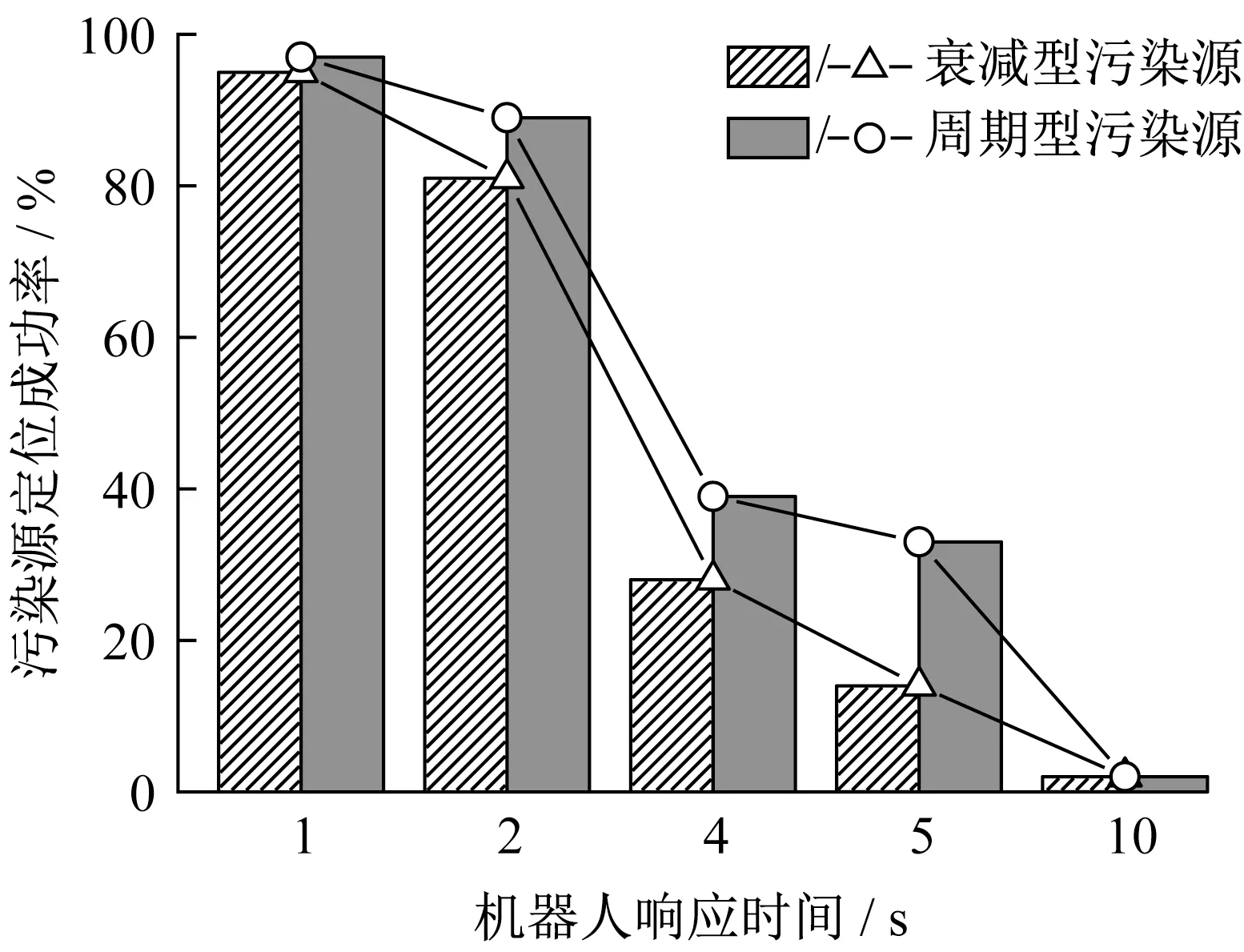
图8 定位成功率随机器人响应时间的变化Fig.8 Localization success rates versus robot response time

4.3 机器人最大搜索步数的影响

在实际应用时，往往需要对机器人设置最大搜索步数［2］，若机器人超过最大搜索步数仍未成功定位，则终止定位并视为定位失败，即机器人不会无限制地移动下去。机器人完成定位时所移动的步数，主要与每次移动的步长大小及初始搜索位置有关。

由NM 算法原理可知，每次移动是以机器人群的形心为参考点，通过反射、扩张、压缩及整体收缩等步骤来完成。由于各机器人初始的搜索位置随机分散在室内，故形心的位置也是随机的；且反射系数α=1［19］、扩张系数γ=2［19］、压缩系数β=0.5［19］及整体收缩系数δ=0.5［19］并不相同，因此机器人每次移动的步长大小不是固定不变的，其与机器人初始群体的规模及各系数的取值有关。此外，机器人完成定位时所移动的步数，还与初始搜索位置有关。若大部分机器人的初始位置远离污染源，则往往需要花费较多的步数才能捕捉到污染物羽流（即完成搜索的第一阶段），此时需要足够的搜索步数才能成功定位；相反，若大部分机器人的初始位置靠近污染源，则相对容易地就能捕捉到污染物羽流，此时只需要较少的搜索步数就能成功定位。因此，机器人最大搜索步数在某种程度上会影响成功率。若设定的最大搜索步数较少且初始搜索位置较为不利时，可能机器人还处在定位过程中，系统就停止了搜索。当机器人数量为5个、响应时间为2 s时，污染源定位成功率随机器人最大搜索步数的变化情况见图9。

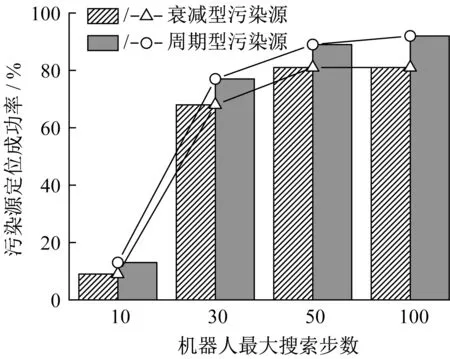
图9 定位成功率随机器人最大搜索步数的变化Fig.9 Localization success rates versus the maximum number of robot search steps

如图9所示，机器人最大搜索步数越多，成功率越高。当最大搜索步数为30步（污染源释放时间为60 s）时，两种污染源的定位成功率均超过了60%，其中周期型污染源的成功率接近80%。对衰减型污染源来说，当最大搜索步数为50 步（污染源释放时间为100 s）时，成功率达到最大值81%，且当搜索步数超过50步时，成功率几乎不再变化。这是因为当释放时间超过100 s时，如图2所示，污染源强度已经衰减至初始强度的十分之一，若50步时机器人还未成功定位到污染源，说明机器人已经陷入了局部浓度较大区域，此时真实污染源处的浓度已经非常低，且还在进一步衰减。当释放时间达到200 s（搜索步数为100步）时，真实污染源处的浓度几乎为0。因此，若50步时机器人还没有成功定位，则100步时仍然不会定位到污染源，故成功率不再变化。

对周期型污染源来说，当搜索步数超过50 步时，成功率略微增加，由89%增加到了92%。虽然在定位过程中，机器人仍然可能陷入局部浓度较大区域，但此时污染源是周期变化的，某一时刻的局部浓度较大区域在下一时刻可能变为浓度较小区域，因而机器人仍然有机会离开该区域，进而定位到真实的污染源。因此当搜索步数超过50步时，成功率会略微增加，但增加的幅度非常有限，此时再增加搜索步数已经意义不大。通过本文研究，认为实际应用时，可以将机器人的最大搜索步数定为50步。

5 结论

本文将NM 算法与机器人主动嗅觉相结合，对室内衰减型和周期型两种时变污染源开展定位研究，主要结论如下：

（1）衰减型污染源由于呈指数型衰减，源强度衰减速率大，且在通风和障碍物的共同作用下会在真实污染源的左侧形成局部浓度较大区域。随着搜索时间的推移，该区域不断扩大左移并向四周扩散，且真实污染源处的浓度快速衰减，导致机器人非常容易陷入局部浓度较大区域，因而定位难度较大。

（2）周期型污染源虽然在通风和障碍物的共同作用下也容易形成局部浓度较大区域，但是该区域会随污染源周期性波动，且浓度最大区域始终位于真实污染源处。因此虽然机器人可能也会陷入局部浓度较大区域，但大都可以离开该区域并最终成功定位到污染源，故周期型污染源的定位难度要小于衰减型污染源。

（3）对机器人数量、响应时间和最大搜索步数这三个影响因素进行讨论，通过分析发现当机器人数量为5个，响应时间为2 s，最大搜索步数为50步时，定位效果最好，此时两种时变污染源的定位成功率均在80%以上。值得注意的是，本文的研究是基于普通的办公室、实验室等区域（12 m×8 m），故该结论适用于面积为100 m2左右的室内空间。然而，对于尺寸较大的室内空间，例如飞机场、高铁站等，仅依靠5 个机器人可能无法有效地对污染源进行定位，此时该结论的适用性需要进一步地探究。此外，本文机器人除考虑避障措施外，仅利用了浓度信息，若进一步搭载风速及风向传感器，利用风速风向等信息，则该结论可进一步优化。