基于一种标准城市建筑模型的行人高度风环境比较研究
杨 易,张之远,余先锋
(华南理工大学亚热带建筑科学国家重点实验室,广东 广州 510640)
高层建筑将影响正常风的走向,可能恶化其附近区域行人高度风环境的品质,给行人的舒适度和安全造成潜在不良影响[1]。随着我国城市的快速发展,数量日益增长的高层建筑对行人风环境的影响已不容忽视,成为值得关注的研究问题。
建筑周围行人风环境的研究手段主要有风洞试验和计算流体动力学(computational fluid dynamics,CFD)数值模拟[2]。张爱社等[3]利用数值模拟研究了某建筑群周围风的绕流特性,发现在某些风向角下建筑之间会产生复杂的漩涡脱落现象,并使建筑拐角处的风速明显增大,恶化局部行人风环境。Tsang等[4]用风洞试验研究了单体高层建筑的宽度与高度对周围行人风环境的影响,发现建筑迎风面尺寸变宽会恶化附近的行人风环境;而高度的增加会使下游区域的风速比变小。Iqbal等[5]对十字形截面的高层建筑群进行CFD模拟研究,结果表明不同风向角对建筑角区的回流和风速有显著影响。Tse 等[6]利用风洞试验研究了扭转风场中单体建筑周边的行人风环境,发现与常规风场相比,在建筑下游产生的低风速区域更大而高风速区域变得更小。Xu等[7]利用风洞试验研究了不同体型的超高层建筑周围的行人风环境,发现400 m 超高层建筑周围的最大风速比200 m更大。Tamura 等[8]采用风洞试验研究了方形截面建筑周围的行人风环境,发现建筑高度增加会导致最大加速比与高风速区域增加,而建筑宽度增加会加剧“文丘里”效应。Zhang 等[9]基于RANS(Reynolds-averaged Navier-Stokes)方法研究了各种非常规体型的超高层建筑对周围行人风环境的影响,发现超高层建筑会使周围区域的行人高度风速最大值增大1.5~2.5倍。谢壮宁等[10]利用风洞试验研究了单体高层建筑在不同风向角下的加速比和平均风速比等参数的变化规律,发现各风向角下的最大加速比都约为1.9,而行人风环境不适的区域出现在建筑背风面角隅处。
综上所述,围绕高层建筑附近行人风环境的研究已开展了不少工作,但对高层建筑高度与行人高度风速的加速程度之间的定量关系仍缺乏系统研究。本文以日本建筑学会(Architectural Institute of Japan,AIJ)提出的一类城市建筑风环境模型[11]为基础(该模型也被纳入近年新颁布的广东省《建筑风环境测试与评价标准》[12]),分别采用风洞试验以及RANS 和LES(large-eddy simulation)的数值模拟方法进行系统研究,以详细讨论不同高层建筑高度和来流风向角对中央建筑附近行人风环境的影响规律。
1 模型概况
AIJ提出的城市建筑行人风环境模型,其平面示意图如图1 所示,包括1 栋中央建筑和周边78 座低矮建筑。中央建筑的原型尺寸为25 m×25 m×h(h为建筑高度),周边建筑对应的原型尺寸为40 m×40 m×10 m。为研究中央建筑高度对行人风环境的影响,本研究设计了14 组不同高度的风洞试验模型,如表1 所示。考虑到模型的对称性,如文献[13]中的测点布置方案,本次试验在中央建筑周边行人高度处布置了33个测点,如图2所示。

图1 行人风环境风洞试验建筑模型平面图(单位:m)Fig.1 Plane view of building model for pedestrianlevel wind environment wind tunnel test(unit:m)

图2 行人风环境测点布置图Fig.2 Layout of measuring points for pedestrianlevel wind environment

表1 建筑风环境模型中央建筑高度Tab.1 Heights of central building in wind environment models
2 风洞试验
行人风环境风洞试验在华南理工大学大气边界层风洞中进行。试验模型缩尺比为1:300,风场为B类地貌,地面粗糙度指数α 为0.15,参考高度为300 m,在参考高度处测得的参考风速为11.3 m·s-1。风洞中模拟得到的顺风向平均风速剖面、顺风向湍流度剖面等风场参数如图3 所示,其中平均风速剖面与规范吻合较好,顺风向湍流度剖面有所偏差但仍可接受。行人高度风环境风速的测量采用实验室自制的改进欧文风速探头(图4),该探头降低了常规欧文探头的风向敏感性,同时提高了探头测试的可重复性、准确性与可靠性。探头安装高度为5 mm,相当于原型尺度1.5 m高度处。风洞试验风向角参考风环境规范[12]中取22.5°间隔进行了16 个风向角的全风向测试,其中0°、45°和90°风向角的方向如图5所示,试验中的模型如图6所示。

图3 风洞试验模拟的大气边界层风场特性Fig.3 Boundary layer wind field properties simulated by wind tunnel test

图4 行人风环境测量中的改进欧文风速探头Fig.4 Improved Irwin probes in pedestrian-level wind measurement

图5 风洞试验风向角示意图Fig.5 Wind incident angles in wind tunnel test

图6 建筑风环境风洞试验模型Fig.6 Building model for pedestrian-level wind environment
3 数值模拟
3.1 计算域与网格划分
为保证堵塞率小于3 %的要求,计算域的尺寸取为L×B×H=4 000 m×2 000 m×400 m(原型尺寸),计算域尺寸以及边界条件如图7 所示。采用内、外域分区网格划分方法,利用规则拓扑结构的六面体网格单元进行离散,使得网格排列方向与各风向角下的流动方向一致,从而提高计算效率并减小数值扩散误差。由于近壁面流场速度梯度较大,近壁面网格需进行加密。在数值风洞网格划分过程中,通过调整近壁面网格密度,采用三种连续变化的网格密度模型,进行数值模拟结果的网格无关性检验。其中基本网格模型将离地面第一层最小网格高度设置为0.4 m,网格垂直高度变化比率为1.06,近壁面y+值约为30~50。外域网格单元总数约为147 万,内域网格根据建筑高度的变化从293 万到433 万。另外两种网格模型分别将离地第一层网格高度设置为0.28、0.56 m,这样在2倍近壁面网格密度范围内进行网格无关性检验。中央建筑为100 m时模型的计算域网格划分如图8所示。

图7 计算域尺寸及边界条件(单位:m)Fig.7 Computational domain size and boundary conditions(unit:m)

图8 计算域网格划分Fig.8 Calculation domain mesh generation
3.2 湍流模型与边界条件
CFD数值模拟基于RANS和LES两种模拟方法,其中RANS方法和LES方法分别在ANSYS CFX 15.0和ANSYS Fluent 15.0上进行计算。钝体绕流CFD模拟中湍流模型将对结果的准确程度与可信度产生很大影响[14],故选择合适的湍流模型十分重要。在RANS模拟中,采用Menter[15]提出的对钝体结构分离流动具有较高精度的剪切应力输运(shear stress transport,SST)k-ω模型。入口边界条件的定义将极大影响边界层风场的自保持特性,为生成具有平衡态的大气边界层风场,在入口边界上采用Yang等[16]提出的一类指数律数学模型,如式(1)—(4)所示:
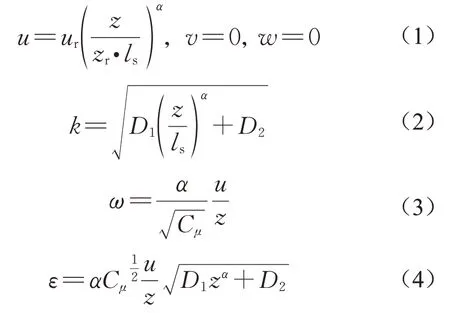
式(1)—(4)中:u、v、w分别为三个方向的风速;k为湍动能;ω和ε为湍动能耗散率;ur为参考风速11.3 m·s-1;z为离地高度;zr为参考高度300 m;ls为缩尺比1/300;α为地面粗糙度指数0.15;D1、D2根据在华南理工大学风洞试验中模拟的风场试验数据进行拟合。同时通过大量无建筑空风场中的自保持性模拟,选取湍流参数Cμ的取值为0.08。内层Wilcoxk-ω模型参数为[17]:α1=0.413,β1=0.033 3,σk1=1.176,σω1=2;外层k-ɛ 模型参数为:α2=0.20,β2=0.036 8,σk2=1.0,σω2=1.168。流动为三维不可压缩定常流动,速度-压力耦合方式为SIMPLEC,动量方程和湍流模型方程扩散项采用二阶迎风格式,对流项为QUICK 格式,所有变量和连续性方程残差收敛标准设为10-5。
采用LES模拟分为两步,先用RANS 中的SSTk-ω模型进行稳态计算,然后把计算结果作为初始化条件再用LES 进行瞬态计算。在采用LES 方法进行风工程绕流模拟时,准确模拟大气边界层湍流风场同样是保证计算结果准确性的前提,这也是当前计算风工程领域中的一个基础性难题与研究热点[18]。近年来关于此问题也有不少研究进展,如Huang 等[19]改进了Smirnov[20]的方法不满足大气边界层卡曼谱的不足,提出了离散合成随机湍流法(discretizing and synthesizing random flow generation,DSRFG);Aboshosha等[21]引入了调谐因子改进了空间相关性,提出了一致离散随机湍流法(consistent discrete random flow generation,CDRFG)方法;Yu等[22]从单点窄带过程叠加的角度出发提出了计算效率和精度更高的窄带合成随机湍流法(narrowband synthesis random flow generator,NSRFG)。
本文采用NSRFG 方法编写成用户自定义函数(user-defined function,UDF)生成入口湍流,再通过编译与FLUENT链接进行计算。速度-压力耦合方式采用压力隐式算子分割(pressure-implicit with splitting of operators,PISO)算法,时间离散选取采用二阶隐式格式,空间离散选取二阶中心格式,亚格子模型采用动态Smagorinsky-Lilly 模型。为了兼顾计算精度和时间成本,时间步长选为0.002 s,模拟总时长设为10 s,所有变量和连续性方程残差收敛标准设为10-4。RANS和LES模拟的边界条件和对应的数学模型如表2 所示。由于篇幅限制,中间结果未在文中一一展示。在作者团队已发表的文献中,均进行了自保持验证,例如RANS模拟中的自保持验证见文献[16]。

表2 数值模拟边界条件Tab.2 Boundary conditions for numerical simulation
4 结果与分析
为比较不同中央建筑高度和来流风向角对建筑附近行人高度风速场的影响,风洞试验结果和数值模拟结果以量纲一风速比R来表示,其定义为测点风速与参考风速之比,如式(5)所示:

式中:V为风洞试验探头或数值模拟中监测点处的平均风速;Vr为来流方向离地面1.5 m 高度(原型)处未受建筑影响的监测点处平均风速,而两者比值R反映了建筑结构对来流风速的放大效应。在风洞试验中,通过距离地面0.8 m 处皮托管测得的实验值换算成离地面0.005 m 处的风速得到Vr;在数值模拟中采用了类似方法。
4.1 结果比较
将风洞试验、RANS 和LES 模拟得到的各测点在不同中央建筑高度、不同来流风向角下的风速比R值进行比较。考虑篇幅,本文仅展示中央建筑高度为100 m在0°来流风向角时,风洞试验和数值模拟中得到的各测点风速比R值,如图9 所示,其中wind1~wind33 分别代表1~33 号测点。可以看出,风洞试验、RANS 和LES 方法得到的各测点风速比R值随测点变化的规律整体上基本一致,其中RANS方法的结果与风洞试验数据的误差平均值约为30%;而LES 方法的结果与风洞试验更为接近,各测点速度比误差平均值约为15 %。分析风洞试验与数值模拟之间的误差来源,一部分来自于CFD模拟的误差,一部分也来自于风洞试验本身的误差。由于试验中风速监测点贴近地面,而近地表区域的湍流十分复杂;风洞试验中无障碍物的风场模拟结果在地表附近与规范中定义的理想风场模型误差相对较大,这也是二者误差的来源。

图9 风洞试验和数值模拟得到的各测点风速比R值(中央建筑高度为100 m在0°来流风向角下)Fig.9 Wind speed ratios of measuring points by wind tunnel experiment and numerical simulation (at a central building height of 100 m and wind incident angle of 0°)
4.2 建筑高度的影响
为了直观比较建筑高度和来流风向角对高层建筑周边行人高度(1.5 m)风速分布的影响,将风洞试验和数值模拟得到的不同中央建筑高度下的风速比绘制成云图,如图10所示。图中仅展示来流风向角为0°,中央建筑高度分别为10、50、100、150和200 m时在中央建筑附近的风速场结果。
由图10可以看出:(1)在0°来流风向角下中央建筑高度连续变化时,RANS 和LES 模拟得到的各测点风速比分布规律整体上与风洞试验基本一致。(2)其中LES 结果与风洞试验结果更为接近,在建筑侧风面和背风面LES 模拟出了风速明显加速的区域;相对而言,RANS 模拟结果一定程度上低估了行人高度风速,表现在没有准确反映出建筑背风面的加速区域,且在中央建筑上侧面的高风速区也不明显。(3)RANS 计算结果未能很好再现复杂建筑群绕流产生的流动分离现象。

图10 不同中央建筑高度下风洞试验和数值模拟得到的行人高度风速比云图(0°来流风向角)Fig.10 Wind speed ratio cloud diagrams of central buildings with different heights obtained by wind tunnel test and numerical simulation (0°wind incident angle)
由风洞试验结果可以看出:(1)随着中央建筑高度的增加,建筑周边行人高度风速逐渐增大;当中央建筑高度达到100 m 时,局部风速比R值达到1.6,即局部区域风速相对来流风速增大约1.6倍。(2)随着建筑高度增加到150 m,R值与高风速区域略有增大;但建筑高度高于150 m 达到200 m 时,R值与高风速区均不再增加。由此得出,当中央建筑高度逐渐增大时,会使得建筑周围行人高度风速逐渐增大;但中央建筑高度超过一定高度后,将不再影响建筑底部行人高度的风速场(对于本文研究的案例,中央建筑高度的影响范围为周边建筑高度的10~15 倍左右)。
4.3 来流风向角的影响
除建筑高度,来流风向角也会影响高层建筑附近行人高度处的风速场分布。图11 列出了风洞试验得到的100 m高中央建筑在0°、22.5°、45°、67.5°和90°这5个典型来流风向角下的风速比云图。
由图11 可以看出:(1)当来流风向角在0°~90°范围变化,高风速区域总是出现在中央建筑背风和迎风角区,高风速比区域形状近似为扇形,与中央建筑背风区的漩涡脱落有关。(2)在来流风向角方向上,在紧邻中央高层建筑的通道里也出现高风速比区域,这是由于“文丘里效应”[23]导致,该效应指的是流体经过截面变小的通道时会发生加速的现象。(3)不同来流风向角会对高层建筑行人风环境造成不同程度的影响,当风向角为45°斜风来流时,加速情况相对最严重。因此在进行高层建筑行人风环境评估时,需要重点考察相对建筑方位为斜风来流的工况对周边行人风环境的影响。

图11 不同来流风向角下风洞试验得到的行人高度速度比云图(中央建筑高度为100 m)Fig.11 Speed ratio cloud diagrams of different wind incident angles obtained by wind tunnel test (at a central building height of 100 m)
5 结论
本文基于AIJ 提出的一类建筑群风环境模型,分别采用风洞试验和数值模拟方法,系统研究了不同工况下中央高层建筑周围行人高度风速场的分布规律,以探讨数值模拟结果和风洞试验结果的差异,以及不同中央高层建筑高度和来流风向角的影响。有如下主要结论:
(1)风洞试验、RANS和LES方法模拟得到各测点风速比变化趋势整体上一致,但RANS 与风洞试验结果之间的平均误差约为30%,而LES模拟误差相对更小,约为15%。RANS方法总体上低估了行人高度风速,没有准确反映出建筑背风面的加速区域;LES 模拟结果也验证了窄带合成随机湍流法(NSRFG)生成入口湍流在模拟复杂建筑群绕流风场的适用性和准确性。
(2)随着中央建筑高度的增加,建筑附近行人高度风速将逐渐增大。对本文研究案例,100 m及以上的超高层建筑对建筑底部局部区域行人高度风速场的加速将达到1.6倍,但当中央建筑高度超过150 m继续增大至200 m时,行人高度风速将不再增大。
(3)当风向角在0°~90°范围变化,在高层建筑背风和迎风角区发生流动分离处出现高风速区域;当来流风向角为45°斜风来流时,风速加速情况相对最严重,对行人风环境最不利。

