智慧课堂视角下数学直观想象能力的培养

连丽萍 刘 燕

(福建省福州华侨中学 350004)

直观想象是数学六大核心素养之一，是借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.直观想象能力是数学的一项基本的重要能力.诸多数学能力中，直观想象能力在生活中的运用较为广泛，且与物理、化学、美术等学科学习的关系较为密切.培养学生直观想象能力，为学生创造一个开放的文化氛围、一个较完善的教育环境，使教师把更多的注意力放在教学的最优化、资源的整合、培养学生主动学习研究、终生求知的能力上，促进学生提高自身素质.将二者结合在一起，有助于提升学生的数学直观想象能力，提升学生的数学核心素养.

在实际课堂教学中，教师们要借助智慧课堂，利用信息技术多种方式，有效地开展课堂教学活动，化抽象为具体，让学生在智慧的教学环境中，从图形获得感性的认识，从而培养学生直观想象能力.

1 几何画板在数学教学中的应用

例1(2021年福建省厦门市中考数学二检试卷)四边形ABCD是正方形，⊙O经过A，D两点且与BC边相切于点E，动点P在射线BC上且在点C的右侧，动点Q与点O位于射线BC的同侧，点M是BQ的中点，连接CM，PQ．

(1)如图1，若点M在⊙O上，且CE=CM．求证：CM是⊙O的切线；

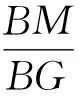
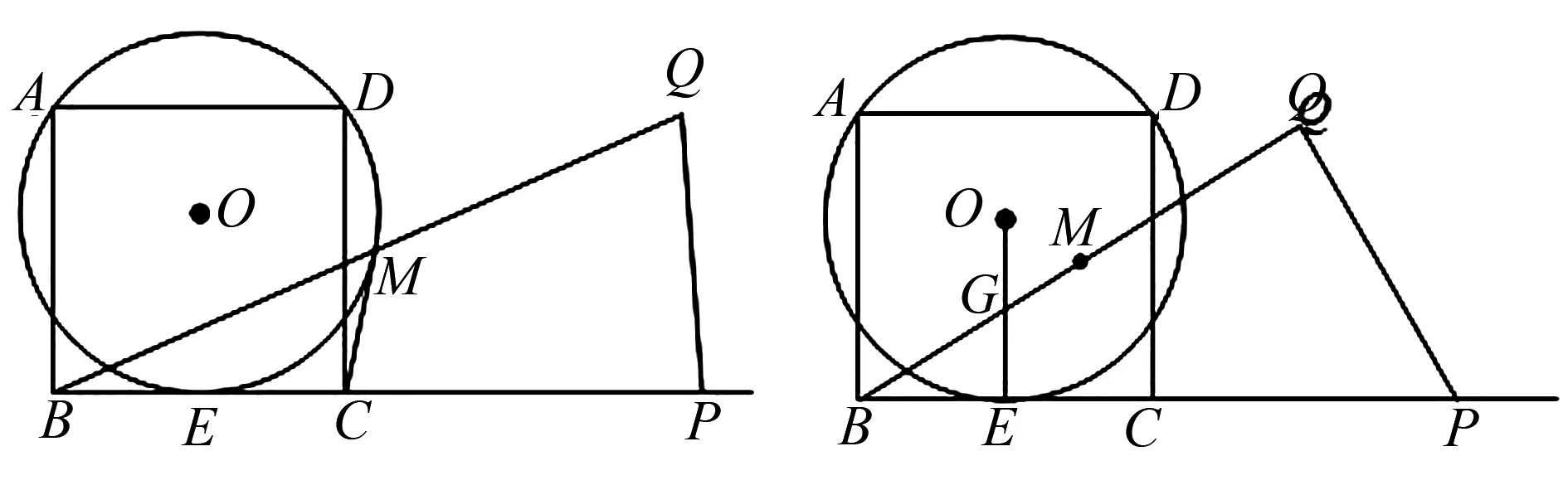
图1 图2

分析第(2)问要求直接写出m的取值范围，这“直接”却难倒不少学生.很明显，m的取值范围与点M有关，因此先要明确M的运动轨迹，不少同学以为M的运动轨迹是一段弧.这就需要我们先分析什么带动M的运动.在求解(1)、(2)问时，可得EM是△BCQ的中位线，又△CPQ为等边三角形，从而得到M的轨迹是过E点，且平行于直线CQ的直线在圆O内的部分.△CPQ的大小是由动点P在射线BC上的移动而变化的，因此是点P的变化引起了CQ的变化，从而引起了EM的变化，因此只要求出EM的取值范围，就能求出m的取值范围.原理都明确后，学生还是不太容易想到M的动态变化，这时候老师就可以借助几何画板向学生直观展示M的变化，化抽象为直观.

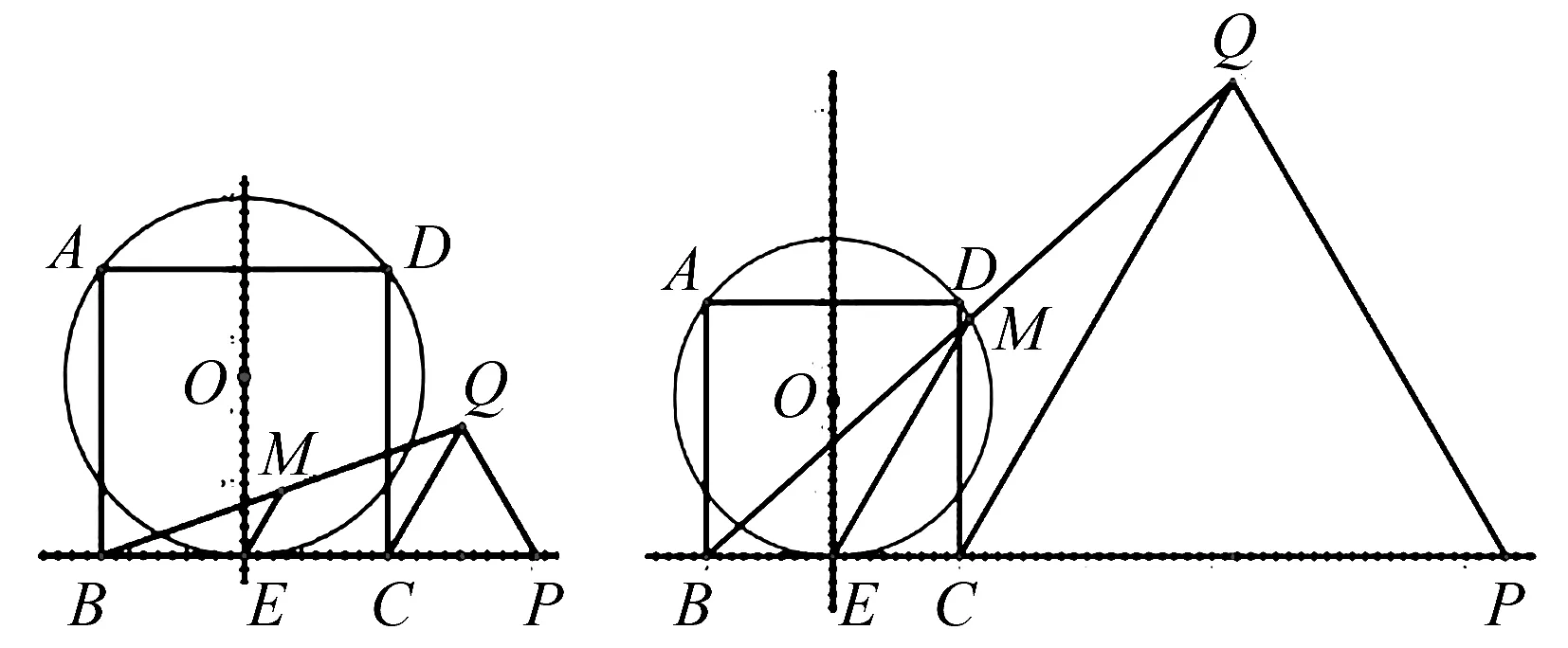
图3 图4

借助图形可以使问题的解决思路很快地显现出来，有利于揭示问题的本质.在进行复杂的逻辑推理或数学运算时，需要利用直观想象来梳理思路，寻找方向，将复杂问题简单化.

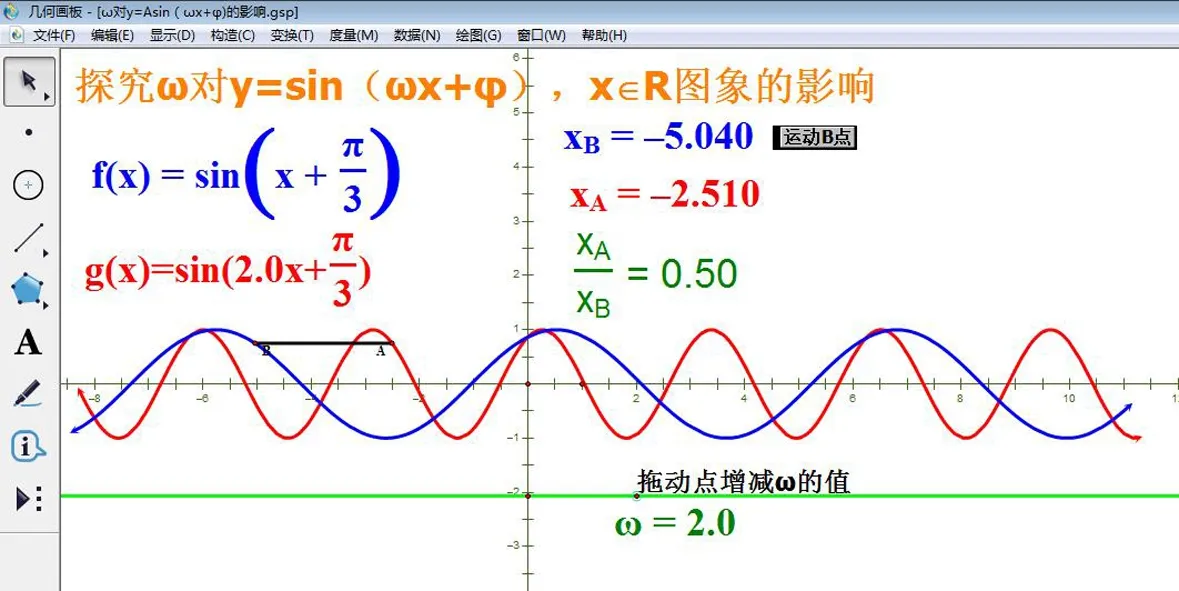
图5

例2学习《函数y=Asin(ωx+φ)的图象》这一课时，要研究函数y=sinx与y=Asin(ωx+φ)之间的图象变换关系，特别是ω对y=Asin(ωx+φ)的图象的影响，学生感觉比较抽象，而且改变参数的值，就要画出相应的图像，比较费时间.可以让学生自己动手操作几何画板软件，通过三角函数图象的各种动态变换的演示，学生通过观察图象，由抽象到具体，由模糊到清晰，发现规律，培养了学生的观察和思考能力，培养了数学直观想象能力.

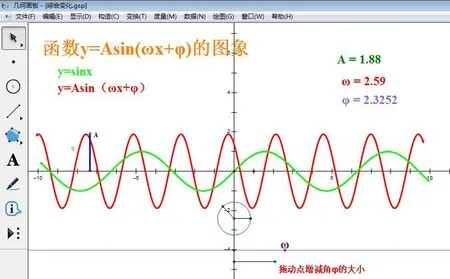
图6

我国著名数学家华罗庚对数与形的关系有如下生动的描述：“数缺形时少直观，形少数时难入微”，这道题借助几何画板，将数与形很好的融合，可以提高学生数形结合的能力.借助直观想象可以降低解决问题的门槛，使抽象的问题显性化、复杂的问题简单化.

2 希沃白板在数学教学中的应用

例3在学习长方体展开图时，虽然可以让学生通过拆开纸盒的方式获得长方体展开图，但发现学生几乎没有发现222型和33型的展开图，因此可以借助希沃白板动态演示这两种展开图，并且可以调节时间，让学生在较慢的演示过程中感受到原来还可以有这两种情形啊.从而培养了学生的空间想象能力.

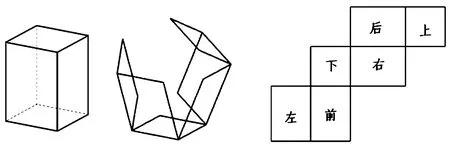
图7 图8 图9

3 投影仪、视频在数学教学中的应用

图10 图11

例4在学习黄金矩形时，要教学生折叠黄金矩形，学生照着书上的图片和文字，折叠有困难，特别是第三步：折出内侧矩形的对角线AB，并把AB折到下图中所示AD处.而教师在讲台上示范折纸，由于纸张不够大，坐在后排的同学不能清楚地看到老师的动作和纸的变化.这时就可以借助投影仪，把老师动作同步投影在屏幕上，或者老师事先录好折纸视频，调慢动作，学生通过观看视频，就能让书上抽象的文字和静态的图片直观动态地演示.

4 CAD在数学教学中的应用

例5某几何体的三视图均为如图所示的五个小正方形构成，则该几何体与其外接球的表面积之比为( ).

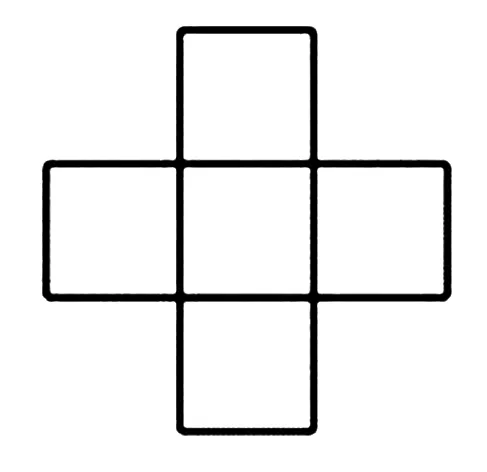
图12

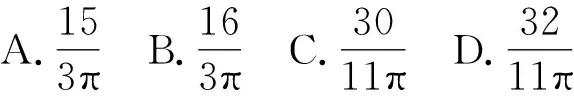
分析这题首先要根据几何体的三视图还原得到几何体，进一步求出几何体的表面积及外接球的半径，利用球的表面积公式，即可求解.可是难点就在于还原得到的几何体学生不好想象，教师不易用语言表达.这时可以借助CAD软件展示还原图，而且还能通过翻转几何体，让学生直观感知，从而培养学生的空间想象能力.

图13

例6新教材高一下学期必修二立体几何的课后习题，在透明塑料制成的长方体容器ABCD-A1B1C1D1内灌入一些水，固定容器底边BC于地面，再将容器倾斜.随着倾斜程度的不同，有下面几个命题哪些是真命题：____.

(1)有水的部分始终呈棱柱形；

(2)没有水的部分始终呈棱柱形；

(3)水面EFGH所在的四边形的面积为定值；

(4)棱A1D1始终与水面所在平面平行；

此类问题对学生的空间想象能力提出了很高的要求，解题过程大有“只可意会不可言传”的感觉，利用CAD软件我们可以动态多角度展示长方体的倾斜过程(如图)，让学生可以直观地感受在这个过程，水面的变化，从而对以上命题进行判断.利用CAD这个信息技术手段，可以很好地帮助学生培养直观想象能力，提升数学核心素养.

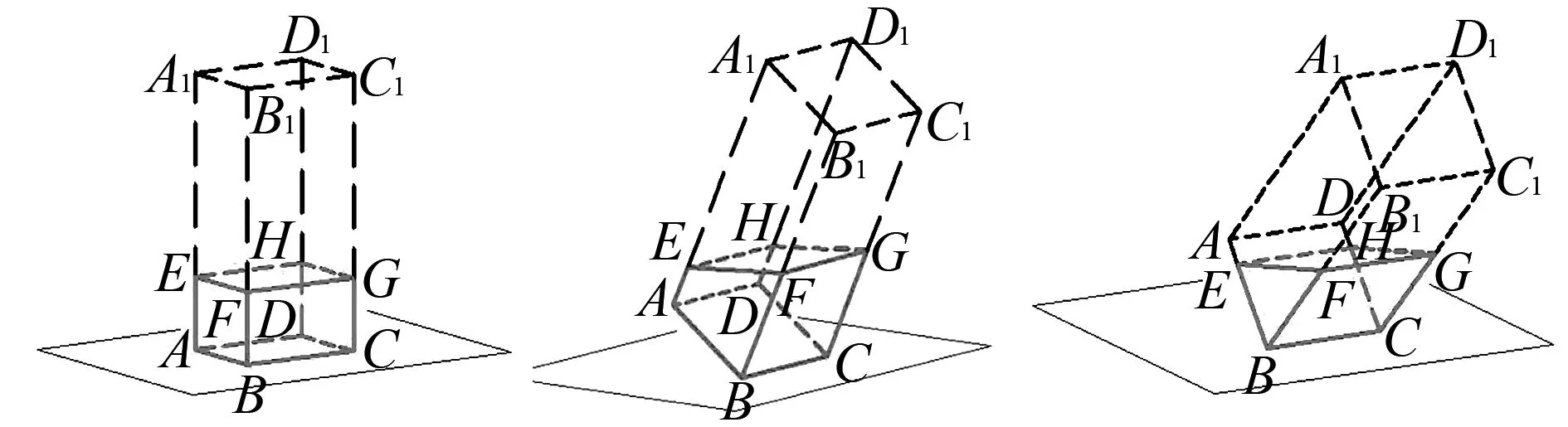
图14

5 GGB在数学教学中的应用

例7线面平行的性质定理

由于立体几何的结论很多采用直观感受的合情推理，并没有要求严格的推理论证的过程，因此在线面平行的性质定理中，想让学生按照课本所示，把严格的定理证明过程书写出来是相当有难度的.因此，在严格证明之前利用GGB软件辅助，如图先直观展示线面平行，当平面外直线a和该平面α平行，过该直线的平面β与原平面α有交线b，再通过旋转不同的角度，学生可以很直观地得到结论a∥b.利用信息技术可以提高上课效率，给学生的想象插上翅膀，为后续证明做好铺垫.

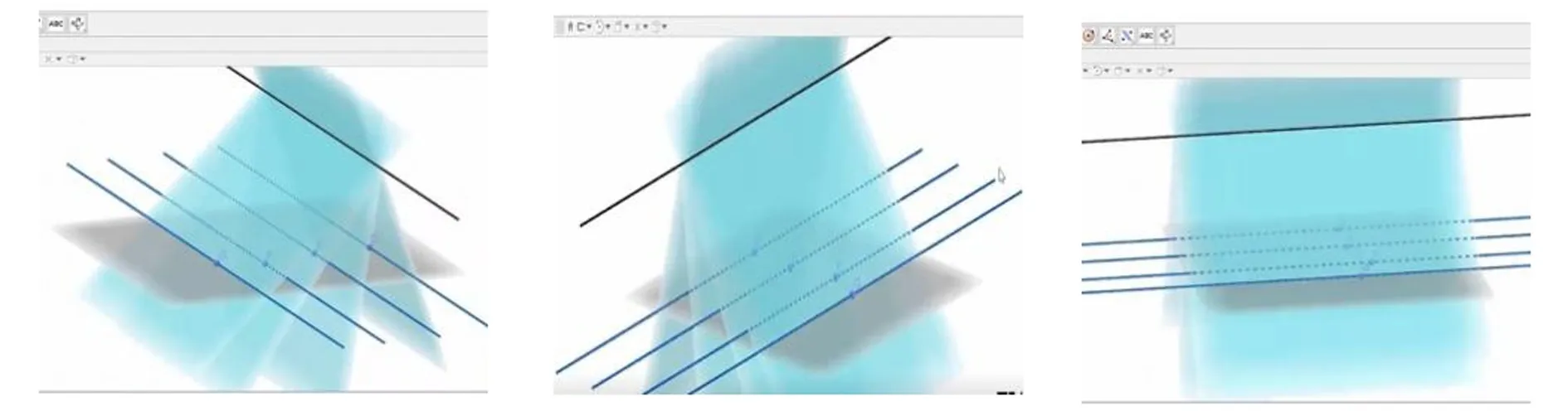
图15

在数学教学实践中，为培养学生的直观想象能力，提升学生的数学核心素养，一方面，教师应引导学生学好基础知识，深入理解数学概念、定理，并注重积累学习经验、解题技巧，另一方面，教师应做好教学工作总结，优选经典例题，通过借助信息技术手段，激活直观想象意识；引导操作实践活动，培养直观想象能力；借助直观作图解题，提升直观想象思维的策略，有效促进学生数学直观想象能力的提升.