函数思维在中学数学解题中的有效应用
孙高传
(江苏省南通市东方中学 226010)
中学生在进行数学解题时离不开解题思维的建立,而解题思维是学生在进行数学知识学习及内化时所形成的解题思路.一般来说,中学生在进行数学解题时所具备的解题思维包含抽象思维及函数思维等,但函数思维是中学生解题过程的核心,也是中学生学习时的重点及难点,其不仅可以加强各数学对象的联系,还可实现数学对象之间的转化,促进学生对数学本质变化的了解,提升学生数学解题能力,使其具备更加灵活及丰富的解题思路,促进其数学知识运用能力的提升.
1 关于函数思想
1.1 国内外的研究现状
解决数学问题的方法大家各显神通,但函数思想在国内外数学专家的眼中仍占据不可小觑的重要地位.数学家王太青曾说,中学教学过程中函数思想的运用十分重要.无独有偶,据国外学者们研究表明,函数作为一个备受数学家欢迎的概念,在教学实践中,对学生困惑的“变量”与“常量”的问题,引起大家学习的热潮.综上所述,在中学的数学教材中,函数的思维占据很大的比重,构建学生的函数思维体系,搭建数学整体的知识网络,是学生学习的重点.
1.2 国内教学大纲的要求
函数思想是数学思想中一种重要的思维方式,在教学中,也是一种重要的解题方式.在中学生学习函数的过程中,掌握函数相关的知识,可以帮助学生利用量变思维及函数思维分析问题,将数学问题进行巧妙的转化、归纳,利用逻辑,实现快速解题的目的.掌握函数的相关知识,可以指导学生将函数作为一种思维工具,更加多元、全面的应对数学难题,从函数性质作为切入点,构建函数的模型,分析是否能从函数的角度突破壁垒,顺利解决问题.
2 函数思维的特性
2.1 辩证性较强
函数思维隶属于辩证思维,具有较强的辩证性.在探讨各数学对象之间具备的联系以及其是否存在一定转化关系的过程中,加强对其辩证关系的了解,促进解题方法多样性建设,提升学生对数学的动态感知能力,培养学生的钻研精神,促进其解题能力的提高.
2.2 逻辑性较高
函数思维具有较高的逻辑性.相较于抽象思维而言,函数思维的逻辑性不仅强调其具有统一性及可调整性,还强调其应具有变化性,加强数与形的结合,推动二者关系的互相转化,促进代数与几何的联系性的提高,助推解题思路的拓宽.
2.3 变化性较多
函数思维具备的最基本特征就是变化性.函数思维具有一定的灵活性,可实现对各数学对象之间关系的反映,以函数的形式进行数学本质内涵的表达,提升其与数学发展的适应性,促进解题方法丰富性的研发.
3 函数思维在中学数学解题中的有效应用
3.1 函数思维在解方程题方面的应用
在解方程问题时,应以函数思维为指导促进已知关系与未知关系的转化,将函数性质作为解题的工具,加强函数的构造,将该方程问题转化为函数问题,促进解题方式的简化.
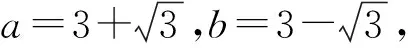
解析由已知条件可知a+b=6,ab=6,所以a、b为方程x2-6x+6=0的根.
当x=a时,a2-6a+6=0,2a2-12a+1=2(a2-6a+6)-11=-11
当x=b时,b2-6b+6=0,3b2-18b+1=3(b2-6b+6)-17=-17
由上可知(2a2-12a+1)(3b2-18b+1)=-11*(-17)=187.
3.2 函数思维在不等式解题方面的应用
在进行不等式解题时,通过对函数思维的利用,可加深学生对不等式意义及性质的了解,促进学生对不等式解题思路的掌握,提升其数学逻辑思维,加强图形与数学的结合,促进学生对问题深刻含义的理解,提高学生的函数构造能力.
例2x属于一些实数,而不等式|x+1|+|x-2|>m恒成立,求m的取值范围.
解析根据该题目可设f(x)=|x+1|+|x-2|,若f(x)=1-2x,则x≤-1,若f(x)=3,则-1 在进行不等式问题解答时,可有效借助函数思维,将图形与数学进行有机结合,促进对不等式问题的有效解答,实现数学思维的架构. 在进行二元一次函数解题时,可通过对函数性质的充分掌握,有效结合函数思维,促进解题技巧的提升. 例3 已知y与2x+1成正比例,当x=3时,y=10,求y与x的函数表达式. 很多数列问题的解题思路与函数思维息息相关,通过运用函数思维的分析思路,能帮助问题更加简化,提高做题的效率. 例4 已知的等差数列一共有10项,其中偶数项之和为40,奇数项之和为25,求公差. 解析此题可以将公差这个变量进行赋值,通过等差数列的定义,列方程组进行求解.设等差数列的首相为a1,公差为d,根据题目,可以得到两个方程式,分别是a1+a3+…+a9=25和a2+a4+…+a10=40,简化后的方程组为a1+4d=5和a1+5d=8,从而学生可以得出结果a1=-7,d=3. 在进行方程问题的解答时,将函数思维应用到其中,可有效促进问题解决程序的简化,降低学生对数学知识掌握的难度,加强函数与方程的联系,促进学生对相应问题思维导图的构建,提升学生知识的运用程度,使其主动投身入问题的解答中,促进自身数学思维的拓展.因此,教师应充分掌握每节课的教学内容,促进课程的合理化安排,提升函数与方程的联系,帮助学生架构合理的函数思维,引导其掌握构造函数的技巧,提高学生的想象力. 在进行数学不等式解题时,应加强对函数思维的利用,在掌握函数的定义域及值域等基础上,进行零点及极值的探索,促进不等式问题的解决.一方面,教师应加强对函数关系的明确,促进学生对未知关系的掌握.另一方面,教师在进行不等式解题时,可加强其与函数图像的联合,使学生对其具有一定的直观性,促进学生对解题条件的明确,使其充分了解题目的核心思想,提升将其转化为函数的效率,实现以函数思维进行问题解答的目标,促进解题步骤的减少,避免对学生解题思维的限制,提升学生图形与数学结合的能力,促进其学习水平的提高,从而充分展现相应的教学成果及成效. 二元函数具有较为复杂的性质及解题条件.为提升学生的解题效率,学生应提高自身的认知结构及认知水平,促进函数思维的升级.首先,教师应引导学生对二元函数表达形式的明确,加强对相应基础知识的掌握,如对称轴基本知识,图像基本知识以及交点式等,对繁多的知识点予以梳理,对学生进行逐步的灌输.其次,教师应促进二元函数复杂内容的简化.教师应具备丰富的专业知识,明确如何对学生加以引导,建立一定的切入点进行教导,如函数性质等,促进学生对知识结构的合理建设,使学生逐渐明晰教学内容. 传统的数学研究对象,一般分成两个部分,分别是数与形,虽然两者之间直观感受并无相通之处,其实不尽然.数与形的结合或者形与数的链接,是寻找问题解决方式的最佳切入点,提供给学生解决数学思路的双向路径,所以教师需要教导学生在应对数学题目以及解决函数问题的时候,最好的方法是数形并用,在了解题干的同时,简要画出图形,方便自己正确理解题目内容,高效绘制答案. 初中生的函数思维亦是如此,函数的定义概念勾勒出框架,而函数的性质展示函数的图像,两者之间缺一不可,教学过程中,培养学生数形的思维模式,借图修文,不仅可以提高学生学习的积极性,还能培养学生的逻辑思考能力. 很多学生或家长认为,函数思维只应用于当前阶段学生复杂的学习压力上,对解决生活中的实际问题毫无帮助,其实不然,学科的题目也偏生活化,将考试问题与函数思想联系起来,帮助学生建立场景,提高解题的效率. 总而言之,在进行数学教学时,不仅应注重学生对理论知识的掌握,更应注重学生对知识的应用,提高其知识应用的灵活性.教师应加强对函数思维的重视,并将其作为教学中的重点,促进教学方式的创新,加强学生函数思维的优化建设,促进教学质量的提升,还应加强对学生函数思维的训练,强化教学手段,在教学过程中加强函数思维的渗透,引导学生架构科学性的数学思维,促进其解题效率的提升,加强对学生探究式学习的培养,提升其解题水平.3.3 函数思维在二元函数解题方面的应用
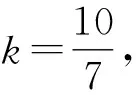
3.4 函数思维在数列解题方面的应用
4 在不同解题方面培养函数思维的教学策略
4.1 加强方程与函数之间的联系
4.2 促进不等式中函数关系的明确
4.3 加强对二元函数性质的掌握
4.4 与数形联系的解题思路
4.5 函数思维在生活中的应用

