阿贝尔判别法的推广

杜先云 任秋道

(1.四川省成都信息工程学院数学学院 610225;2.四川省绵阳师范学院数理学院 621000)

1 级数收敛的判定

目前《数学分析》与《高等数学》的教材中，给出了级数收敛与发散的定义，以及收敛级数的一些性质，判断正项级数收敛的比较多，而判断一般级数收敛的方法，只有柯西收敛原理，方法很少.本文给出二种判断一般级数收敛的方法，同时推广阿贝尔定理.

定理1 设{xn}为一个有界数列.∀ε>0，存在N∈Z+，当n>N时有 |xn-xn-1|<ε,则数列{xn}收敛.

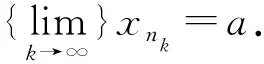
M=max{nk+1-nk|k=1,2,3,……}<∞.(1)

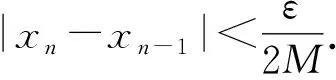
|xn-xnk0|=|xn-xn-1+xn-1-xn-2+…+xnk0+1-xnk0|≤|xn-xn-1|+|xn-1-xn-2|+…+|xnk0+1-xnk0|

于是，|xn-a|≤|xn-xnk0|+|xnk0-a|<ε.

根据数列收敛的定义，数列{xn}收敛.证毕.

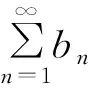
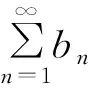
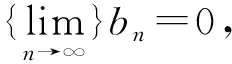
bn=xn-xn-1→0，(n→∞).

利用定理1可得结论.证毕.

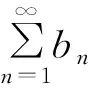
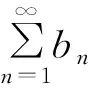
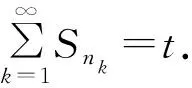
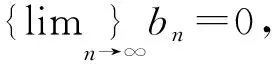
|Sn|=|Sn1+Sn2+…+Snk0+(bnk0+1+bnk0+2+…+bn)|

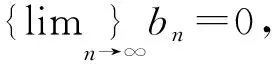
2 阿贝尔定理的推广

阿贝尔引理 设ai,bi(i=1,2,…,n)为两组实数.如果令σk=b1+b2+…+bk(k=1,2,…,n)，那么有部分和公式

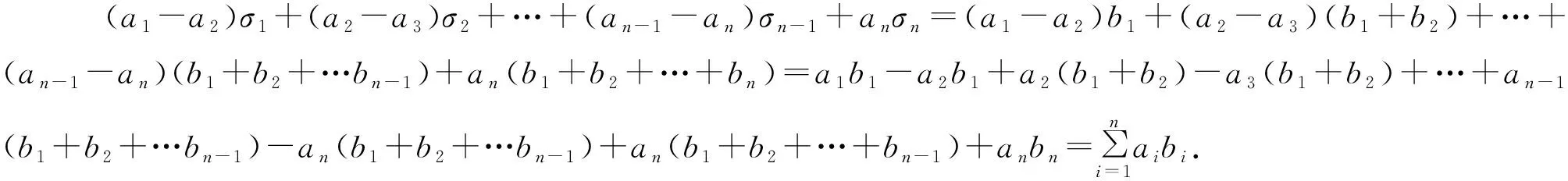
证毕.

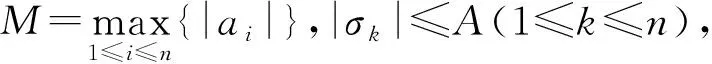
证明因为ai(i=1,2,…,n)为单调数组，不妨{ai}为单调递减数组，则有

ai-ai+1≥0，i=1,2,…,n-1.

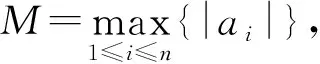
|a1-an|≤|a1|+|an|≤2M.

又因为|σk|≤A(1≤k≤n)，所以

≤(a1-a2)|σ1|+(a2-a3)|σ2|+…+(an-1-an)|σn-1|+|an||σn|

≤(a1-a2)A+(a2-a3)A+…+(an-1-an)A+|an|A

≤[(a1-a2)+(a2-a3)+…+(an-1-an)]A+MA

=(a1-an)A+MA

≤(|a1|+|an|)A+MA

=2MA+MA

=3MA.

对于{ai}为单调递增数组，结论类似，故结论成立.证毕.

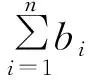
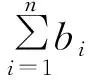
在数集{1,2,…,n}上作一一映射f，即f(i)=j(i=1,2,…,n)，并且相应地f(ai)=aj，f(bi)=bj(i=1,2,…,n)，使得f(a1),f(a2),…,f(an)单调.根据阿贝尔引理的公式(3)，可得

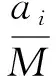
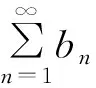
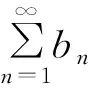
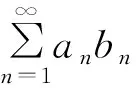
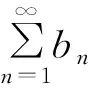
这是因为我们去掉级数前m项，不影响级数的敛散性.