反思解题再生习题资源，有效提升初中生数学解题能力

李晓玲

[摘  要] 数学学习不仅要重视解题，更要重视解题后的反思和回顾. 在教学过程中教师通过解题反思和总结的教学活动，培养学生自主学习和自主归纳的能力，让学生在独立思考、自主探究的过程中不仅知其然，更能知其所以然，体会解题思路和方法，有效提升解题能力.

[关键词] 解题反思;习题资源;解题能力

數学课程给人的传统印象是解题，注重解题的结果和结论的获得，而结论形成的过程却常常被忽略，以至于学生只记住了结论，不知道结论的由来过程，影响了学生学习能力的提升. 长此以往，造成部分学生习惯用记忆结论和模仿解题方法的方式进行学习，失去分析和探究问题的能力，不利于学生的长期学习和发展. 数学课程的教学不仅要关注解题结果，更要关注解题后的反思，处理好解题过程与结果之间的关系，才能真正激发学生的学习兴趣，让学生理解数学的本质和内涵. 笔者在教学中尝试从解题后的再认识和再创造，引导学生进行思考，探究试题的考查意图，总结解题方法，寻找解题规律，有效提升学生的解题能力.

案例  如图1，在△ABC中，∠B为直角，AB上有一点M，并且AM与BC相等，BC上有一点N，并且CN与BM相等，AN与CM相交于点P，求∠APM的度数是多少？

通过测量或者观察分析可以猜想出结论：∠APM=45°.

解法1  如图2，过点M向△ABC外作MD平行于CN，并截取MD与CN相等，连接DN与AD，因为四边形CMDN是平行四边形，所以DN与MC相等且平行，∠2与∠3相等. 又因为∠B为直角，MD平行于CN，所以MD与AB垂直. 因为CN与BM相等，MD与CN相等，所以BM与MD相等. 又因为AM与BC相等，所以△AMD与△CBM全等，所以AD，MC，DN相等，∠1，∠2与∠3相等，又因为∠1与∠ADM的和为90°，所以∠3与∠ADM的和为90°，即∠ADN为直角，所以△AND为等腰直角三角形，∠AND为45°. 因为DN与MC平行，所以∠APM与∠AND相等为45°.

那么这道题是否还可以利用图形变换的知识，寻找更多的解法呢？

反思考查意图，寻找多种解法

通过这样的解题方法，引导学生反思试题的考查意图、考查的知识点和数学思想以及构成的条件与试题背景之间的关系，找到考查的核心数学模型是等腰直角三角形. 通过观察和分析，添加了辅助线将AM与BC相等，CN与BM相等，进行有效利用，通过转换和平移的方式，构造出新的图形即平行四边形以及全等三角形，就可以得到等腰直角三角形. 通过解题后的反思，学生发现了一种全新的解题方法.

思路一：利用等量转换

通过图形的平移将相等的角或者线段进行等量转换，将已知条件与求证问题之间构建起联系，从而寻找解题思路. 本题就是将所求的角转换到一个等腰直角三角形当中，从而求得角的度数.

解法2  如图3，过点A作AD与BC平行，取AD与CN相等，连接CD和MD构造出平行四边形ADCN，并且出现全等△MAD和△CBM，从而得到等腰直角三角形DMC，可以得出∠APM与∠DCM相等为45°.

在反思中交流，进行归纳总结

解题结果的完成并不是真正完成了解题过程，解题之后还需要组织学生进行相互交流，将自己分析的思路和解题方法进行表达，生生之间互相倾听解题分析，将各种解题方法进行对比、分析和评价，互相取长补短，实现优势互补. 这样可以使学生加深解题过程的印象，也能培养学生的表达能力和合作能力，促进学生共同进步，协调发展.

思路二：利用图形的位置变化

图形可以通过平移、旋转等方式改变位置，但是不改变形状，从而实现有关角或者线段位置的变化，实现已知条件与所求结论之间的联系，进而找到解题的方法和策略. 本题中，为了构建所求的角与已知条件之间的关系，可以通过图形的旋转变化进行新的图形构造.

解法3  如图4，△ABC以点C为中心进行旋转，将CB进行顺时针90°旋转到CD，连接AD和DN，由此可以得到CD，CB与AM相等，CD与AB平行，这样可以构造出平行四边形CDAM和全等三角形，△DCN与△CBM全等，从而得到等腰直角三角形DAN，由此可以得出∠APM与∠DAN相等为45°.

通过上述几种解题方法的探讨可以看到，这些解法都需要用到“添加辅助线构造图形”的方法，这种“特别”的解法都围绕着角和线段的等量变换进行展开，运用到图形变化的多种方式，如平移、旋转、翻折等，通过改变图形的位置，在求答问题与已知条件之间构建联系，使结论与条件之间的关系充分显现出来，从而获得解题思路. 这样的变化是解题过程中常用的技巧，需要学生能够熟练掌握并强化，需要教师通过多种方式不断训练学生，使学生能够非常熟练地掌握这一解题的策略.

在解题之后反思解法，总结

成败经验

解题之后我们还常常需要反思刚刚的解题方法是否是最优解法，有没有更好的解法，解题方法是否需要进行改进等. 在进行复杂题型的解答时，我们并不能一开始就找到最佳的解法，因此需要在解题过程中不断地调整，以求找到最佳的解题路径. 因此在解题之后进行回顾，寻找最优解法，从而思考是否抓住问题的关键，反思解题过程，拓展学生思维，锻炼学生思维的灵活性和发散性，培养学生创新意识.

经过上述方法进行思考，学生又发现了另外一种解题方法.

解法4  如图5，过点A作AF与AB垂直，过点M作EM与AB垂直，过点C作FC与BC垂直，三条线的交点分别有点F和点E，由此得到矩形ABCF和正方形AMEF，再在CF上截取CG与CB相等，连接GN和GA，得到全等△GCN和△AFG，以及平行四边形AMCG. 这一解题方法与解法3的方法类似.

由此可以得到等腰直角三角形GAN，得出∠APM与∠GAN相等为45°.

这一解题方法较为烦琐，需要构造全等三角形和平行四边形，但是图形中由于有两个正方形，因此给了我们一些启示，那就是正方形的对角线可以平分对角得到45°，从而使得解法4能够找到另外一條解题思路. 通过相似三角形的对应角相等，再进行相应的转化就可以找到解题的结论，得到解法5.

思路三：利用相似图形进行变化

图形的相似变换需要利用数学性质或者概念中有关角或者线段进行位置转化，实现等量转换，从而在求答问题与已知条件构建联系，进而寻找解题思路.

解法5  如图6，过点M作EM与AB垂直，过点C作EC与BC垂直，交点为点E，连接AE和EN. 因为四边形MBCE是矩形，所以EC，BM相等，EM，BC相等，又因为AM与BC相等，BM与CN相等，所以△AME和△NCE是等腰直角三角形. 这样可以得到两个底角∠AEM和∠CEN都等于45°. 所以EM与AE的比值与EC和EN的比值相等，都等于. 又因为∠AEN等于∠AEM与∠MEN的和即∠CEN与∠MEN的和为90°，则∠AEN与∠MEC相等. 所以△AEN与△MEC相似，∠1与∠2相等. 因为∠3与∠4相等，所以∠AEM与∠APM相等为45°.

在反思中进行拓展延伸，总结规律

经过解法5的尝试，我们可以联想到其中经常使用到的一种解题方法，即两个正多边形如果共顶点，那么其对应顶点的连线的夹角正好等于其内角. 因为两个正多边形的边若相等，那么这两个正多边形相似，其对应的顶点连线的夹角就等于其共顶点的角.

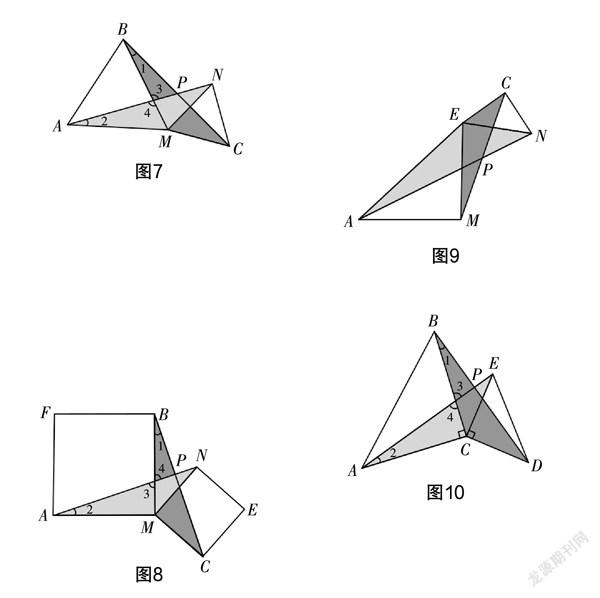
如图7，正△ABM和正△CNM，连接BC与AN相交于点P，那么可以得到∠APB为60°.

如图8，正方形AMBF和正方形CENM，连接CB和AN相交于点P，可以得到直角∠APB. 观察图8，可以证明△BMC和△AMN为相似三角形或者全等三角形，得到对应的∠1与∠2相等. 又因为∠3与∠4相等，所以∠APB与∠AMB相等.

因此可以进一步探究：两个等腰直角三角形共顶点，那么这两个等腰直角三角形相似吗？如图9和图10，可以发现其对应顶点的连线夹角也等于共顶点的角.

观察图9，等腰直角△AME和等腰直角△NCE相似，可以得到AE与EN的比值与ME和CE的比值相等，由∠AEM与∠NEC相等，可以得到∠AEN与∠MEC相等. 所以△AEN与△MEC相似，∠1与∠2相等. 因为∠3与∠4相等，所以∠APM与∠AEM相等为45°.

运用同样的解题方法可以得到图10中∠APB，∠ACB为直角.

由此可以得到进一步的猜想：两个三角形相似，其中有一对对应顶点为共点，那么另外两组对应顶点的连线的夹角与共顶点的对应角度数相等.

……

综上所述，解题之后反思试题本质，将题目的条件进行变化和联想，在图形变化中通过多种解法的运用，能锻炼学生的思维能力. 习题的反思和图形的变化，不仅在于探讨多种解法，更重要的是通过不同解法的探究，发展学生思维的灵活性. 通过解题反思，进行解题方法共性总结，可以总结规律，归纳解题方法，由特殊到一般，使学生的思维更加广阔，在探索中感受数学的魅力.