求解RLW方程的能量守恒有限差分格式

刘佳垚,王晓峰,钟瑞华

（闽南师范大学数学与统计学院,福建 漳州 363000）

在1966年，Peregrine[1]首次提出了一类非线性演化方程即正则长波（RLW）方程,在非线性色散介质的长波研究中,该方程可描述大量的物理现象,且它所描述的运动可以与KdV方程有相同的逼近阶,能够很好地模拟KdV 方程的几乎所有应用,因此对RLW 方程的研究无论在理论上还是在应用上都有非常重要的价值.有许多求解RLW 方程常用的数值方法,如有限差分法[2]、重心插值配点法[3]、拟谱法[4]和有限元方法[5]等.余跃玉等[6]通过对RLW方程的非线性项的线性化处理给出了一种新的线性有限差分格式.孙建安等[7]利用紧致有限差分和龙格库塔方法对RLW 方程在空间和时间进行离散,从而解决了对空间与时间混合导数的离散问题.陈佳欣等[8]对广义的RLW 方程初边值问题提出了两层线性守恒差分格式和三层非线性守恒差分格式.

考虑如下RLW方程的初边值问题

其中μ,γ为正常数,φ(0)=φ(L)=0.由能量方法可得得到式(1～3)满足如下守恒律

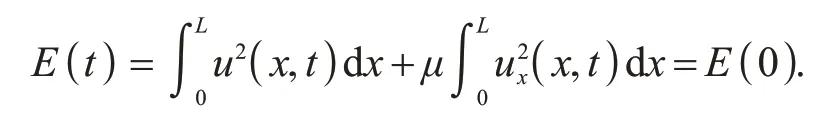
本文对式(1～3)构造线性Crank-Nicolson 外推型格式,在时间和空间上均达到二阶精度,构造的差分格式的系数矩阵是三对角矩阵,同时利用离散能量法证明了格式的收敛性、解的唯一可解性和守恒性,同时用数值实验的结果验证了理论分析的可靠性和有效性.

1 差分格式的构造

将区域[xL,xR]×[0,T]作网格剖分,令空间步长h=(xR-xL)/J,时间步长τ=T/N,其中J,N为正整数,记xj=xL+jh(0≤j≤J),tn=nτ(0≤n≤N).设≈u(xj,tn)为数值解,记

对任意的un,vn∈Z0h,定义如下符号：

对式(1～3)考虑如下差分格式：

其中

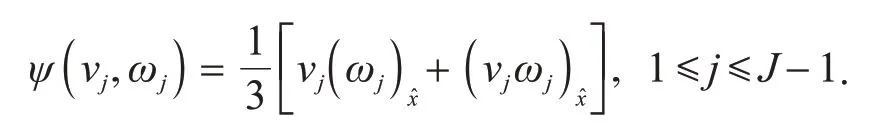
由于式(4)是一个三层差分格式,采用如下两层格式来计算u1

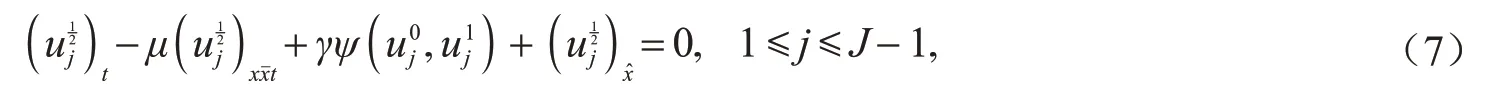
2 差分格式的守恒性

引理1[9]对任意的un,vn∈Z0h,则有

当un=vn时，有

引理2[9]对任意的un∈Z0h,则有

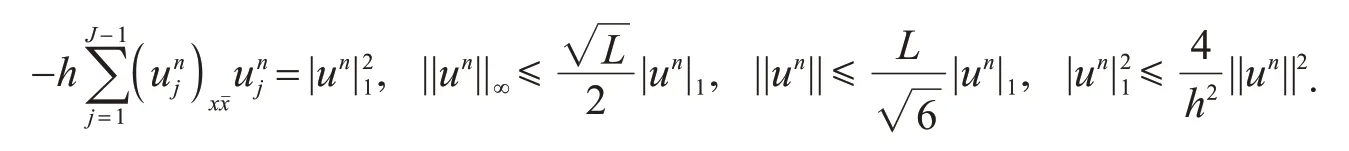
引理3[9]对任意的un,vn∈Z0h,则有

定理1设u0∈H20[xL,xR],u(x,t) ∈[xL,xR],则式(4～6)是满足能量守恒的,即

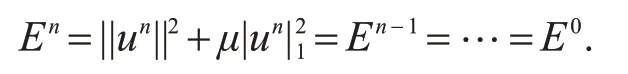
证明将式(4)与作内积得

由引理1和引理3得

整理式(8)可得

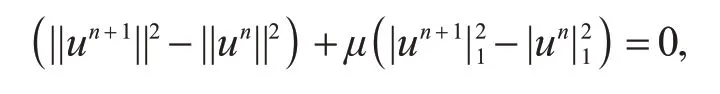
即

由En的定义,由式(9)的n递推可得En=En-1=…=E0.

3 差分格式的唯一可解性

定理2式(4～6)是唯一可解的.

证明用数学归纳法来证明,因u0由式(5)确定,由式(7)可计算u1,则u0和u1是唯一确定的.设u0,u1,…,un(n≤N-1)是唯一可解,考虑关于un+1的齐次线性方程组

将式(10)与un+1作内积,又由引理1和引理3可得

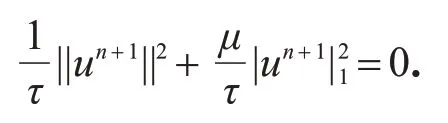
又由引理2得

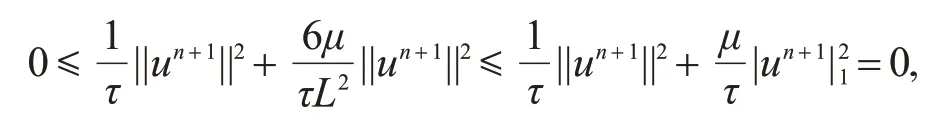
因而||un+1||=0,故差分格式(4～6)是唯一可解的.

4 差分格式解的收敛性

引理4[9]（离散的Gronwall等式）假设{Gn/n≥0}是非负数列,且满足

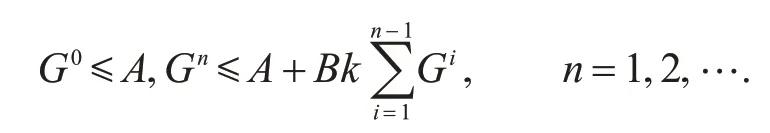
其中A和B均为非负数,则Gn=AeBnk,n=0,1,2,….

引理5[9]对任意的un∈Z0h,有如下关系成立

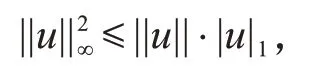
对任意的ε＞0,有

定理3设{unj|0≤j≤J-1,0≤n≤N}是差分格式(4～6)的解,是问题(1～3)的解,

令enj=U jn-unj,则存在常数C,使得

其中正常数C不依赖于τ和h,且在不同位置有不同的取值.

证明式(4～6)的截断误差为

同时有

将式(13～14)代入(12)中,可得

令Gn=||en||2+μ|en|21,则式(15)可写成

将式(16)中的n替换为l,并将式l=1到l=n求和可得

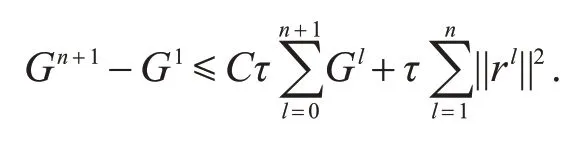
对于τ足够小,即有

其中

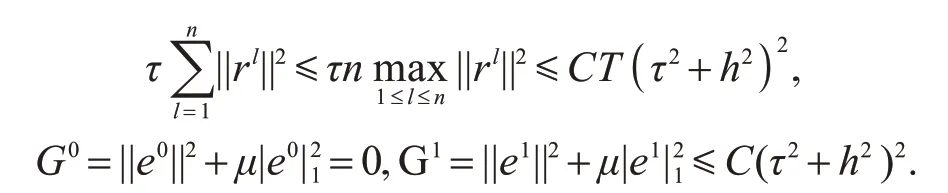
由离散Gronwall 不等式得Gn+1≤C(τ2+h2)2,从而||en||≤C(τ2+h2),|en|1≤C(τ2+h2).最后由引理5 可得||en||∞≤C(τ2+h2).

5 数值实验

为验证三层外推型结构式(4～6)的稳定性和守恒性,选取以下模型问题：

初始条件为

u0(x)=Asech2(kx+δ)，

已知方程的精确解[6]为

u(x)=Asech2(kx-ωt+δ)，

其中

设

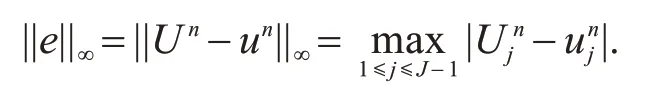
其中U nj=u(xj,tn)为精确解,unj为式(4～6)的解.定义空间和时间的收敛阶为

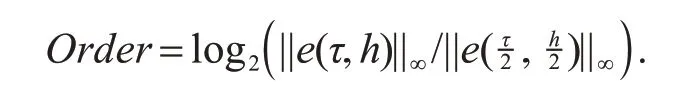
取xL=-30,xR=40,T=10,h=0.5,τ=h对式(4～6)进行计算,不同时刻的数值解和数值解的3D 图像见图1.分别取τ=h=0.5,h=τ=0.25,h=τ=0.125 和h=τ=0.0625 在同一时刻里不同步长下的误差和格式精度的计算结果见表1,从表1中可以看到所建格式收敛阶为二阶.分别取τ=h=0.5,h=τ=0.25和h=τ=0.125时能量守恒量的数值模拟见表2.

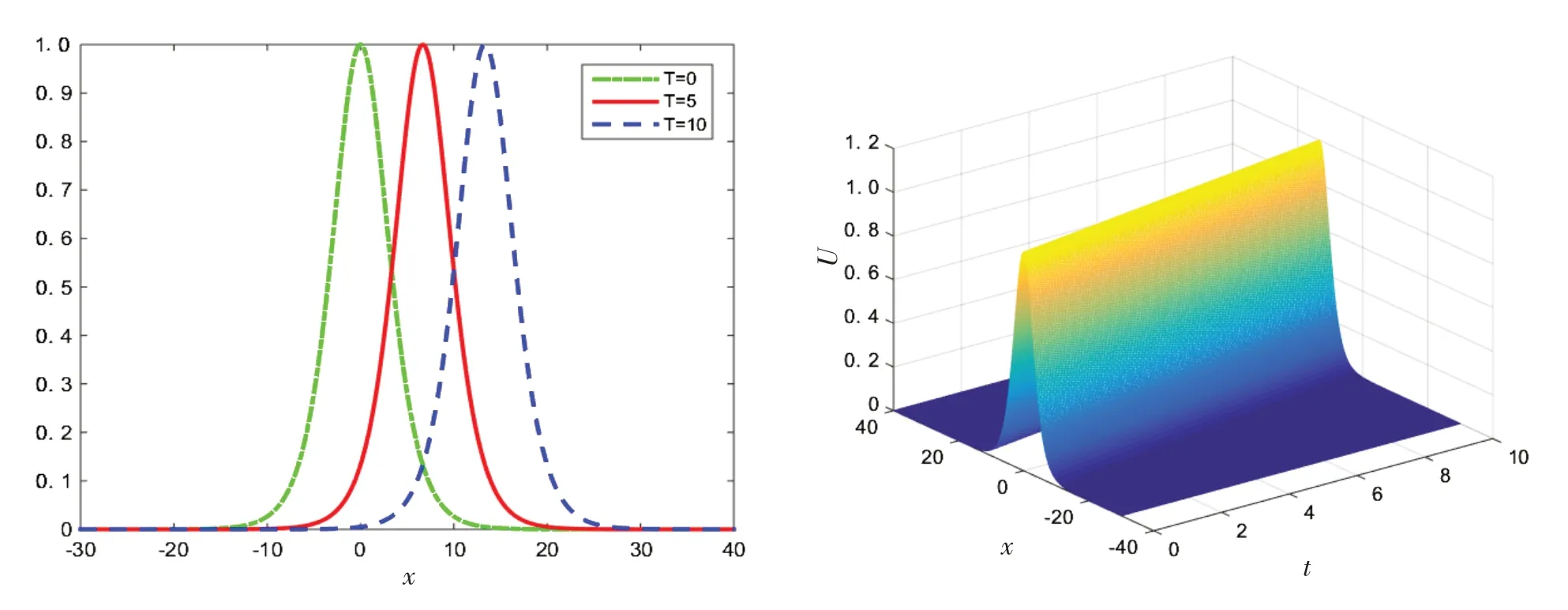
图1 不同时刻的数值解(左)和数值解的3D图像(右)Fig.1 3D image of exact solution and numerical solution(left)and numerical solution(right).

表1 在T=10下不同步长下的误差和格式精度Tab.1 Error and convergence at T=10 with different step sizes.

从表2可以看出，所建立差分格式保持了很好的能量守恒性.

表2 不同步长下的守恒量的数值模拟Tab.2 Numerical simulation of conserved quantity under different steps