关于商高数的Jeśmanowicz猜想*

管训贵

泰州学院数理学院，江苏 泰州 225300

设N*，N 是全体正整数和非负整数的集合，a，b，c为互素的正整数满足a2+b2=c2. 若2|b，则a，b，c可表成

这里u，v∈N*，u＞v，gcd(u，v) = 1，2| (u+v).

1956年，Jeśmanowicz［1］曾猜测：对任意n∈N*，丢番图方程

仅有解x=y=z= 2. 这是至今远未解决的数论难题。目前的结果大多集中在n= 1 的情形，而对于n＞1，只有为数不多的情形被解决［2-14］。其中一类典型的丢番图方程是a= 2k+ 1（k∈N*），c=b+ 1的情形。此时

1998 年，邓谋杰等［3］在假定a是素数方幂的前提下研究了这类情形，并证明了当(a，b，c) =(3，4，5)，(5，12，13)，(7，24，25)，(9，40，41)和(11，60，61)，即式（2）中k= 1，2，3，4，5时，方程（1）仅有解x=y=z= 2.

1999年，邓谋杰［4］又证明了当(a，b，c) =(13，84，85)，即式（2）中k= 6时，方程（1）仅有解x=y=z= 2.

2021 年，管 训 贵[6]证 明 了 当(a，b，c) =(19，180，181)，即 式（2）中k= 9 时，方 程（1）仅 有 解x=y=z= 2.

（i）z≡y≡0(mod 2)；

（ii）(c|p) =(e|p) = -1，f的某一素因子的方幂为奇数，或(c|p) =(f|p) = -1，e的某一素因子的方幂为奇数；

（iii）L=m2（m∈N*），z≡0(mod 2)；

（iv）L=m3（m∈N*），p≡2(mod 3)，z≡0(mod 3)；

（v）x≡y≡0(mod 2)，c=ξ2+η2（ξ，η∈N*，gcd(ξ，η) = 1，2|ξ），e(f)中某一素因子Q的方幂大于ξ(η)中Q的方幂，或pf(pe)中不含η(ξ)的某一个素因子。

于是在条件（i）～（v）之一成立的情况下，对任意n∈N*，方程（1）仅有解x=y=z= 2.

推论1当式（2）中k= 8，11，12，13，14时，方程（1）仅有解x=y=z= 2.

1 几个引理

2 定理1的证明

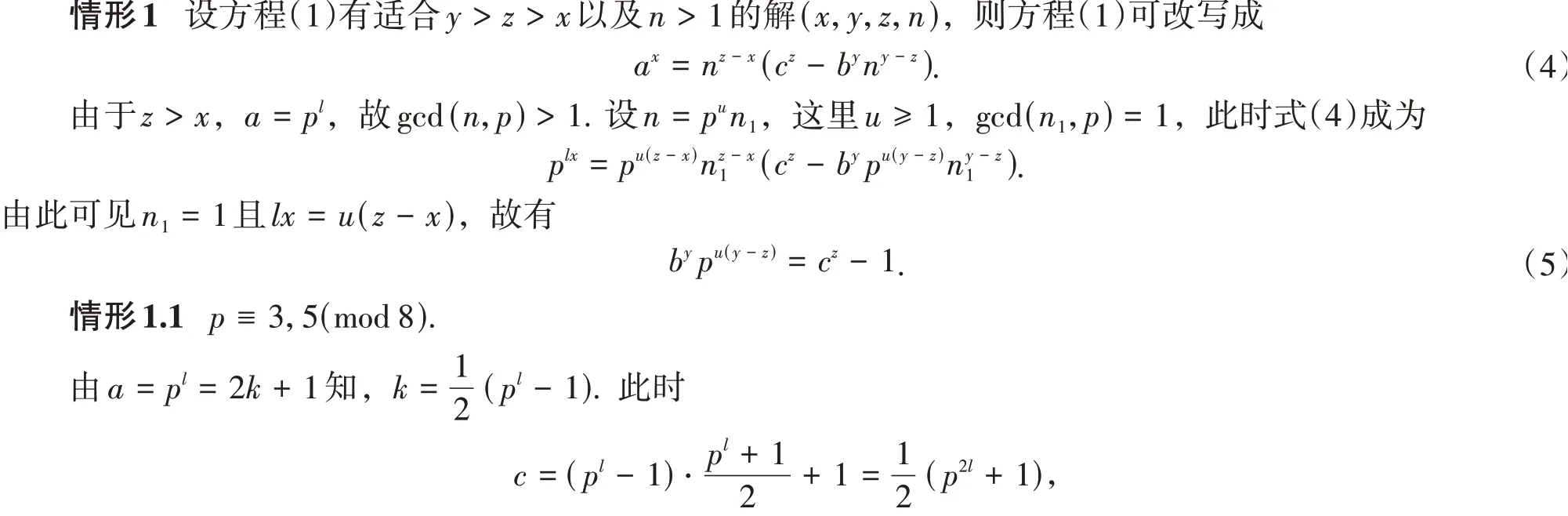
这产生矛盾，因此式（12）不成立。

情形2.2(c|p) =(e|p) = -1，f的某一素因子的方幂为奇数；或(c|p) =(f|p) = -1，e的某一素因子的方幂为奇数。

此 时 对 式（12）取 模p知， (c|p)z=(L|p)y， 即(-1)z=(-1)y， 这 说 明z，y同 奇 同 偶。 假 定z≡y≡1(mod 2)， 则 对 任 意i（i=k+ 1，…，l）， 由riy=si(z-y) 知2|ri， 与 条 件（v）矛 盾， 故z≡y≡0(mod 2). 再由条件（iv）知，式（12）不成立。

情形2.3L=m2（m∈N*），z≡0(mod 2).

此时可令z= 2z1，则式（12）成为

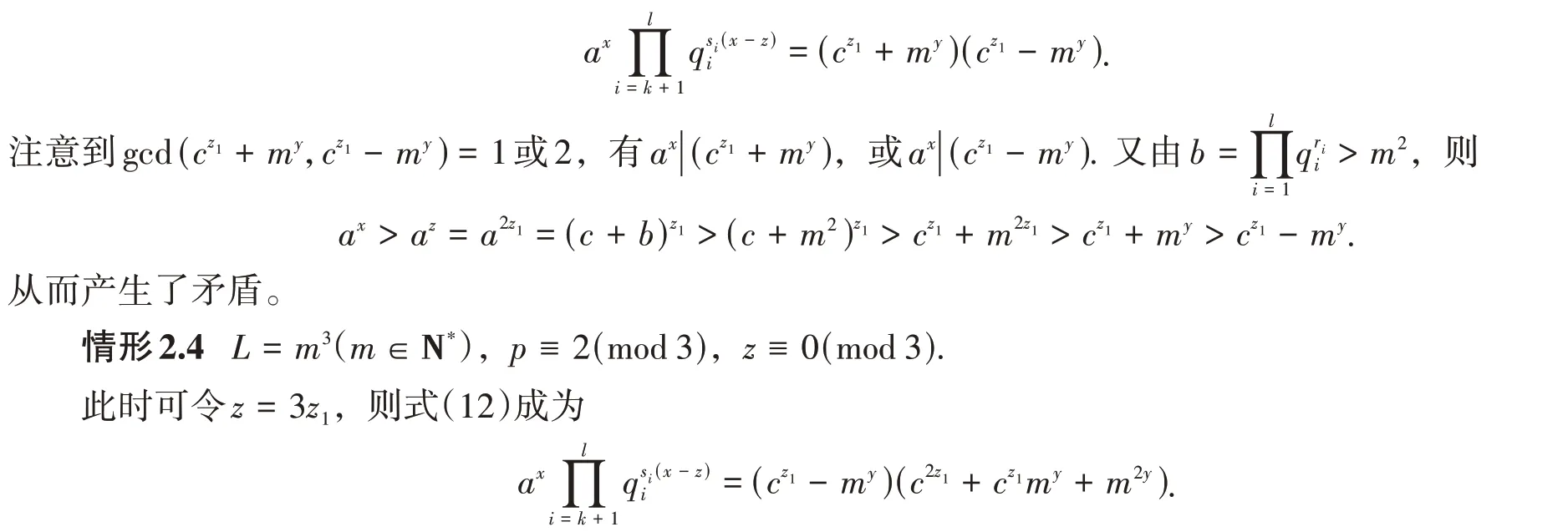
注意到gcd(cz1-my，c2z1+cz1my+m2y)= 1或3，有ax|(cz1-my)，或ax|(c2z1+cz1my+m2y).

若ax|(cz1-my)，则由情形2.2的讨论知这是不可能的。

若ax|(c2z1+cz1my+m2y)，则(2cz1+my)2≡-3m2y(modp)，由Legendre符号的性质得

矛盾。

情形2.5x≡y≡0(mod 2)，c=ξ2+η2（ξ，η∈N*，gcd(ξ，η) = 1，2|ξ），e(f)中某一素因子Q的方幂大于ξ(η)中Q的方幂，或pf(pe)中不含η(ξ)的某一个素因子。

当L=e时，假定z≡1(mod 2)，则由riy=si(z-y)（i=k+1，…，l）知，si≡0(mod 2)（i=k+ 1，…，l）.令x= 2x1，si= 2ti（i=k+ 1，…，l），y= 2y1，则式（12）成为

完全类似式（13）的讨论知，若f中素因子Q的方幂大于η中Q的方幂，或pe中不含ξ的某一个素因子，则式（16）不成立。于是z≡0(mod 2)，得z≡y≡0(mod 2). 再由条件（iv）知，式（12）不成立。

综上，在定理1 的条件下，方程（1）没有适合x＞z＞y以及n＞1 的解(x，y，z，n). 结合情形1、情形2、引理1、引理2和引理3可知，在定理1的条件下，方程（1）仅有解x=y=z= 2. 定理1得证。

3 推论1的证明

（A） 当k= 8时，(a，b，c) =(17，144，145). 此时方程（1）成为

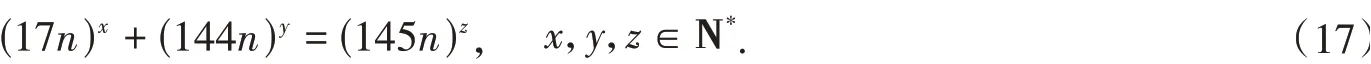
易知，方程（17）没有适合y＞z＞x以及n＞1 的解(x，y，z，n). 设方程（17）有适合x＞z＞y以及n＞1 的解(x，y，z，n). 由于b= 24· 32，故n= 2r3s（r，s∈N*，r+s≥1），于是方程（17）可化为

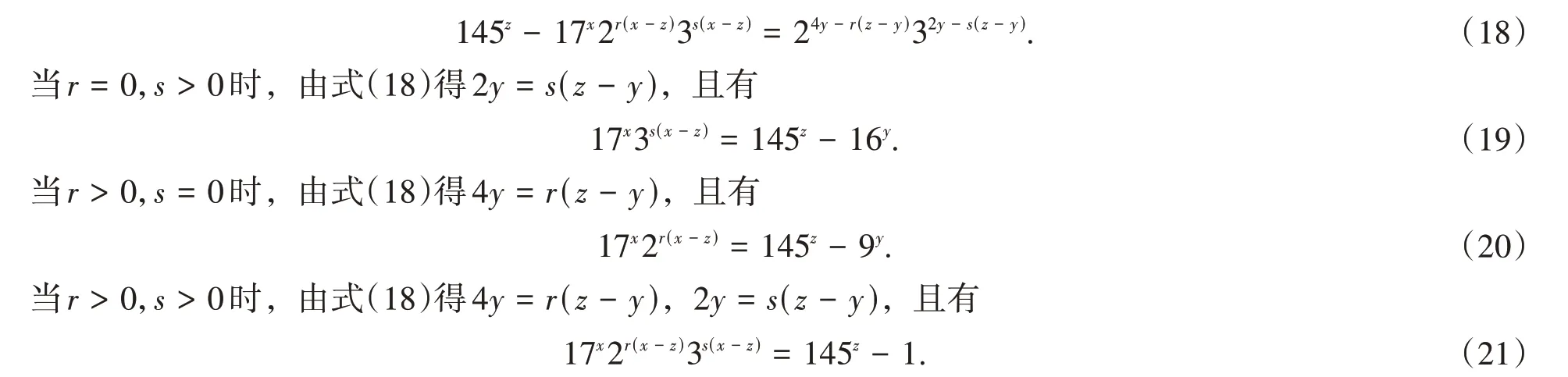
根据定理1的条件（iii），只需证z≡0(mod 2)时，方程（17）没有适合x＞z＞y以及n＞1的解(x，y，z，n)即可。

若式（19）成立，则对式（19）取模17，有9z≡(-1)y(mod 17)，即81z≡1(mod 17)，得z≡0(mod 4)，当然有z≡0(mod 2).

若式（20）成立，则对式（20）取模8 知，2r(x-z)≡0(mod 8)，故r(x-z) ≥3. 假定r(x-z) = 3，则r= 1或3. 当r= 1 时，z= 5y. 因8 012 167 577|(1455- 9)，而8 012 167 577|17x2r(x-z)，故式（20）不成立。当r=3时，3z= 7y，于是z= 7k，y= 3k，这里k∈N*. 因73|(1457- 93)，而73|17x2r(x-z)，故式（20）不成立。从而r(x-z) ≥4. 对式（20）取模16，有1 ≡9y(mod 16)，得y≡0(mod 2). 对式（20）取模17，有9z≡9y(mod 17)，即9z-y≡1(mod 17)，得z-y≡0(mod 8)，故z≡y≡0(mod 2).

若式（21）成立，则对式（21）取模17，有9z≡1(mod 17)，得z≡0(mod 8)，当然有z≡0(mod 2).

因此方程（17）仅有解x=y=z= 2.

（B） 当k= 11时，(a，b，c) =(23，264，265). 此时方程（1）成为

易知，方程（22）没有适合y＞z＞x以及n＞1 的解(x，y，z，n). 设方程（22）有适合x＞z＞y以及n＞1 的解(x，y，z，n). 由于b= 23· 3 · 11，故n= 2r3s11t（r，s，t∈N*，r+s+t≥1），于是方程（22）可化为

根据定理1 的条件（i）、（iii）～（v），只需证式（24）～（26），（28）～（29）中z≡y≡0(mod 2)和式（27）中z≡0(mod 3)以及式（30）中z≡0(mod 2)时，方程（22）没有适合x＞z＞y以及n＞1的解(x，y，z，n)即可。

若式（24）成立，则对式（24）取模11，有1 ≡2y(mod 11)，由Legendre符号的性质得1 =(2|11)y=(-1)y，故y≡0(mod 2). 再对式（24）取模5，有3x≡(-1)y≡1(mod 5)，得x≡0(mod 4). 故x≡y≡0(mod 2). 易知265 = 122+ 112= 162+ 32，且24 中2 的 方 幂3 大 于12 中2 的 方 幂2，根 据 定 理1 的 条 件（v），有z≡y≡0(mod 2).

若式（25）成立，则对式（25）取模23，有12z≡19y(mod 23)，由Legendre 符号的性质得1 =(12|23)z=(19|23)y=(-1)y，故y≡0(mod 2). 对式（25）取模5，有3x+s(x-z)≡-3y(mod 5)，由Legendre 符 号 的 性 质 得(-1)x+s(x-z)=(3|5)x+s(x-z)=(-3y|5) = 1，故x与s(x-z)同奇同偶。

对式（25）取模8，有(-1)x· 3s(x-z)≡1(mod 8). 假定s(x-z) ≡1(mod 2)，则得(-1)x· 3 ≡1(mod 8)，不可能。故x≡s(x-z) ≡0(mod 2). 类似式（24）的讨论知z≡y≡0(mod 2).

若式（26）成立，则对式（26）取模23，有12z≡10y(mod 23)，由Legendre 符号的性质得1 =(12|23)z=(10|23)y=(-1)y，故y≡0(mod 2). 对式（26）取模8，有(-1)x· 2r(x-z)≡0(mod 8)，得r(x-z) ≥3. 假定r(x-z) = 3，则r= 1或3.

当r= 1 时，z= 4y. 此 时 式（26）成 为 23x2x-4y= 2654y- 33y. 易 知 3 593|(2654- 33)， 故3 593|(2654y-33y)，而3 593|23x2x-4y，所以式（26）不成立。

当r= 3 时，z= 2y. 此时式（26）成为23x23(x-2y)= 2652y- 33y. 易知41|(2652- 33)，故41|(2652y- 33y)，而41|23x23(x-2y)，所 以 式（26）不 成 立。于 是r(x-z) ≥4. 对 式（26）取 模16，有9z≡1(mod 16)，得z≡0(mod 2). 故z≡y≡0(mod 2).

若式（27）成立，则对式（27）取模3，有1 ≡(-1)y(mod 3)，得y≡0(mod 2).

当s= 1 时，z= 2y. 此时式（27）成为23x3x-2y11t(x-2y)= 2652y- 8y. 易知7|(2652- 8)，故7|(2652y- 8y)，而7|23x3x-2y11t(x-2y)，所以式（27）不成立。于是s≥2. 对式（27）取模9，有4z≡(-1)y≡1(mod 9)，得z≡0(mod 3).

若 式（28）成 立， 当r= 1 时，z= 4y. 此 时 式（28）成 为23x2x-4y11t(x-4y)= 2654y- 3y. 易 知29 927|(2654- 3)，故29 927|(2654y- 3y)，而29 927|23x2x-4y11t(x-4y)，所以式（28）不成立。于是r≥2. 对式（28）取模4，有1 ≡(-1)y(mod 4)，得y≡0(mod 2).

假定z≡1(mod 2)，则由3y=r(z-y)，y=t(z-y)知r≡t≡0(mod 2).

对式（28）取模5，有3x· 2r(x-z)≡-3y(mod 5)，由Legendre符号的性质得

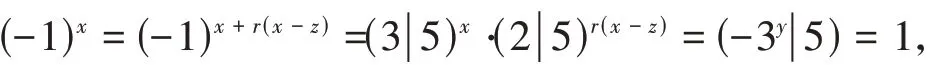
故x≡0(mod 2). 于是x≡r(x-z) ≡t(x-z) ≡0(mod 2). 类似式（24）的讨论知

若 式（29）成 立， 则 对 式（29）取 模23， 有12z≡11y(mod 23)， 由Legendre 符 号 的 性 质 得1 =(12|23)z=(11|23)y=(-1)y， 故y≡0(mod 2). 假 定z≡1(mod 2)， 则 由3y=r(z-y)，y=s(z-y) 知r≡s≡0(mod 2).

再对式（29）取模5，有3x2r(x-z)3s(x-z)≡-1(mod 5)，由Legendre符号的性质得

故x≡0(mod 2). 于是x≡r(x-z) ≡s(x-z) ≡y≡0(mod 2). 类似式（24）的讨论知

若式（30）成立，则对式（30）取模8，有23x2r(x-z)3s(x-z)11t(x-z)≡0(mod 8)，得r(x-z) ≥3. 假定r(x-z) = 3，则r= 1 或3. 仿式（26）的讨论知，式（30）不成立，故r(x-z) ≥4. 对式（30）取模16，有9z≡1(mod 16)，得

因此方程（22）仅有解x=y=z= 2.

（C） 当k= 12时，(a，b，c) =(25，312，313). 此时方程（1）成为

易知，方程（31）没有适合y＞z＞x以及n＞1 的解(x，y，z，n). 设方程（31）有适合x＞z＞y以及n＞1 的解(x，y，z，n). 由于b= 23· 3· 13，故n= 2r3s13t（r，s，t∈N*，r+s+t≥1），于是式（31）可化为

当r＞0，s＞0，t＞0时，由式（32）得3y=r(z-y)，y=s(z-y) =t(z-y)，且有

若式（36）～（38）成立，则由(313|5) =(8|5) =(3|5) =(13|5) = - 1结合定理1的条件（ii）知，方程（31）没有适合x＞z＞y以及n＞1 的解(x，y，z，n). 再根据定理1 的条件（i）和（iii），只需证式（33）～（35）中z≡y≡0(mod 2)和式（39）中z≡0(mod 2)时，方程（31）没有适合x＞z＞y以及n＞1的解(x，y，z，n)即可。

若式（33）成立，则对式（33）取模13，有1 ≡(-2)y(mod 13)，得y≡0(mod 12). 再对式（33）取模5，有3z≡(-1)y≡1(mod 5)，得z≡0(mod 4).故z≡y≡0(mod 2).

若式（34）成立，则对式（34）取模3，有1 ≡(-1)y(mod 3)，得y≡0(mod 2). 再对式（34）取模5，有3z≡(-1)y≡1(mod 5)，得z≡0(mod 4).故z≡y≡0(mod 2).

若式（35）成立，则当r= 1 时，z= 4y. 此时式（35）成为25x2x-4y= 3134y- 39y. 易知347|(3134- 39)，故347|(3134y- 39y)，而347|25x2x-4y，所以r≥2. 对式（35）取模4，有1 ≡(-1)y(mod 4)，得y≡0(mod 2).再对式（35）取模5，有3z≡(-1)y≡1(mod 5)，得z≡0(mod 4). 故z≡y≡0(mod 2).

若式（39）成立，则对式（39）取模5，有3z≡1(mod 5)，得z≡0(mod 4)，当然有z≡0(mod 2).

因此方程（31）仅有解x=y=z= 2.

（D） 当k= 13时，(a，b，c) =(27，364，365). 此时方程（1）成为

(27n)x+(364n)y=(365n)z，x，y，z∈N*. （40）

易知，方程（40）没有适合y＞z＞x以及n＞1 的解(x，y，z，n). 设方程（40）有适合x＞z＞y以及n＞1 的解(x，y，z，n). 由于b= 22· 7 · 13，故n= 2r7s13t（r，s，t∈N*，r+s+t≥1），于是方程（40）可化为

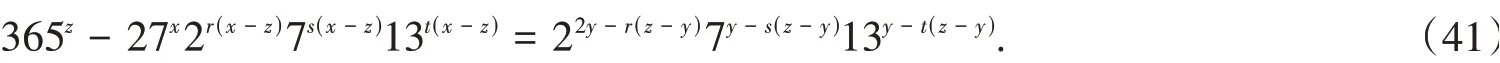
当r=s= 0，t＞0时，由式（41）得y=t(z-y)，且有

当r=t= 0，s＞0时，由式（41）得y=s(z-y)，且有

当s=t= 0，r＞0时，由式（41）得2y=r(z-y)，且有

当r= 0，s＞0，t＞0时，由式（41）得y=s(z-y) =t(z-y)，且有

当s= 0，r＞0，t＞0时，由式（41）得2y=r(z-y)，y=t(z-y)，且有

当t= 0，r＞0，s＞0时，由式（41）得2y=r(z-y)，y=s(z-y)，且有

当r＞0，s＞0，t＞0时，由式（41）得2y=r(z-y)，y=s(z-y) =t(z-y)，且有

根据定理1 的条件（i）和（iii），只需证式（42）～（44），（46）～（47）中z≡y≡0(mod 2)和式（45），式（48）中z≡0(mod 2)时，方程（40）没有适合x＞z＞y以及n＞1的解(x，y，z，n)即可。

若式（42）成立，则对式（42）取模3，有(-1)z≡1(mod 3)，得z≡0(mod 2). 对式（42）取模13，有1 ≡2y(mod 13)，得y≡0(mod 12).故z≡y≡0(mod 2).

若式（43）成立，则对式（42）取模3，有(-1)z≡1(mod 3)，得z≡0(mod 2). 对式（43）取模7，有1 ≡3y(mod 7)，得y≡0(mod 6).故z≡y≡0(mod 2).

若式（44）成立，则对式（44）取模3，有(-1)z≡1(mod 3)，得z≡0(mod 2).

当r= 1 时，z= 3y. 此时式（44）成为27x2x-3y= 3653y- 91y. 易知31|(3653- 91)，故31|(3653y- 91y)，而31|27x2x-3y，所以r≥2. 对式（44）取模4，有1 ≡(-1)y(mod 4)，得y≡0(mod 2). 故z≡y≡0(mod 2).

若式（45）成立，则对式（45）取模3，有(-1)z≡1(mod 3)，得z≡0(mod 2).

若式（46）成立，则对式（46）取模3，有(-1)z≡1(mod 3)，得z≡0(mod 2). 对式（46）取模13，有1 ≡7y(mod 13). 由Legendre符号的性质得1 =(7|13)y=(-1)y，即y≡0(mod 2). 故z≡y≡0(mod 2).

若式（47）成立，则对式（47）取模3，有(-1)z≡1(mod 3)，得z≡0(mod 2). 对式（47）取模7，有1 ≡(-1)y(mod 7)，得y≡0(mod 2).故z≡y≡0(mod 2).

若式（48）成立，则对式（48）取模3，有(-1)z≡1(mod 3)，得z≡0(mod 2).

因此方程（40）仅有解x=y=z= 2.

（E） 当k= 14时，(a，b，c) =(29，420，421). 此时方程（1）成为

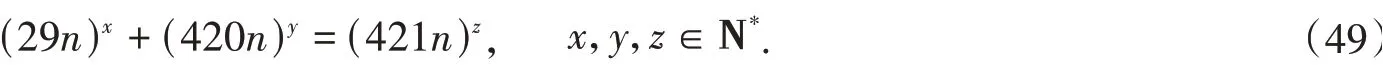
易知，方程（49）没有适合y＞z＞x以及n＞1 的解(x，y，z，n). 设方程（49）有适合x＞z＞y以及n＞1 的解(x，y，z，n). 由于b= 22· 3 · 5 · 7，故n= 2r3s5t7w（r，s，t，w∈N*，r+s+t+w≥1），于是方程（49）可化为

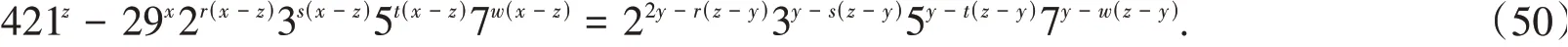
若式（51）～（52），（55），（58）～（59），（62）成立，则由(421|29) =(60|29) =(84|29) =(12|29)=(15|29) =(21|29) =(3|29) = -1. 结合定理1 的条件（ii）知，方程（49）没有适合x＞z＞y以及n＞1 的解(x，y，z，n). 再根据定理1 的条件（i）和（iii），只需证式（53）～（54），（56）～（57），（60），（63）～（64）中z≡y≡0(mod 2)和式（61），式（65）中z≡0(mod 2)时，方程（49）没有适合x＞z＞y以及n＞1的解(x，y，z，n)即可。

若式（53）成立，则对式（53）取模3，有1 ≡(-1)y(mod 3)，得y≡0(mod 2). 对式（53）取模29，有15z≡(-5)y(mod 29). 由Legendre 符 号 的 性 质 得(-1)z=(15|29)z=(-5|29)y= 1，故z≡0(mod 2). 于 是z≡y≡0(mod 2).

若式（54）成立，则对式（54）取模4，有2r(x-z)≡0(mod 4)，故r(x-z) ≥2. 假定r(x-z) = 2，则r= 1或2. 当r= 1 时，z= 3y. 因18 654 589|(4213- 105)，而18 654 589|29x2r(x-z)，故式（54）不成立。当r= 2时，z= 2y. 因11 071|(4212- 105)，而11 071|29x2r(x-z)，故式（54）不成立。从而r(x-z) ≥3. 对式（54）取模8，有(-3)z≡1(mod 8)，得z≡0(mod 2). 再对式（54）取模29，有15z≡18y(mod 29). 由Legendre 符号的性质得1 =(-1)z=(15|29)z=(18|29)y=(-1)y，故y≡0(mod 2). 于是z≡y≡0(mod 2).

若式（56），（60），（63）成立，则分别对式（56），（60），（63）取模3 和模29，类似式（53）的讨论知z≡y≡0(mod 2).

若式（57），（64）成立，则分别对式（57），（64）取模5和模29，类似式（53）的讨论知z≡y≡0(mod 2).

若式（61）成立，则对式（61）取模29，有15z≡4y(mod 29). 由Legendre 符号的性质得(-1)z=(15|29)z=(4|29)y= 1，故z≡0(mod 2).

若式（65）成立，则对式（65）取模29，类似式（61）的讨论知z≡0(mod 2).

因此方程（49）仅有解x=y=z= 2. 推论1得证。