紧优无向双环网络强彩虹连通数的下界估计*

刘杰，陈宝兴，钟玮

1. 闽南师范大学计算机学院，福建 漳州 363000

2. 三明医学科技职业学院，福建 三明 365000

3. 福建省高等学校数据与智能应用重点实验室，福建 漳州 363000

设G是非平凡连通图，可定义图为G=(V，E)，其中顶点集和边集分别用V(G)，E(G)表示。图的连通性有广泛的实际应用，比如通信网络的结构可以用图来表示，其中顶点代表不同的处理机或用户，边集代表了通信线路，构造出可靠最优的通信网络具有很强的实用价值，这些问题可抽象为图的问题来研究。2008 年Chartrand 等［1］首次提出了图的彩虹连通性的概念，作为此概念的一种加强，他们在此论文中也介绍了强彩虹连通的概念。关于图的（强）彩虹连通方面的一些定义，请读者参考文献［2］。

双环网络是计算机互联网络、大规模并行处理系统和通信系统的一类重要拓扑结构，双环网络最优直径策略研究以及双环网络最优构造法等方面受到许多学者的重视［2-6］，并得出不少结论。由于图的彩虹连通数在网络安全与密码管理中有重要的应用，而决定图的彩虹连通数问题是NP困难的，因此彩虹连通图的着色方法近几年来已成为图论的热门研究问题［1，7-9］，文献［10］得出一类边染色临界图的独立数。文献［11］探究了线性多边形链彩虹着色问题。文献［12］给出了某类含圈图的修正的彩虹顶点连通数。文献［13］研究了三类特殊图的（强）彩虹连通数，并得到了它的精确值。文献[14]与文献[15]分别给出一类有向与无向环型网络彩虹连通一种着色方法，并确定了其彩虹连通数的一个上界。

众所周知，网络的强彩虹连通数必大于或等于该网络的直径。容易验证图1 所示的无向双环网络G(8；±1，± 3)，其强彩虹连通数等于该网络的直径2。本文对无向双环网络最短路径唯一表示问题进行刻画，给出了紧优无向双环网络具有最短路径表示的一个充要条件，最后证明了一类具有唯一最短路径表示的紧优无向双环网络，其强彩虹连通数必大于或等于该网络的直径加1。

1 定义及引理

设1 ≤h＜n，h≠n/2，无向双环网络G(n；±1，±h)可定义为无向图（V（G），E（G）），其中顶点集为V(G) ={0，1，2，…，n- 1}， 边 集 是E(G) ={j→j+ 1(modn)，j→j- 1(modn)，j→j+h(modn)，j→j-h(modn) |j= 0，1，2，…，n- 1｝. 图1G(8；±1，± 3)表示为有8个顶点的无向双环网络。

图1 无向双环网络G(8；±1，± 3)Fig. 1 Undirected double-loop network G(8;±1, ± 3)

对于双环网络G(n；±1，±h)，定义点j到点(j+ 1)(modn)的边为［+1］，点j到点(j- 1)(modn)的边为［-1］。点j到点(j+h)(modn) 的边为［+h］，点j到点(j-h)(modn) 的边为［-h］。若一条从点v1到点v2的路径，它包含x1个［+1］与x2个［-1］边，y1个［+h］与y2个［-h］边，则有l≡(j+x1-x2+y1h-y2h)(modn)，并且模等式成立和边的顺序无关，从而路径可表示为：x1[+1]+x2[-1]+y1[+h]+y2[-h].

设v1，v2是G(n；±1，±h)中的两个顶点，x1[+1]+x2[-1]+y1[+h]+y2[-h]为点v1到点v2的一条最短路径，那么x1、x2中至少有一个是0，y1、y2中至少有一个是0. 点v1到点v2最短路径的边仅含［+1］和［+h］，或仅含［-1］和［+h］，或仅含［+1］和［-h］或仅含［-1］和［-h］. 可表示为：x[+1]+y[+h]，这里x，y∈Z.

设x1[+1]+y1[+h]，x2[+1]+y2[+h]是从点v1到点v2的任意两条最短路径，且可推出(x1，y1)=(x2，y2)，则称从点v1到点v2的最短路径表示唯一。

若一个无向双环网络的任意两个结点间均有唯一的最短路径表示，则称此网络具有唯一最短路径表示。

例1 无向双环网络G(8；±1，± 3)，从0 到2 的最短路径可表示为：2[+1]+ 0[+3]，(-1)[+1]+ 1[+3]，或0[+1]+(-2)[+3]. 此网络不具有唯一最短路径表示。

文献［1］给出了由G(n；±t1，±t2)所确定同余方程最小非负解与交叉解的定义，并给出了G(n；±t1，±t2)直径公式，可参见定理1。

定义1称同余式

为无向双环网络G(n；±1，±h)所对应的同余方程。

定义2设a1，a2∈Z，若有同余式a1+a2h≡0(modn)，则称格点(a1，a2)为零格点。对于零格点

推论1给定G(n；±1，±h)，其中n，h是正整数，1 ≤h＜n，h≠n/2，同余方程（1）的最小非负解与交叉解分别为(u，v)与(-a，b).设d为网络G(n；±1，±h)的直径，则u+v≤2d+ 1，a+b≤2d+ 1.

2 主要结果

引理1给定G(n；±1，±h)，其中n，h是正整数，1 ≤h＜n，h≠n/2，同余方程（1）的最小非负解与交叉解分别为(u，v)与(-a，b).设G(n；±1，±h)具有唯一最短路径表示，则u+v与a+b均为奇数。

证明 设d为网络G(n；±1，±h)的直径。不妨设u≥v（当u＜v时类似可证）。现证明u+v为奇数，类似可证a+b为奇数。用反证法，若u+v为偶数，由定理1的推论，可知u+v≤2d.

令t=(u+v)/2. 因为u+v为偶数，所以u，v同时为偶数，或同时为奇数。不妨设u，v都是偶数。易证网络G(n；±1，±h)中从0 到(u/2) +(v/2)h的距离为t. 注意到(u/2)[+1] +(v/2)[+h]与-(u/2)[+1]-(v/2)[+h]均是从0到(u/2) +(v/2)h的最短路径。这与G(n；±1，±h)具有唯一最短路径表示矛盾！ 证毕

引理2给定G(n；±1，±h)，其中n，h是正整数，1 ≤h＜n，h≠n/2，同余方程（1）的最小非负解与交叉解分别为(u，v)与(-a，b).设d为网络G(n；±1，±h)的直径，G(n；±1，±h)具有唯一最短路径表示，则

（i）当u≥v时，有v=a，且u+b= 2d+ 2；

（ii）当u＜v时，有u=b，且a+v= 2d+ 2.

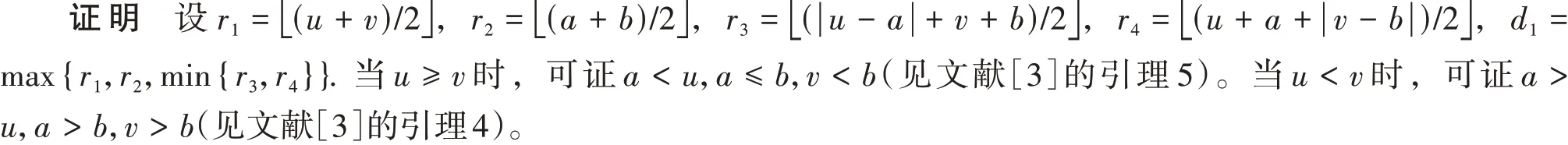
先证图G(n；±1，±h)具有唯一最短路径表示时，(u+a)(v+b) ≡1(mod 2) 并且r3=r4.

以下先证明u≥v的情形，当u＜v时，同理可证。

用反证法，若(u+a)(v+b) ≡1(mod 2)并且r3=r4不成立，由定理1可知d= max{r1，r2，min{r3，r4}}.因此min{r3，r4}≤d.

情形1：当r3≤r4时，可得r3≤d. 因为u+v与a+b均为奇数，所以u-a+v+b是偶数。从而u-a，v+b同时为偶数，或同时为奇数。不妨设u-a，v+b都是奇数。易证网络G(n；±1，±h)中从0 到(u-a+ 1)/2 +(v+b- 1)/2*h的 距 离 为r3≤d. 注 意 到(u-a+ 1)/2[+1] +(v+b- 1)/2*[+h] 与-(u-a-1)/2[+1]-(v+b+ 1)/2*[+h]均是从0 到(u-a+ 1)/2 + (v+b- 1)/2*h的最短路径。这与G(n；±1，±h)具有唯一最短路径表示矛盾！

情形2：当r4＜r3时，类似地，易证得与假设矛盾。

当(u+a)(v+b) ≡1(mod 2)并且r3=r4时，则G(n；±1，±h)的直径d=r3- 1，且u+v+a+b为偶数。

当u≥v时，因为

证明 注意到当网络G(n；±1，±h)是紧优的，且其直径为d时，有2d2- 2d+ 2 ≤n≤2d2+ 2d+ 1。

以下就u≥v情形给予证明。当u≥v时，可证得a≤b（见文献［3］的引理5）。

用反证法，若u+v≤d，因为

n=ub+va=ub+v2=u(2d+ 2 -u) +(u+v-u)2≤u(2d+ 2 -u) +(d-u)2=d2+ 2u≤d2+ 2d，注意到当d≥4时，n≤d2+ 2d<2d2- 2d+ 2，这与n≥2d2- 2d+ 2矛盾！

若a+b≤d，因为

n=ub+va=ub+a2=b(2d+ 2 -b) +(a+b-b)2≤b(2d+ 2 -b) +(d-b)2=d2+ 2b≤d2+ 2d，注意到当d≥4时，n≤d2+ 2d＜2d2- 2d+ 2，这与n≥2d2- 2d+ 2矛盾！

当u＜v时，类似可证结论u+v＞d且a+b＞d成立。

证明 必要性可由引理1和引理2得到。现证充分性，若G(n；±1，±h)不具有唯一最短路径表示，则存在一个结点i，使得从0到i的最短路径表示不唯一。不妨设u≥v（当u＜v时类似可证）。注意到d(0，i) ≤d.

设x1[+1]+y1[+h]，x2[+1]+y2[+h]是从0 到i的两个最短路径表示，这里(x1，y1)≠(x2，y2). 注意到(x1-x2，y1-y2)是零格点。

若x1-x2，y1-y2同号（同为正或同为负），不妨设x1-x2，y1-y2同为正。由引理3，可知2u+ 2v＞2d. 零格点(u-a，b+v)，(2u，2v)均在直线x+y= 2d的右侧，而且零格点(u+a，v-b)在第四象限中。与零格点C(u-a，b+v)相邻的4 个格点：B(u，v)，D(-a，b)，(u- 2a，2b+v)，(2u-a，b+ 2v)均是奇零格点（见图2）。

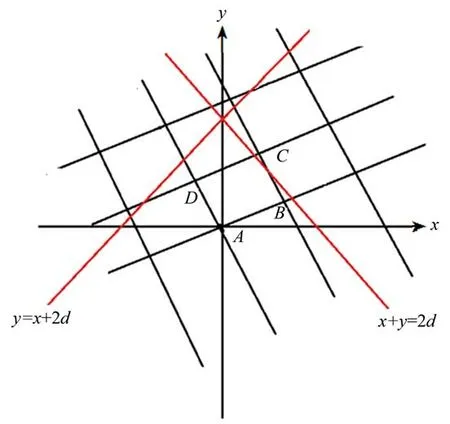
图2 零格点A(0，0)，B(u，v)，C(u - a，b + v)，D(-a，b)位置示意图Fig. 2 A location diagram of zero lattice points A(0,0),B(u,v),C(u - a,b + v),D(-a,b)

因为

因此(u- 2a，2b+v)，(2u-a，b+ 2v)均在直线x+y= 2d的右侧。因此在第一象限中，由x轴，y轴，及直线x+y= 2d围成的区域Ω 中，至多只有一个零格点(u，v)，(u，v)是一个奇零格点。因为x1-x2+y1-y2=2d(0，i) ≤2d，故偶零格点(x1-x2，y1-y2)在Ω中，这与区域Ω中不含偶零格点矛盾！

若x1-x2，y1-y2异号，不妨设x1-x2≤0，y1-y2≥0 . 由引理3，可知2a+ 2b＞2d. 因此零格点(-u-a，b-v)，(-2a，2b)均 在 直 线y=x+ 2d的 左 侧。与 零 格 点C(-u-a，b-v) 相 邻 的4 个 格 点：D(-a，b)，(-u，-v)，(-u- 2a，2b-v)，(-2u-a，b- 2v)均是奇零格点。且因为因此(-u- 2a，2b-v)，(-2u-a，b- 2v)均在直线y=x+ 2d的左侧。另外(-u，-v)在第三象限中。在第二象限中，由x轴，y轴，及直线y=x+ 2d围成的区域Σ 中，至多只有一个零格点(-a，b)，(-a，b)是一个奇零格点。因为-(x1-x2)+y1-y2= 2d(0，i) ≤2d，故偶零格点(x1-x2，y1-y2)在Σ 中，这与区域Σ 中不含偶零格点矛盾！ 证毕

引理5设t是一个正整数且2 ≤t＜n. 对于无向环形网络G(n；±1)，若t∤n，则使得G(n；±1)中长度不超过t的任一条路径都是彩虹路至少需要用t+ 1种颜色对G(n；±1)边着色。

证明 因为t∤n，可设n=pt+q，这里0 ＜q＜t. 若只用t种颜色对G(n；±1)边着色，从0 到t的路径是彩虹路，其路径上的t条边均应着不同的颜色，不妨设分别着色为1，2，…，t. 从1到t+ 1的路径也是彩虹路，因此t到t+ 1 的边应着色为1。从2 到t+ 2 的路径也是彩虹路，因此t+ 1 到t+ 2 的边应着色为2。因此从t到2t的路径上边的着色与从0到t的路径上的边着色相同，分别着色为1，2，…，t. 类似地，从2t到3t的路径上边的着色，……从(p- 1)t到pt的路径上边的着色，也应分别着色为1，2，…，t. 从pt到n的路径上边的着色，也应分别着色为1，2，…，q. 这导致了从pt到1 的路径上边的着色为1，2，…，q，1。从pt到1的路径不是彩虹路，其长度q+ 1 ≤t. 因此若仅使用t种颜色对G(n；±1)边着色，无法保证任一条长度不超过t的路径均是彩虹路。 证毕

推论2设t是一个正整数且2 ≤t＜n. 对于无向环形网络G(n；±h)，1 ≤h＜n，h≠n/2，若t∤n且t＜ngcd(n，h)，这里gcd(n，h)表示n，h的最大公因数，则使得G(n；±h)中长度不超过t的任何一条路径都是彩虹路至少需要用t+ 1种颜色对G(n；±h)边着色。

证明 记m=ngcd(n，h). 因t∤n，故t∤m. 因为网络G(n；±h)有gcd(n，h)个圈，每个圈的长度为m.对于网络G(n；±h)中的某个圈，与引理5的证明类似，至少需用t+ 1种颜色对这个圈的边进行着色。证毕

定理2给定G(n；±1，±h)，其中n，h是正整数，1 ≤h＜n，h≠n/2. 设d为网络G(n；±1，±h)的直径，且d∤n，d≥4，同余方程（1）的最小非负解与交叉解分别为(u，v)与(-a，b).若网络G(n；±1，±h)是紧优的，具有唯一最短路径表示，且u+v= 2d+ 1或a+b= 2d+ 1，则使得G(n；±1，±h)中任给两点间的最短路径有一条是彩虹路至少需用d+ 1种颜色对G(n；±1，±h)边着色。

证明 我们就当u≥v时给予证明（当u＜v时，类似可证）。因为u+v，a+b均为奇数，所以有u＞v，a＜b. 当u+v= 2d+ 1，可知u≥d+ 1。现证d(0，d) =d. 因为a=v≤d，所以d-a≥0。注意到格点(d-a，b)到4个零格点(0，0)，(u，v)，(u-a，b+v)，(-a，b)的距离分别为：d-a+b，d+ 2，d+ 1，d. 因为d-a+b＞d，(d-a) +bh≡d(modn)，所以d(0，d) =d. 因此从0到d的最短路径为：d[+1]+ 0[+h]. 从而在G(n；±1，±h)中从0到d，1到d+ 1，…，n-d到0，…，n- 1到d- 1的最短路径，与在G(n；±1)中的最短路径相同，据引理5 可知，则使得G(n；±1，±h)中任给两点间的最短路径有一条是彩虹路至少需用d+ 1种颜色对G(n；±1，±h)边着色。

当a+b= 2d+ 1，可知b≥d+ 1. 记m=ngcd(n，h). 现证d＜m. 若d≥m，因为mh≡0(modn)，所以(-a，b-m)是同余方程（1）的交叉解，这与(-a，b)是同余方程（1）的最小交叉解矛盾。

现证d(0，dh) =d. 因为v=a≤d，所以d-v≥0. 注意到格点(0，d)到4 个零格点(0，0)，(u，v)，(u-a，b+v)，(-a，b)的距离分别为：d，u+d-v，d+ 2，d+ 1. 因为u+d-v＞d，所以d(0，dh) =d. 因此从0到dh的最短路径为：0[+1]+d[+h]. 从而在G(n；±1，±h)中从0 到dh，1 到dh+ 1，…，n- 1 到dh- 1 的最短路径，与在G(n；±h)中的最短路径相同，据引理5 的推论2 可知，则使得G(n；±1，±h)中任给两点间的最短路径有一条是彩虹路至少需用d+ 1种颜色对G(n；±1，±h)边着色。 证毕

例2

（i）对于无向双环网络G(2t2+ 2t+ 1；±1，±(2t+ 1))（这里t是正整数，t≥4），同余方程（1）的最小非负解与交叉解分别是(t+ 1，t)、(-t，t+ 1). 利用定理1，易求得网络G(2t2+ 2t+ 1；±1，±(2t+ 1))的直径为t，因此网络G(2t2+ 2t+ 1；±1，±(2t+ 1))是紧优的。因为u=t+ 1，v=t，a=t，b=t+ 1，所以有u≥v，v=a，u+b= 2t+ 2，且u+v与a+b均是奇数。因此依据引理4，G(2t2+ 2t+ 1；±1，±(2t+ 1))具有唯一最短路径表示。注意到u+v= 2t+ 1，据定理2，G(2t2+ 2t+ 1；±1，±(2t+ 1))的强彩虹连通数至少是该网络的直径加1。

（ii）对于无向双环网络G(2t2+ 1；±1，±(2t2- 2t))（这里t是正整数，t≥4），同余方程（1）的最小非负解与交叉解分别是(t- 1，t)、(-t- 2，t- 1) . 利用定理1，易求得网络G(2t2+ 1；±1，±(2t2- 2t))的直径为t，因此网络G(2t2+ 1；±1，±(2t2- 2t))是紧优的。因为u=t- 1，v=t，a=t+ 2，b=t- 1，所以有u＜v，u=b，a+v= 2t+ 2，且u+v与a+b均是奇数。因此依据引理4，G(2t2+ 1；±1，±(2t2- 2t))具有唯一最短路径表示。注意到a+b=t+ 2 +t- 1 = 2t+ 1，据定理2，G(2t2+ 1；±1，±(2t2- 2t))的强彩虹连通数至少是该网络的直径加1。