度量空间上B*-隐式收缩条件和唯一公共不动点*

朴勇杰

延边大学理学院数学系，吉林 延吉 133002

令R+是非负实数集。2008年，Akram等[1]引进了一个满足以下条件的函数α：(R+)3→R+的集合的函数类A

（i）α在(R+)3是连续的；

（ii）存在实数k∈[0，1)使得对任意a，b∈[0，∞)，当a≤α(a，b，b)或a≤α(b，a，b)或a≤α(b，b，a)时有a≤kb.

同时，称实数空间X上的自映射T是A-收缩，是指存在α∈A使得对任意x，y∈X，有

他们利用这一新的收缩条件得到了若干重要的结果，所得结果推广和改进了Banach 收缩原理[2]，Kannan 不动点定理[3]及若干其他不动点定理，而Saha 等[4]于2012 年利用A-收缩把文献［1］的结果推广到积分型结果。文献［1］中指出A-收缩推广和改进了M-收缩[5]，K-收缩[2]，B-收缩[6]，R-收缩[7]及其他若干收缩。显然，A-收缩是如下收缩的推广

为了解决此问题，文献［12］作者在复值度量空间上引进一复值函数类B，并利用该函数类讨论了若干不动点和公共不动点问题，所得结果推广和改进了Chatterjea-型不动点定理和变形结果以及一些其他结果。但是B的定义中一个条件类似于α（ii），要求k∈[0，1). 当k∈[0，1)时利用柯西原理[13]判定序列的柯西性，而k= 1时由于复值度量空间上的偏序关系不是全序[9，12]，所以在k= 1的条件下复值度量空间上判定序列的柯西性是不容易的。于是在本文，将在实空间上定义B的推广概念并在k= 1 的条件下得到具有两个度量的集合上映射族的唯一公共不动点存在定理，并给出两个实例验证所得结论的正确性。

1 基本概念

2 唯一公共不动点

定理1设(X，d)和(X，δ)是两个度量空间，S，T：X→X是两个映射。假设

（i）对任意x，y∈X，d(x，y) ≤δ(x，y)；

（ii）(X，d)是完备的；

因此由定义1的条件（ii）得δ(z，Sz) = 0，从而Tz=z=Sz.

如果w也是T和S的公共不动点，则

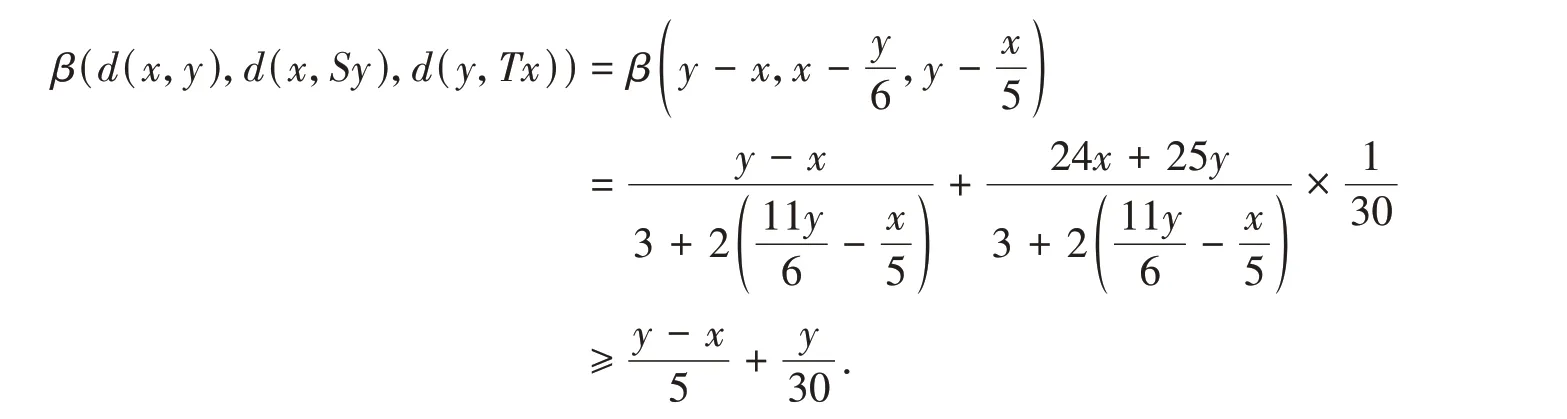
结合式（13）知式（1）成立，因此β，T，S满足定理1的所有条件，于是T和S有唯一公共不动点0.

注记1 如果定理1 中的(X，d)的完备性用(X，δ)的完备性代替，则条件（i）和（iii）是多余的。事实上，在定理1 中仅利用（iv）证明了{xn}在(X，δ)上是柯西的，因此存在z∈X使得{xn}在(X，δ)收敛于z. 根据式（1），

因此根据定义1的条件（ii）得Tz=z. 再由式（1）得

从而由定义1的条件（ii）得δ(z，Sz) = 0，于是Tz=z=Sz.

注记2 根据定理1和例1可知当定理1 中的β取为例1的函数时得到满足线性收缩条件的公共不动点定理，特别当a= 0，b=c或a=b=c时分别得到Chatterjea-型公共不动点定理或其变形结果。于是定理1推广和改进了很多已知的（公共）不动点定理。

“这真离奇。一个偷香窃玉的男人，找到真爱却又遭到抛弃而最终厌倦了女人。这个情场的浪子回头又太迟了。他遇到了一个女浪子。我想现实生活中不会有这样的男人。”

下列结果是定理1在非连续条件下的表现形式。

定理2设(X，d)和(X，δ)是两个度量空间，S，T：X→X是两个映射。假设

（i）对任意x，y∈X，d(x，y) ≤δ(x，y)；

（ii）(X，d)是完备的；

（iii）对任意x，y∈X，

从而根据定义1的条件（ii）得d(z，Sz) = 0，于是Tz=z=Sz. 公共不动点的唯一性的证明类似于定理1。

下列结果是定理1在两个度量空间的非完备条件及两个映射之一仅在一个空间的某一点处连续条件下的表现形式。

（i）对任意x，y∈X，d(x，y) ≤δ(x，y)；

（ii）存在一个点x0∈X及由满足条件x2n+1=Tx2n和x2n+2=Sx2n+1的序列{xn}的子序列{xni}在(X，d)上收敛于某点z∈X；

（iii）T或S在(X，d)的点z上连续；

（iv）对任意x，y∈X，

如果β具有P-性质，则S，T有唯一公共不动点。

（i）对任意x，y∈X，d(x，y) ≤δ(x，y)；

（ii）(X，d)是完备的；

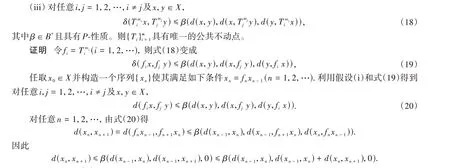
于是根据定义1的条件（ii）得

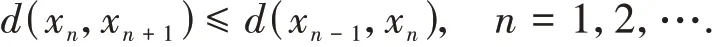
利用式（20）并采用定理1 的证明路线可以证明{xn}在(X，d)上是柯西的。于是根据假设（ii）存在z∈X使得

固定n= 1，2，…，且任取i∈N使得i＞n，则根据式（20）得