有限域上一类Carlitz方程的解数公式

陈钦龙,肖义丽,曹 炜,3

（1.闽南师范大学数学与统计学院,福建 漳州 363000；2.宁波大学数学与统计学院,浙江 宁波 315211；3.福建省粒计算及其应用重点实验室,福建 漳州 363000）

设Fq表示特征为p的q阶有限域,其中q=pr,p为素数,r∈Z+,F*q=Fq{0}.设f为Fq上具有如下形状的对角多项式

其中ai∈F*q,mi∈Z+,mi|(q-1),i=1,…,n.用Nq(f)表示方程f=0在Fq中的解数.1949年,华罗庚等[1]和Weil[2]分别独立地得到了Nq(f)用特征和表示的公式

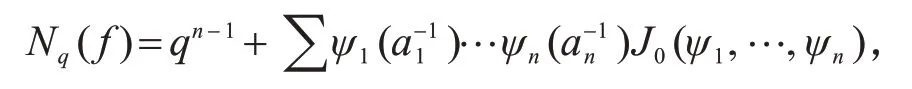
其中和项过所有满足ψmi i=ε,ψi≠ε,i=1,…,n且ψ1…ψn=ε的Fq上n个乘法特征ψ1,…,ψn,；ε表示Fq上的平凡乘法特征;J0(ψ1,…,ψn)为Fq上的雅可比和,即

1954年,Carlitz[3]首先提出寻找如下形式方程的解数问题

其中a1,…,an,b∈F*q,n≥3.对于n=3 和n=4,他给出了解数的具体表达式.Baoulina[4-8]推广了Carlitz 的相关结果,并对n,q进行限定,得到了方程式(2)满足特定条件时的解数公式.其他关于Carlitz类型方程及其推广形式的研究参见文献[9-14].Baoulina[7]研究了下列Carlitz方程

其中ai,b∈F*q,mi∈Z+,mi|(q-1),1≤i≤n,n≥2.

利用I(m1,…,mn)给出方程式(3)在特殊情形时解数公式的具体表达式,即

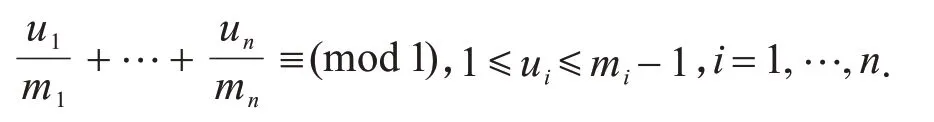
其中I(m1,…,mn)表示下列丢番图方程的解(u1,…,un)的个数.

1 引理

设ψ是Fq上的非平凡乘法特征,定义Fq上关于ψ的高斯和为

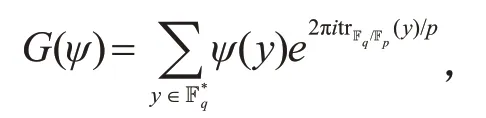
其中trFq/Fp(y)=y+yp+…+ypr-1表示y从Fq到Fp的绝对迹.

引理1[15]设ψ1,…,ψt,ε是Fq上的乘法特征,其中ε是平凡特征.则有

设1≤d|(q-1),令ℭdq={ad|a∈F*q},即表示F*q中的d次幂元集合.用N(xk=b)表示方程xk=b的解x∈Fq的个数,其中k∈Z+,b∈Fq.

引理2[15]令ψ是Fq上阶为d0=gcd(k,q-1)的乘法特征,则有

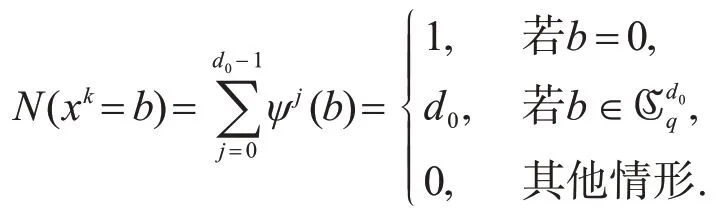
引理3[15]设q=p2ls,p是素数,l,s∈Z+.令ψ是Fq上阶为δ的乘法特征,且δ|(pl+1),则有

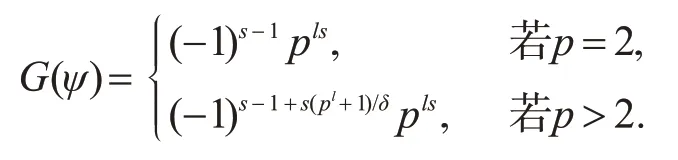
考虑下面的Carlitz方程

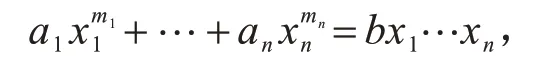
引理4设q=p2ls,p是素数,l,s∈Z+,ai=bmi i,i=1,…,n.设ψ是Fq上阶为δ的乘法特征,其中δ＞1,δ|d,mδ|(pl+1).令λ是Fq上阶为pl+1的乘法特征使ψ=λ(pl+1)/δ.则有

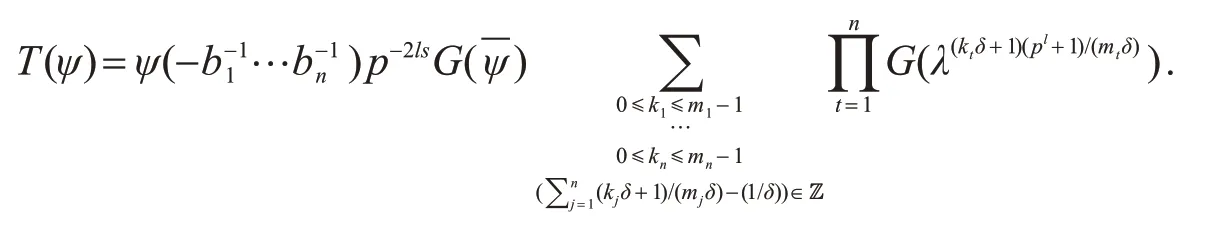
证明因为λ的阶为pl+1,故λ(pl+1)/mt的阶为mt,1≤t≤n.又已知mδ|(pl+1),所以mi|(pl+1)/δ.由引理2 有

因为mtδ∤(ktδ+1),其中0≤kt≤mt-1,1≤s≤n.所以λ(ktδ+1)(pl+1)/δmt≠ε.又因为ψ=λ(Pl+1)/δ,所以由引理1 可得结论.

引理5[16]设m1,…,mn∈Z+,m=lcm[m1,…,mn].则对θ∈Q,同余h式

有解当且仅当mθ∈Z,且在同余式有解时,其解数为

进一步,利用引理3,引理4 和引理5,我们可以得到T(ψ)的具体值.

引理6设q=p2ls,其中p是素数,l,s∈Z+,ai=bmi i,i=1,…,n.设ψ是Fq上阶为δ的乘法特征,其中δ＞1,δ|d,mδ|(pl+1).则有

证明首先我们先证明ψ(-1)=1.若p=2,则ψ(-1)=ψ(1)=1.若p＞2,且mδ|(pl+1),(pl+1)|(p2l-1),则2δ|(p2l-1),又因为(p2l-1)|(p2ls-1),所以2δ|(p2ls-1),因此ψ(-1)=(-1)(p2ls-1)/δ=1.

设g是循环群的生成元,λ是上 阶 为pl+1的乘法特征.定义ψ(g)=e2πi/δ,λ(g)=e2πi/(pl+1)故ψ=λ(pl+1)/δ.设kr∈Z,0≤kr≤mr-1,1≤r≤n,且因为mrδ∤(krδ+1),所以λ(krδ+1)(pl+1)/mrδ≠ε,且λ(krδ+1)(pl+1)/mrδ的阶为(pl+1)/(gcd(pl+1,(krδ+1)(pl+1)/(mrδ))).接下来证明

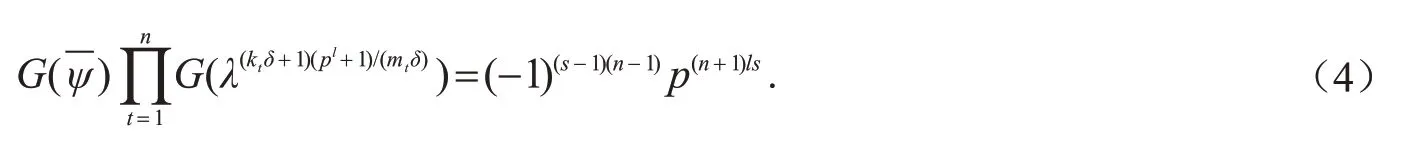
分两种情形进行讨论.

(i)若p或为偶数,则由引理3 可得

显然,此时式(4)对第一种情形成立.

(ii)若p和均为奇数,则由引理3 知只须证

对任意的1≤j≤n,有

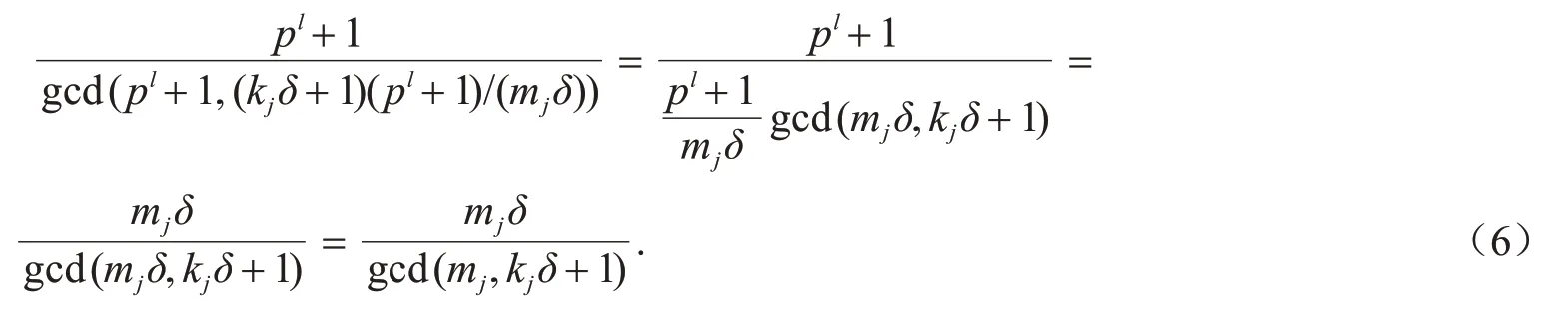
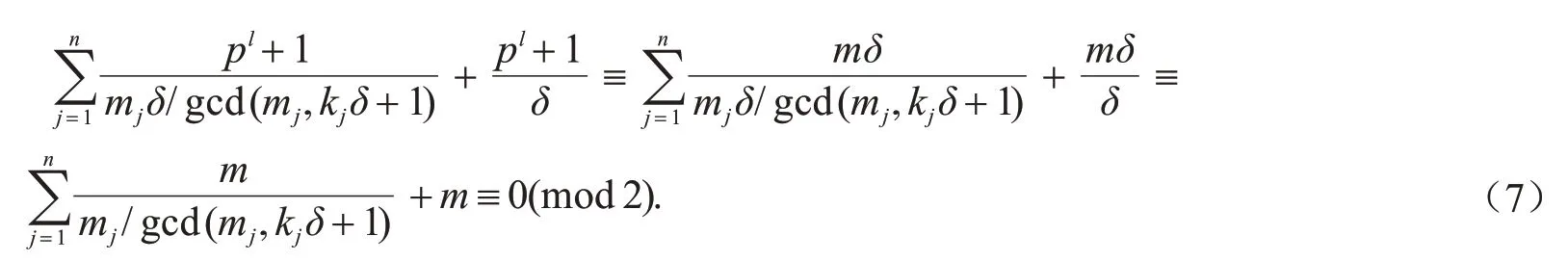
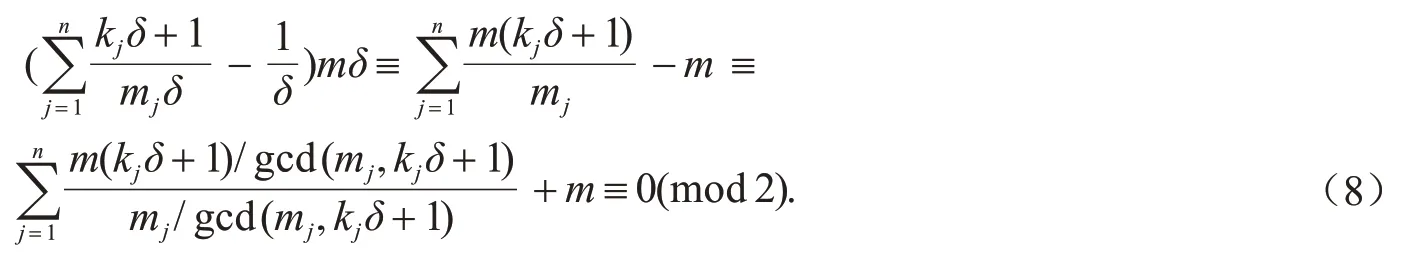
故由引理4 可得

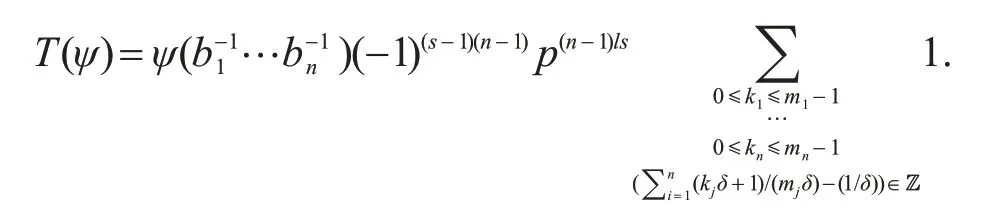
综上,引理得证.

2 主要结论及其证明

主要考虑下面的Carlitz 方程

其中mi∈Z+,mi|(q-1),ai∈,b∈F*q,1≤i≤n,n≥2.设用Nq表示方程式(10)在Fq中的解数.用Nq(0)和Nq*(0)分别表示方程a1xm11+…+anxmnn=0在Fq和在F*q中的解数.

定理1[1-2]设f是形如式(1)的多项式,则

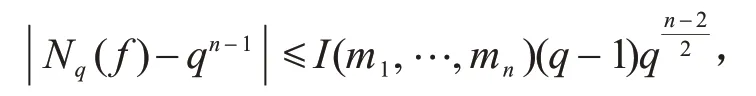
其中I(m1,…,mn)表示下列丢番图方程的解(u1,…,un)的个数

定理2[7]设ψ是有限域Fq上的乘法特征,则方程式(3)在Fq中的解数为

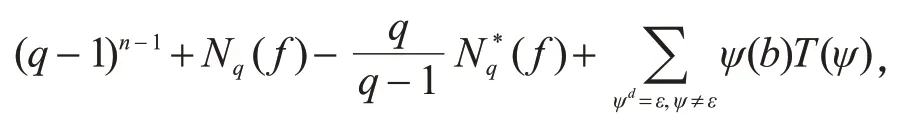
其中

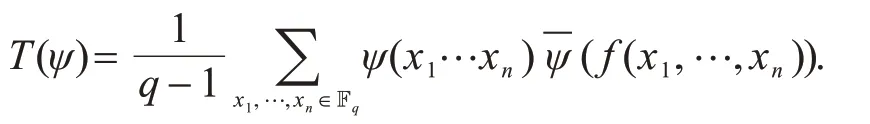
定理3设q=p2ls,其中p是素数,l,s∈Z+.若m|(pl+1),则有

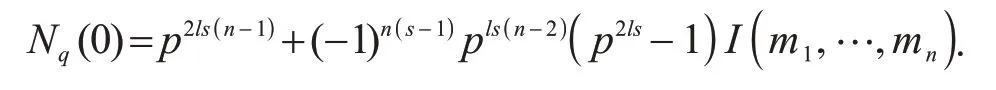
证明λ是Fq中阶为pl+1 的乘法特征,则λ(pl+1)/mi在Fq中的阶为mi,其中1≤i≤n.因为所以方程与方程ym11+…+ymnn=0的解数相同.由引理1 和引理2 有

类似引理6 中对式(4)的证明,可以得到

故由式(11)和式(12)可得

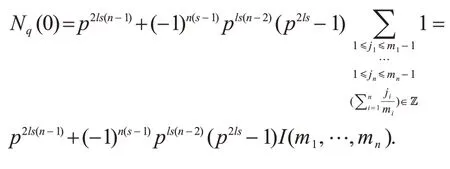
即证.

定理4设q=p2ls,其中p是素数,设md＞2,且有md|(pl+1),其中l选择最小整数,则

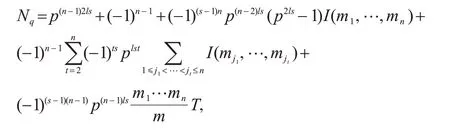
其中

证明由定理3 与容斥原理可得

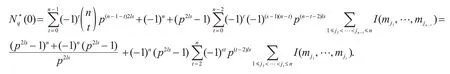
由定理2 和定理3 可得

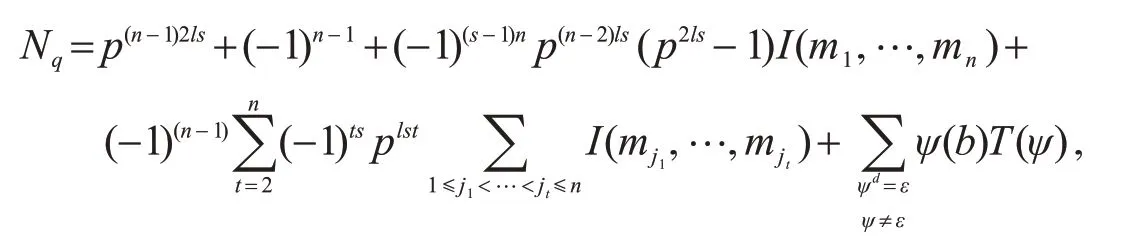
最后由引理6 得

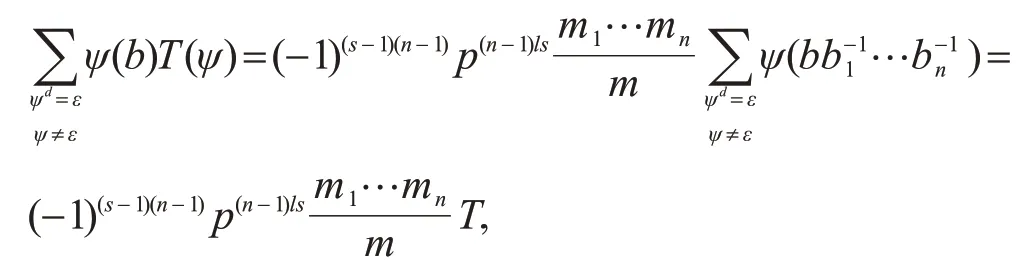
其中T的定义可由引理2 得到.