一类新的广义模糊软集及其在多属性决策中的应用

江立辉, 马成芸, 陈华友

(1.合肥学院 人工智能与大数据学院, 安徽 合肥 230601; 2.安徽大学 数学科学学院, 安徽 合肥 230039)

0 引言

自从Zadeh于1965年提出模糊集理论之后,有关模糊集理论的研究引起了广大学者的关注,直觉模糊集、区间值直觉模糊集、区间值犹豫模糊集等新的概念先后被提出来.对偶犹豫模糊集因为包含了隶属犹豫函数和非隶属犹豫函数两个部分,可以更加灵活地为域中的每个元素赋值,因此能够更加客观地反映实际情况[1].模糊软集是另一种模糊信息的表现形式,它为模糊环境下的决策研究打开了一扇新的窗户.软集理论自提出以来得到了极大的丰富,包括区间值模糊软集、区间值直觉模糊软集、对偶犹豫模糊软集、广义模糊软集、区间值对偶犹豫模糊软集、广义区间值直觉模糊软集、双极值直觉模糊软集等理论[2-11]被先后提出.距离和相似度是不确定性度量中的两个重要的概念,是确定两个对象之间关系的重要工具.2011年，Xu和Xia研究了犹豫模糊集的距离和相似度量公理化公式[12],王超在此基础上提出了基于Hamming距离和Euclidean距离区间值对偶犹豫模糊软集的相似性度量[7].黄鹤基于三种犹豫模糊集的包含度提出了广义犹豫模糊软集的相似度量公式，并构造了一种决策方法[13].

本文在上述研究的基础上,将区间值对偶犹豫模糊集与广义模糊软集相结合,提出了一型和二型广义区间值对偶犹豫模糊软集的概念,定义其交、并、补、“且”、“或”的运算,证明了相应的性质.此外,基于二型广义区间值对偶犹豫模糊软集的距离测度,研究了它的相似性度量及其性质.最后,提出了一种基于二型广义区间值对偶犹豫模糊软集相似度的多属性决策方法,并通过实例说明了该方法的可行性和有效性.

1 基本概念

定义1[6]设U是一个初始论域,E是一个参数集,P(U)表示U的幂集,A⊆E,F:A→P(U)是一个映射,μλ是A的模糊子集,即μλ:A→[0,1].定义映射Fλ:A→P(U)×[0,1],对∀e∈A,有Fλ(e)=(F(e),μλ(e)).其中F(e)∈P(U),μλ∈[0,1],则称Fλ是软论域(U,E)上的广义模糊软集.

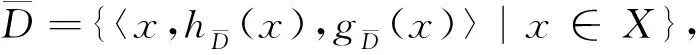
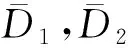
2 广义区间值对偶犹豫模糊软集

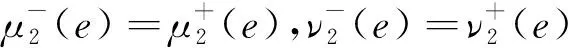
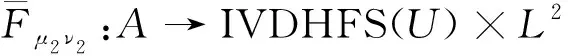
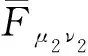
1)A⊆B;

3) 〈μ2,ν2〉是〈δ2,ε2〉的子集,即∀ej∈A,μ2(ej)≤δ2(ej)且ν2(ej)≥ε2(ej).

其中,函数σ(θ):(1,2,…,s)→(1,2,…,s)是一个序列,满足hσ(θ)(x)≤hσ(θ+1)(x)(θ=1,2,…,s-1),即hσ(θ)是h中第θ大的值,s是h(xi,ej)中元素的个数;函数ζ(η):(1,2,…,t)→(1,2,…,t)是一个序列,满足gζ(η)≤gζ(η+1)(η=1,2,…,t-1),即gζ(η)是g中第η大的值,其中t是g(xi,ej)中元素的个数.

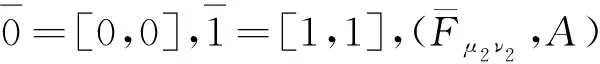
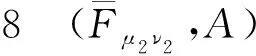
根据定义8易得下述定理．

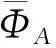
下面给出广义区间值对偶犹豫模糊软集交和并的定义．

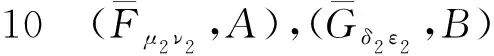
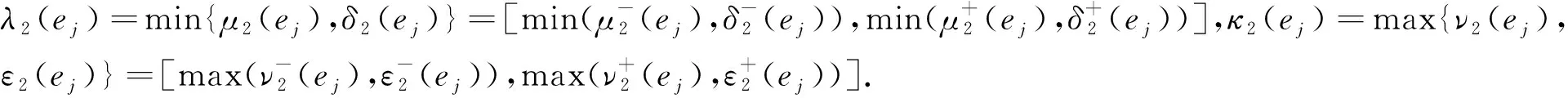
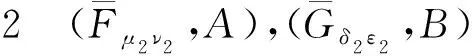
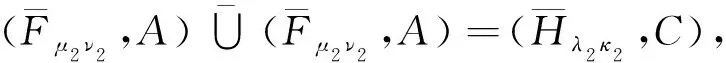
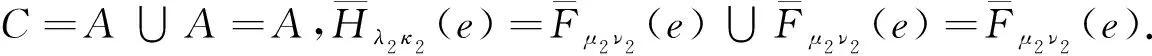
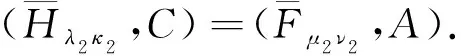
同理可证,式(2)～(6)也成立.

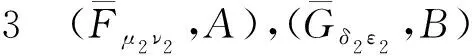
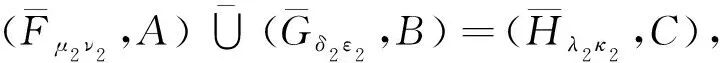
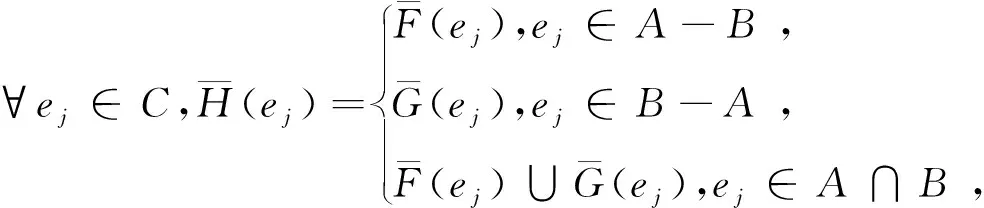
λ2H(ej)=max{μ2(ej),δ2(ej)},κ2H(ej)=min{ν2(ej),ε2(ej)},

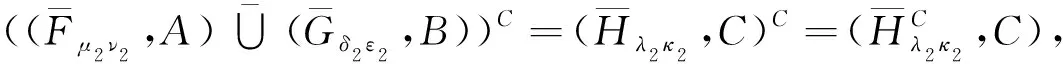
λ2HC(ej)=min{ν2(ej),ε2(ej)},κ2HC(ej)=max{μ2(ej),δ2(ej)},

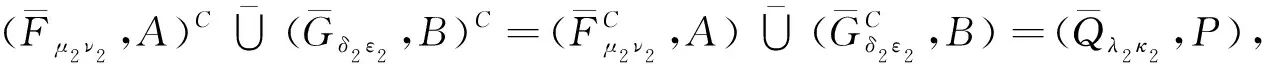
λ2Q(ej)=max{ν2(ej),ε2(ej)},κ2Q(ej)=min{μ2(ej),δ2(ej)},

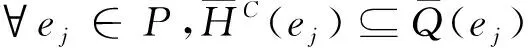
同理可证2)成立.

证明证明过程参考文[14]，可到得结论.

证明参见引文[14]的方法,容易证得结论．

下面给出广义区间值对偶犹豫模糊软集“且”、“或”的定义.

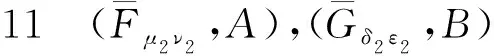
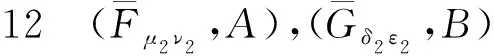
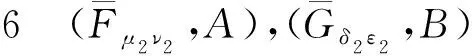
证明可参照文[14]，此处略.

3 广义区间值对偶犹豫模糊软集的相似度量

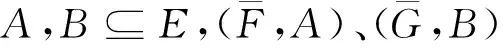
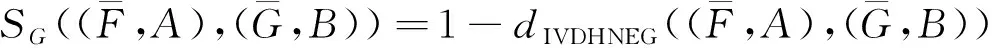
(1)

其中

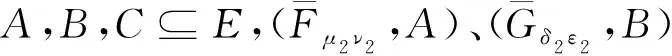
则称映射S为广义区间值对偶犹豫模糊软集的相似度量.

定理7 广义区间值对偶犹豫模糊软集的相似度量公式为

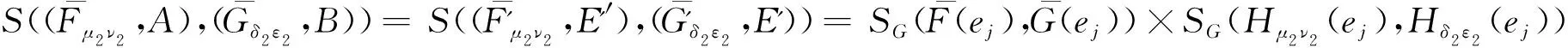
(2)

其中Hμ2ν2(ej)=(μ2(ej),ν2(ej)),Hδ2ε2(ej)=(δ2(ej),ε2(ej)).

证明1) 显然成立;

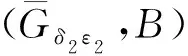
根据定义6,有

μ2(ej)≤δ2(ej)≤ω2(ej)且ν2(ej)≥ε2(ej)≥θ2(ej).

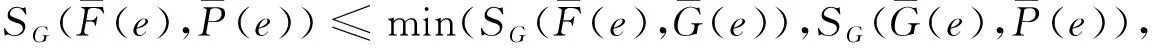
SG(Hμ2ν2(ej),Hω2θ2(ej))≤min(SG(Hμ2ν2(ej),Hδ2ε2(ej)),SG(Hδ2ε2(ej),Hω2θ2(ej)))

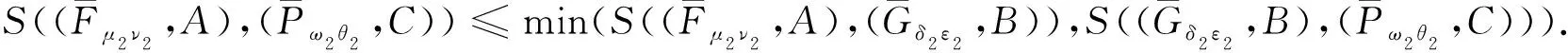
4 基于广义区间值对偶犹豫模糊软集的多属性决策方法

相似度量在决策、模式识别、机器学习和市场预测等许多领域中都非常重要,现有文献在这方面也做了大量的研究.本节在广义区间值对偶犹豫模糊软集基础上提出新的相似度量的概念,并基于此构建一种新的决策方法.

对于一个多属性决策问题, 设U={x1,x2,…,xn}是一个初始论域,E={e1,e2,…,en}是一个参数集.首先构造广义区间值对偶犹豫模糊软集正理想解和负理想解,表达式如下

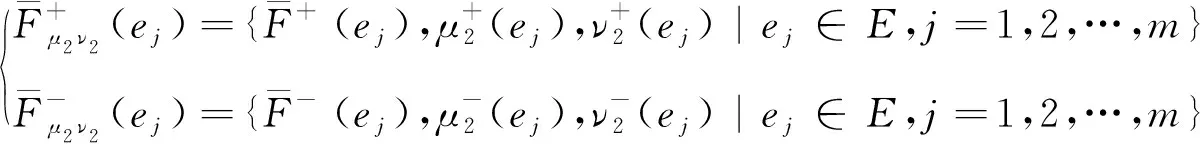
(3)

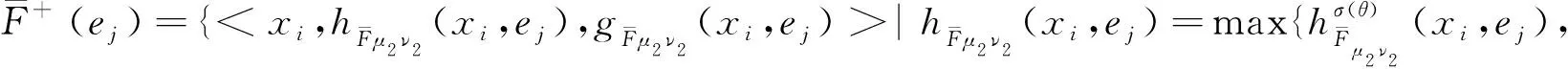
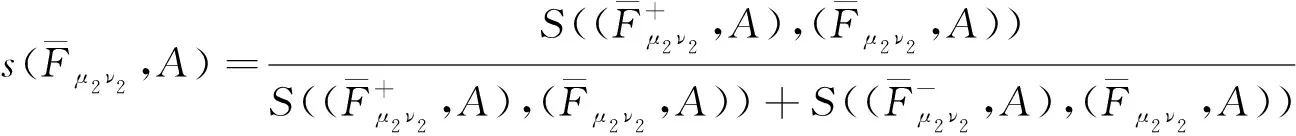
(4)

显然0≤s≤1,并且s的值越大,相应的备选方案就越好.因此,可以通过s来对备选方案进行排序,从而得到最佳备选方案.上述方法可归纳结为下面步骤.

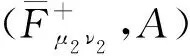
步骤5: 通过排序选择出最佳备选方案.

5 算例分析

随着全球经济一体化进程的推进,能源成为制约经济社会发展的重要因素,如何选择合适的能源项目对一个地区的经济发展和环境保护有着十分重要的意义．某地计划对5个能源项目U={x1,x2,x3,x4,x5}进行投资评估,参数集E={e1,e2,e3,e4}分别表示资源(e1)、生产(e2)、消费(e3)和环境(e4),通过专家评估,综合考虑这些因素后进行投资决策．

步骤1: 根据实际情况,将专家提供的决策信息构建广义区间值对偶犹豫模糊信息决策矩阵,包含各项目的属性值及属性权重．如表1所示．

表1 能源项目评分表

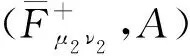
表2 不同参数下备选项目的相似度及排序

从计算结果可以看出,随着参数λ的变化,项目的排序也会产生变化,但最优项目的选择基本稳定,始终有x5和x3这两个项目优于其他备选项目,故建议选择项目x5进行投资.

6 小结

广义区间值对偶犹豫模糊软集可以更多地表述决策者的犹豫态度,它不仅能够描述元素xi属于论域U的程度,还考虑到了参数ej的犹豫情况,是现有软集理论的一种扩充.文章定义了广义区间值对偶犹豫模糊软集的交、并、补、“且”、“或”运算及性质,提出了相关定理,同时对其进行了证明．此外,研究了该软集的相似度量,并给出了基于广义区间值对偶犹豫模糊软集的多属性决策方法.最后,通过实例验证了该方法的可行性和有效性.