q-阶正交区间模糊Einstein集成算子及其应用

杜玉琴，孙 超，崔建新

(1.中国社会科学院大学 经济学院，北京 102488；2.中国传媒大学 数据科学与智能媒体学院，北京 100024；3.中铁投资集团有限公司，北京 100039)

由于社会环境的不确定性以及实际问题的复杂性和可变性，通常无法用明晰的数字来表示属性值，尤其是定性属性值。为了解决这个问题，Zadeh[1]提出了模糊集的概念，随后Atanassov[2]提出了直觉模糊集(Intuitionistic Fuzzy Sets, IFS)，它同时评估决策问题中支持和反对的替代方案。2013年，Yager等[3]给出了Pythagorean模糊集(Pythagorean Fuzzy Sets, PFS)的定义，其隶属度μ和非隶属度v之和可以大于1，并且满足条件0≤u2+v2≤1。与IFS相比，PFS的应用范围更广，PFS可以解决IFS无法解决的一些决策问题。之后，许多学者将PFS进一步扩展来解决多属性群决策问题[4-6]。

2017年，Yager[7]在IFS和PFS的基础上，结合文献[8-10]提出了q-阶正交模糊集(q-Rung Orthopair Fuzzy sets,q-ROF)的概念，其隶属度μ的q次幂和非隶属度v的q次幂之和要求小于等于1，即0≤uq+vq≤1。由于IFS和PFS都是q-ROF的特例，因此q-ROF在处理不确定信息等方面比IFS和PFS更具灵活性，更具有一般性，从而引起了国内外一些学者的关注。Liu等[11]定义了q-阶正交模糊加权平均(q-Rung Orthopair Fuzzy Weighted Average,q-ROFWA)算子和q-阶正交模糊加权几何(q-Rung Orthopair Fuzzy Weighted Geometry,q-ROFWG)算子。Liu等[12]将Bonferroni平均(Bonferroni Mean, BM)算子与q-阶正交模糊数(q-Rung Orthopair Fuzzy Numbers,q-ROFNs)相结合，提出了q-阶正交模糊BM(q-Rung Orthopair Fuzzy Bonferroni Mean,q-ROFBM)算子和q-阶正交模糊几何BM算子。Wang等[13]提出了q-阶正交区间模糊信息的多属性群决策方法，并将其应用于绿色供应商选择问题。Xing等[14]提出了一些q-阶正交模糊点加权集成算子，并将其用于解决多属性决策问题。

算子集成理论是模糊集理论中的一个重要组成部分，研究信息算子集成问题[15]具有一定的理论价值。由于Einstein T模和Einstein S模[16]是代数T模和S模的一种推广，应用更广泛，Zhang[17]定义了拟直觉模糊Einstein混合加权平均算子和拟直觉模糊Einstein混合加权几何平均算子。Yu等[18]提出了犹豫的模糊Einstein集成算子并将其应用到实际问题中。Liu等[19]提出了几种直觉不确定语言模糊powered Einstein信息集成算子。Garg[20]将Einstein T模和S模推广到了Pythagorean模糊环境中，定义了Pythagorean模糊Einstein加权平均(Pythagorean Fuzzy Einstein Weighted Average, PFEWA)算子。目前，对Einstein算子在q-阶正交模糊环境下的应用的研究尚处于起步阶段，Einstein算子在多属性群决策的应用还很少见。

随着互联网的发展，科学技术的进步，人们生活所处环境越来越复杂，不确定性因素逐渐增加。q-阶正交模糊集涵盖了直觉模糊集、Pythagorean模糊集，相对于直觉模糊集和Pythagorean模糊集而言，q-阶正交模糊集的约束条件更宽，决策者具有更为灵活的应用空间，信息失误范围会更小，q-阶正交模糊集能够更好地诠释人们对客观不确定性事物描述的惯性思维。目前q-阶正交模糊集被应用于供应链、风险投资、模式识别等领域，同时，其也成为了决策领域的一个重点研究方向。

由于q-阶正交区间模糊变量[7]可以更客观、更准确地表达客观世界的不确定性和模糊性，因此，本文在q-阶正交区间模糊集和文献[21]的基础上，研究了q-阶正交区间模糊环境下的Einstein信息算子的应用问题，并将其应用到高校教育教学优劣评估的多属性决策的问题中，同时验证了所提方法的实用性和正确性。

1 预备知识

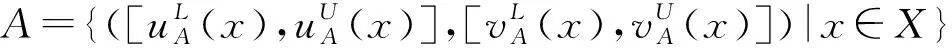
(1)

αj的精确值函数H(αj)定义为

(2)

定义3[13]令α1和α2为任意两个q-阶正交区间模糊变量，则q-阶正交区间模糊变量的排序方法可定义如下:

1) 如果E(α1)>E(α2)，那么，α1>α2;

2) 如果E(α1)=E(α2)，那么，若H(α1)>H(α2),则α1>α2;若H(α1)=H(α2)，则α1=α2。

定义4[16]Enistein T模和S模的表达形式如下:

式中:x,y∈[0,1]。

2 q-阶正交区间模糊环境下Enistein信息集成算子的运算规则

根据q-阶正交区间模糊变量和Enistein T模和S模的定义，下面定义了q-阶正交区间模糊环境下Enistein信息集成算子的运算规则。

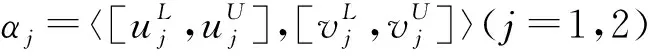
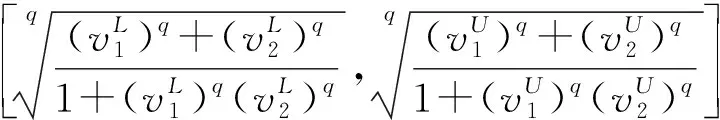
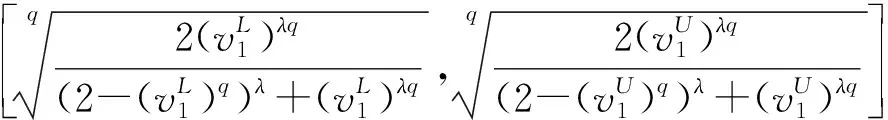
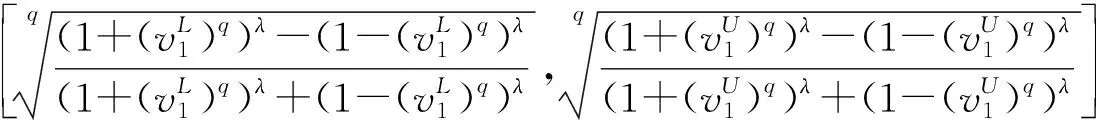
容易证明上述几种计算结果仍为q-阶正交区间模糊变量。

定义6设αi和αj为两个q-阶正交区间模糊变量，k,ki,kj≥0，则有如下运算规则:

1)αi⊕αj=αj⊕αi；2)αi⊗αj=αj⊗αi；3)k(αi⊕αj)=kαi⊕kαj；4) (ki⊕kj)αi=kiαi⊕kjαi；

结论易证，此处省略。

3 q-阶正交区间模糊Enistein信息集成算子

根据q-阶正交区间模糊Enistein信息集成算子的运算规则，下面定义两种q-阶正交区间模糊Enistein信息集成算子。

定义7设αj(j=1,2,…,n)是一组q-阶正交区间模糊变量，则q-阶正交区间模糊Enistein加权算术平均(q-Rung Interval-Valued Orthopair Fuzzy Einstein Weighted Average,q-RIVOFEWA)算子可定义如下，且有

q-RIVOFEWA:Ωn→Ω，

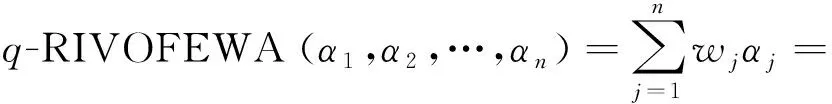
(3)

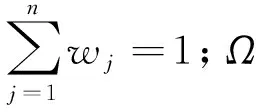
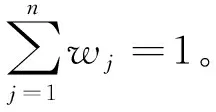
q-RIVOFEWA(α1,α2,…,αn)=a。

证明比较容易，略。

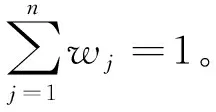
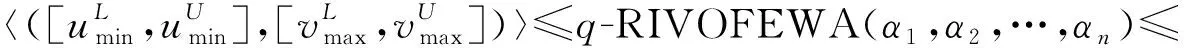
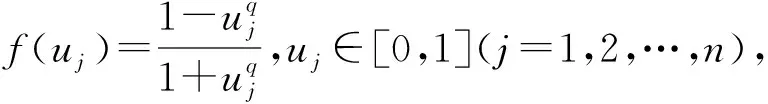
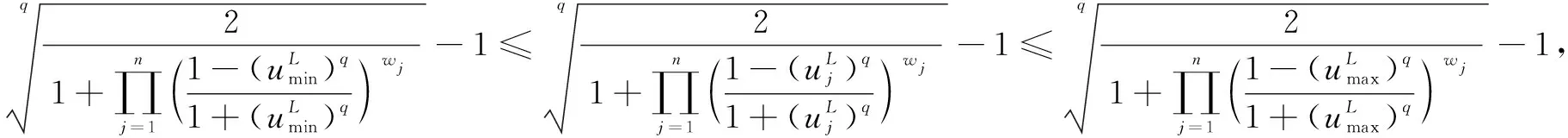
则有

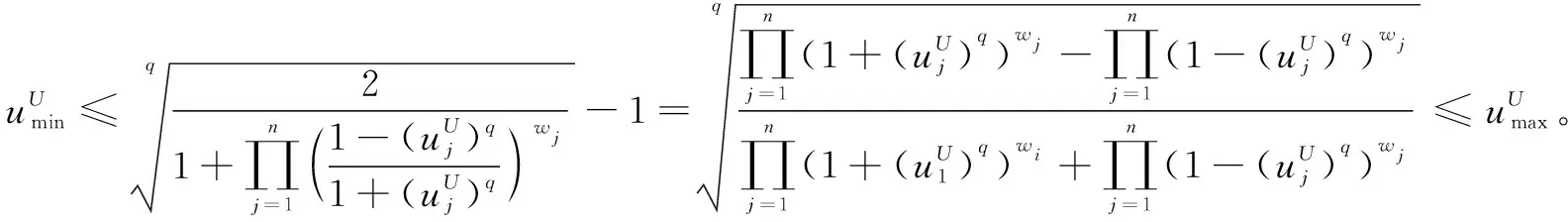
即有

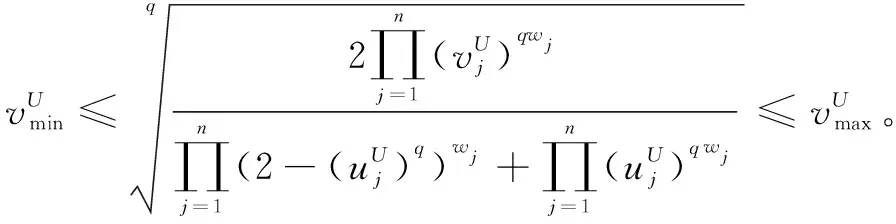
根据定义2和定义3可得

证毕。

定理3(单调性)设αj，α′j(j=1,2,…,n)是两组q-阶正交区间模糊变量，对所有的j，均有αj≤α′j，那么

q-RIVOFEWA(α1,α2,…,αn)≤q-RIVOFEWA(α′1,α′2,…,α′n)。

与有界性证明类似，此处省略。

定义8设αj(j=1,2,…,n)是一组q-阶正交区间模糊变量，那么q-阶正交区间模糊Enistein加权几何平均(q-Rung Interval-Valued Orthopair Fuzzy Einstein Weighted Geometry,q-RIVOFEWG)算子可定义如下，且有

q-RIVOFEWG:Ωn→Ω，

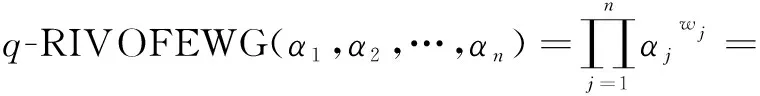
(4)

显然，与q-阶正交区间模糊Enistein加权算术平均算子(q-RIVOFEWA)类似，q-阶正交区间模糊Enistein加权几何平均算子(q-RIVOFEWG)也同样具有界性、幂等性、单调性等性质。

有时虽然获得了属性的位置权重，但却很难获得其权重信息，上述集成算子无法解决这种问题。针对此种情形，我们定义了有序加权信息集成算子。

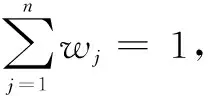
q-RIVOFEOWA:Ωn→Ω，

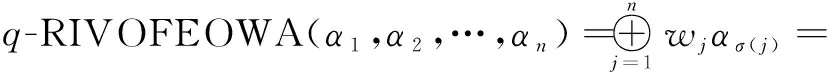
式中:sσ(j)为sj(s=u,v;j=1,2,…,n)中第j大的元素；Ω为所有q-阶正交区间模糊变量的集合。

与q-阶正交区间模糊Enistein加权算术平均(q-RIVOFEWA)算子类似，q-阶正交区间模糊Enistein有序加权算术平均(q-RIVOFEWA)算子同样具有界性、幂等性、单调性等性质。

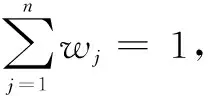
q-RIVOFEOWG:Ωn→Ω，

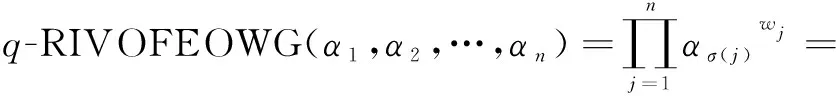
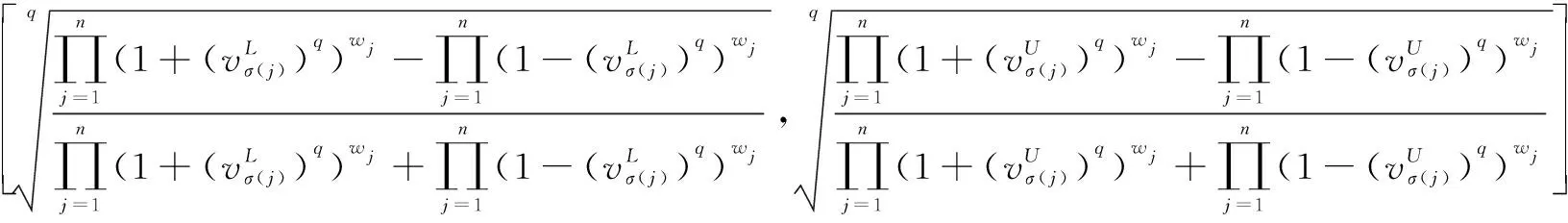
式中:sσ(j)为sj(s=u,v;j=1,2,…,n)中第j大的元素；Ω为所有q-阶正交区间模糊变量的集合。

4 q-阶正交区间模糊Enistein集成算子在决策中的应用

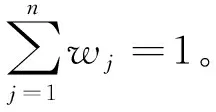
步骤1 运用q-阶正交区间模糊Enistein加权算术平均算子(q-RIVOFEWA)或q-阶正交区间模糊Enistein加权几何平均算子(q-RIVOFEWG)对R=[αij]m×n中的第i行进行集成，并求方案Ai的属性值αi:

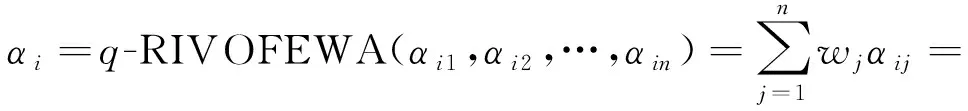
或

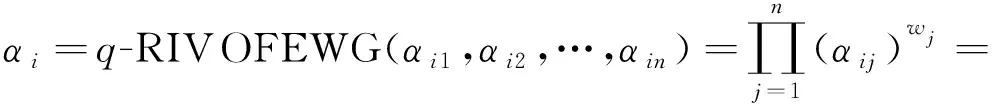
步骤2 计算Ai(i=1,2,…,m)方案的期望函数E(Ai)，若出现E(Ai)=E(Ai′)(i≠i′)，根据定义2，则需要进一步计算Ai(i=1,2,…,m)方案的精确函数H(Ai)(i=1,2,…,m)。

步骤3 根据定义3，选出最佳方案。

由于q-阶正交区间模糊集比直觉模糊集和Pythagorean模糊集应用范围更广，而Enistein T模和S模不仅可以进行运算，而且比代数运算更灵活，效果更好，本节基于q-阶正交区间模糊集和Enistein算子，提出了基于q-阶正交区间模糊Enistein加权算术平均算子和q-阶正交区间模糊Enistein加权几何平均算子的两种多属性决策方法，这两种方法可以处理更复杂的信息，专家或决策者可以根据自身的兴趣和实际需求，来选择适当的q的值,在应用上具有一定的方便性和灵活性。

5 示 例

某教育部门对当地的4个学校{A1,A2,A3,A4}进行教学评估，从以下方面进行考核: 教学运行与监控C1；教育质量与成果C2；专业建设C3；社会评价C4。这4个方面的属性权重为w=(0.25,0.30,0.30,0.15)。专家运用q-阶正交区间模糊集给出各个学校的评价值R=[αij]m×n，见表1。请根据评估结果对上述4个学校进行优劣排序。

表1 4个学校的评价值

下面研究当q=3时4个学校的优劣排序情况。

方法1 运用q-RIVOFEWA算子。

步骤1 根据式(5)，利用q-RIVOFEWA算子对矩阵R=[αij]m×n中的第i行进行集成，得到Ai的属性值αi。

步骤2 由定义2可以计算出αi的期望值:

E(α1)=0.445,E(α2)=0.373,E(α3)=0.343,E(α4)=0.420。

步骤3 根据定义3,对方案Ai(i=1,2,3,4)进行排序，其中得分函数s(Ai)=E(αi)，得A1≻A4≻A2≻A3，可知A1为最佳选择方案。

方法2 运用q-RIVOFEWG算子，得出的结论和方法1相同，此处省略。

我们通过分别改变q-RIVOFEWA算子和q-RIVOFEWG算子中q的值来描述参数对排序结果的影响，见表2和表3。

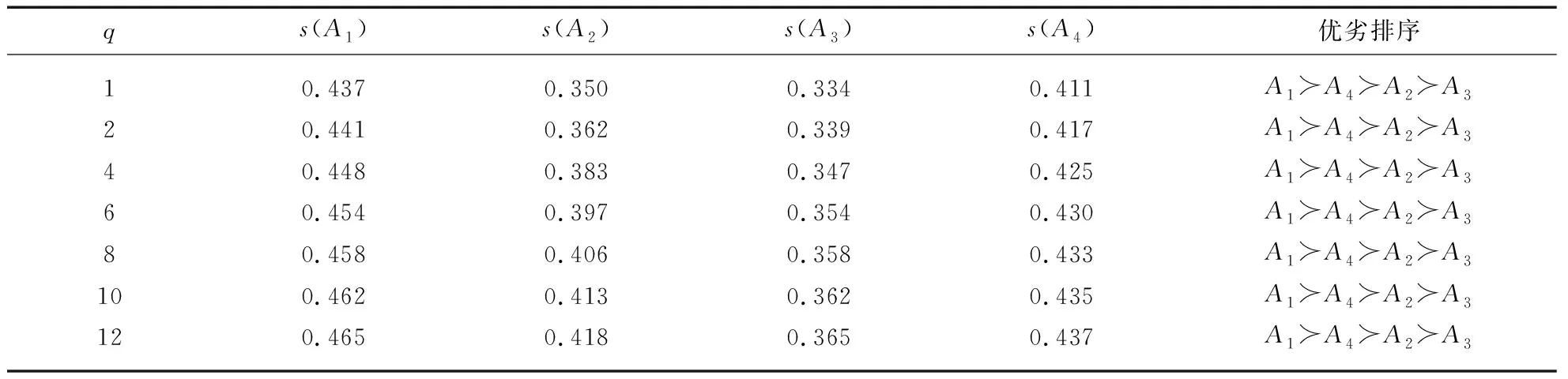
表2 根据不同的q值运用q-RIVOFEWA算子对方案Ai进行优劣排序

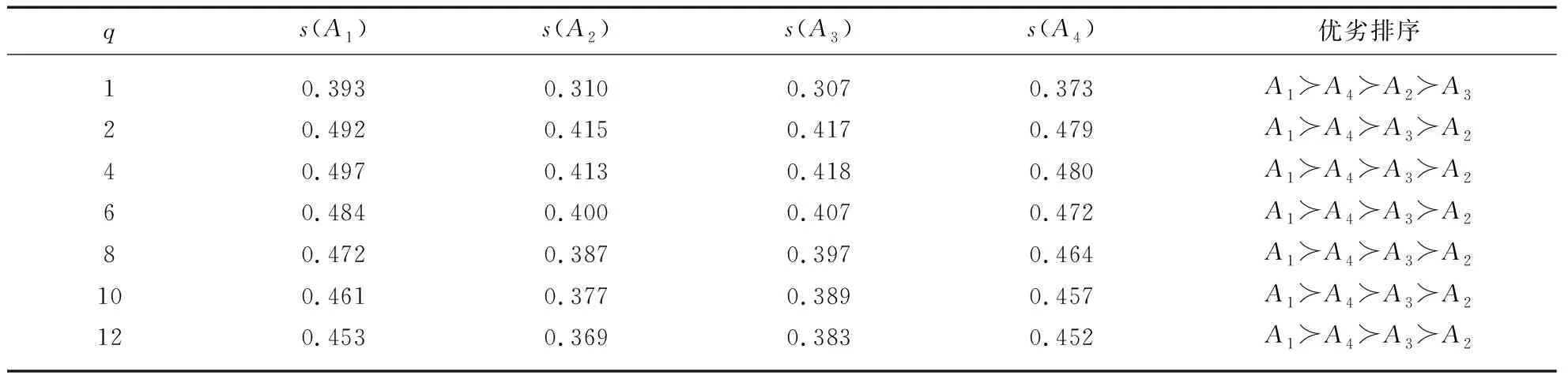
表3 根据不同的q值运用q-RIVOFEWG算子对方案Ai进行优劣排序

由表2和表3可知，基于q-RIVOFEWA算子和q-RIVOFEWG算子的群决策方法，随着q由1增加到12，示例中显示的排序结果趋于稳定，用两种不同的决策方法得出的最终结果是一致的，A1的评估分数最高，即A1为最佳选择方案。

为了更好地阐述文中所提方法的正确性和实用性，下面分别运用现有的几种决策方法对示例进行求解:

1) 基于区间直觉模糊加权算术平均(Interval-Valued Intuitionistic Fuzzy Weighted Average, IVIFWA)算子和区间直觉模糊加权几何平均(Interval-Valued Intuitionistic Fuzzy Weighted Geometry, IVIFWG)算子[22]的群决策方法进行计算，所得结果如表4所示。

表4 基于IVIFWA算子和IVIFWG算子的决策方法求解的结果

2) 运用优劣解距离(Technique for Order Preference by Similarity to an Ideal Solution, TOPSIS)方法[23]，对上述例题求其贴进度，可求得上述多属性群决策问题的优劣排序为A1≻A4≻A2≻A3，即A1为最优方案。

从排序结果来分析，基于IVIFWA算子和IVIFWG算子的方法与运用TOPSIS方法所得的结论一致，即A1为最优方案。这与我们基于q-RIVOFEWA算子的评价方法和基于q-RIVOFEWG算子的评价方法的结论相同。

通过与其他两种方法的比较，本文提出的决策方法具有以下的优点:

1) 第1种方法运用区间直觉模糊集来处理决策问题，由于此模糊集具有一定的局限性，无法解决隶属度与非隶属度之和大于1的情形，本文运用的q-阶正交区间模糊集是区间直觉模糊集的推广，能更好地处理此类问题，并且可以根据决策者偏好，适当选择q的取值来研究决策问题。

2) 第2种方法运用了TOPSIS方法，由于此方法在研究贴进度时有一定的缺陷性，最优解与负理想解的距离越远，越无法满足最优解靠近正理想解，而本文提出的方法可以有效避免上述问题。因此，本文所提方法更加优越，适用性更广。文中所提出的两种算子比区间直觉模糊算子和直觉模糊算子在应用上更具有一般性和普遍性，从而验证了文中所提方法的有效性和正确性。

6 结 语

本文在q-阶正交区间模糊集的基础上研究Enistein算子在多属性决策中的应用问题，此类研究在国内外尚处于起步阶段，本文的研究具有较大的理论价值和实际意义。

本文首先在q-阶正交区间模糊集和Enistein算子的基础上，定义了Enistein算子在q-阶正交区间模糊环境下的运算公式、期望函数、精确函数以及比较大小的规则；然后，定义了几种q-阶正交区间模糊Enistein信息集成算子，如q-阶正交区间模糊Enistein加权算术平均算子、q-阶正交区间模糊Enistein加权几何平均算子、q-阶正交区间模糊Enistein有序加权算术平均算子、q-阶正交区间模糊Enistein有序加权几何平均算子，并给出了算子具有的幂等性、单调性、有界性等性质；最后，将这些算子应用于属性权重确知且属性值以q-阶正交区间模糊变量形式给出的教育评估决策问题中。

本文有如下创新: 1) 将q-阶正交区间模糊集和Enistein算子相结合，提出了q-阶正交区间模糊Enistein算子的运算规则以及比较原则；2) 定义了两种q-阶正交区间模糊Enistein信息集成算子；3) 介绍了两种不同的方法来研究多属性群决策问题，本文提出的群决策方法可进一步运用到风险管理、最优化理论、供应链等领域。

致谢:感谢中国社会科学院大学2019年校级拔尖项目(20190027)、中国社会科学院大学2019年校级卓越项目(20190006)、中国社会科学院大学2020年重大专项项目(2020-KYLX01-06)对本研究的大力支持！