大数据岭回归的最优子抽样

陈云璐，张 楠

(复旦大学 大数据学院，上海 200433)

线性回归是一种用于描述响应变量y∈Y⊂与协变量x∈X⊂p关系的经典方法。对于n个独立同分布数据考虑线性模型其中：εi是均值为0、方差为σ2的独立同分布误差项。模型可以写成如下的矩阵形式:

y=Xβ+ε。

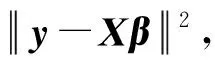
岭回归[1]于1970年被初次提出，最初用于解决计算最小二乘估计时X病态的问题。岭回归估计定义为

(1)

式中:λ>0，它被称作岭参数。岭回归估计的优化函数可以写成

(2)

惩罚项给估计带来了偏差，但同时也降低了方差，我们可以通过调节岭参数λ达到偏差与方差的权衡[2-3]，常用的方法为交叉验证(Cross Validation, CV)和广义交叉验证(Generalized Cross Validation, GCV)[4]。

在海量数据上做估计往往会受到计算能力的限制，因此如何在大矩阵上处理计算问题成为了近年的研究热点，不同领域学者从矩阵低秩估计[5-6]、机器学习算法的coreset研究[7-8]、sketching[9-11]等各角度提出了相应的方法。具体到岭回归这一问题中，研究者关注到了岭杠杆值这一变量，即矩阵X(XTX+λI)-1XT的对角元素[12]，并在近年的研究中将它拓展使用于低秩投影方法中[13]。此外，有学者对压缩矩阵是稀疏伯努利形式时的特殊岭回归估计问题进行研究，得到了子样本估计的偏差和方差[14]。

子抽样可被视作随机投影或sketching的一种特殊情形，其一般步骤是: 从原始数据中依照某种抽样准则来选取相应的子样本后，使用该子样本进行估计。根据抽样的准则可以将现有研究大致分为决定性方法和随机性方法两类。决定性方法是指当原始观测及子数据的数据量确定的时候，重复这一类方法得到的子样本也是确定的，在计算子样本估计量的方差时，这种确定性具有特定优势。例如，Wang等[15]提出对设计矩阵的每个维度选择拥有极端值的观测数据作为最优子数据，该最优性旨在使选出的子样本能够使得其信息矩阵的行列式的界被控制。随机性方法是指给定选中每个数据的概率进行抽取，其优点在于方法的鲁棒性更强，不易受到离群值的影响。比如在大样本线性回归问题中，Drineas等[16]和Ma等[17-18]提出了使用杠杆值相关的量(杠杆值指X(XTX)-1XT的对角线元素)进行随机性子抽样。此外，在逻辑回归[19]、分位数回归[19]及广义回归[21]的框架下均有相应的随机性子抽样方法的研究。

本文旨在减轻大数据岭回归的计算负担，即考虑样本量n远大于维度p的情况。Ma等[17-18]在研究普通线性回归子抽样问题的工作中，以子样本估计的渐近结果为出发点，得到了线性回归下的最优子抽样概率。受其启发，我们研究了基于子样本的岭回归估计的渐近偏差与方差，并使用渐近均方误差作为抽样概率选取的优化准则，以期达到偏差与方差的权衡。通过计算，我们可以得到最优子抽样概率，其与岭杠杆值及协变量的L2范数均有关。大部分现有的子抽样方法基于回归框架，并不考虑惩罚项，而在岭回归子抽样问题中我们需额外考虑如何选择恰当的岭参数。由于大样本计算的时间空间资源限制，我们很难直接在大数据整体上去计算岭参数和岭杠杆值。作为替代，对于岭参数的计算，我们选择使用在规模较小的子样本上进行交叉验证的方法。进一步地，对于每个岭杠杆值，我们用其均值近似地替代其本身，这样得到的最优子抽样概率正比于样本的L2范数。我们将在理论部分阐述这两点调整的合理性，并在仿真及真实数据上进行实验结果的展示。

1 研究方法

1.1 子抽样框架

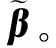
(3)

在上述的基本步骤中仍有两个问题需要解决:

我们将在后续的子章节中回答这两个问题。

1.2 岭参数的选择

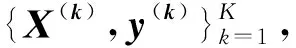
使用原始样本的不同部分进行重复拟合的过程会导致很高的计算成本，尤其是在样本量很大的情况下。广义交叉验证[4]被提出来以期降低交叉验证的计算成本，其主要思想如下: 考虑留一交叉验证(Leave-One-Out Cross-Validation, LOOCV)，即取K=n，

(4)

1.3 最优子抽样

当岭参数给定时，我们可以对每个观测计算子抽样概率，而后以这个概率从总样本中有放回地抽取子样本，我们期望这个基于子样本的估计能达到一定的最优性。在偏差和方差权衡恰当时，岭回归估计能比最小二乘估计表现得更好，因此我们考虑一个形式上同时包含偏差和方差的优化目标，即均方误差。

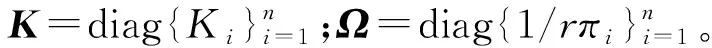
(5)

在下面的引理中，我们给出了估计式(4)与全样本估计式(1)之间的差值的近似。

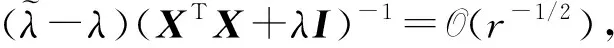
(6)

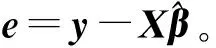
证 通过对式(5)右边乘I=(XTX+λI)(XTX+λI)-1，我们可以把子样本估计重新写成

(7)

对式(7)右边的逆项部分使用泰勒展开，得

对另一部分，有

(XTX+λI)-1XTWy=(XTX+λI)-1{XTy+XT(W-I)y}=

由于(XTX+λI)-1XT(W-I)y，(XTX+λI)-1XT(W-I)e与(XTX+λI)-1XT(W-I)X同阶，因此

(8)

第2个等号成立基于岭回归的正规方程。□

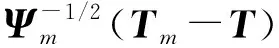
EAMS(Tm)=E(ZTΨmZ)=

tr(DA(Tm))+(EA(Tm)-T)T(EA(Tm)-T)。

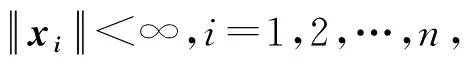
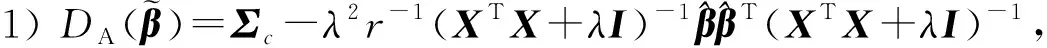
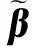
的迹。

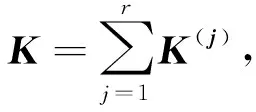
式中:D(x)表示方差；a=(XTX+λI)-1b。而通过岭回归的正规方程，我们可以将这一方差写成

然后，使用Lindeberg-Lévy中心极限定理，可得总和的方差同样为

由Cramer-Wold定理即可得到结论1)。

(9)

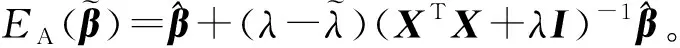
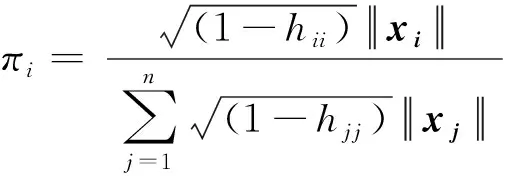
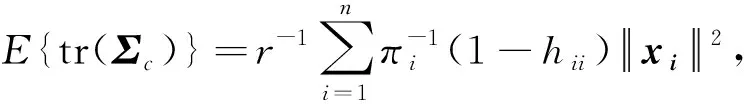
定理2得到了每个观测的最优子抽样概率，它与岭杠杆值及L2范数有关。值得注意的是，我们的子抽样方法与从sketching角度出发的岭杠杆值抽样方法[13]相关但又不同，后者只与岭杠杆值有关，在后续的仿真与真实数据上，我们将比较它们的表现。

2 算 法

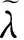
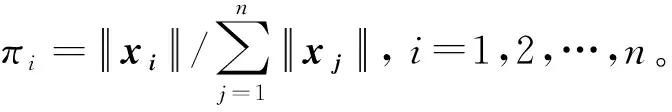
算法1基于最优子抽样的岭回归估计

步骤2 使用子样本计算岭回归估计,

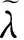
相比于精确计算岭杠杆值，这一算法避免了直接对大规模矩阵X进行处理，因此在实际操作中可以进一步去并行计算L2范数来降低计算时间。在仿真实验中，我们将算法1的结果和使用精确岭杠杆值的抽样算法进行比较，从而说明岭杠杆值近似的有效性。

3 仿真数据实验

在仿真数据上，我们首先比较使用精确岭杠杆值和近似岭杠杆值抽样的结果，然后将新方法与其他大数据岭回归子抽样方法及线性回归子抽样方法进行比较，其中用于比较的大数据岭回归子抽样方法是岭杠杆值抽样[13]和均匀抽样，线性回归子抽样方法是最优子抽样[18]和基于信息的子样本选择方法[15]。

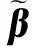
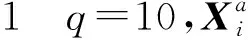
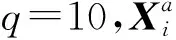
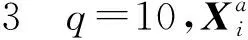
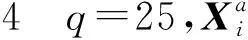
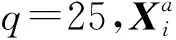
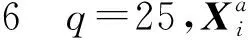
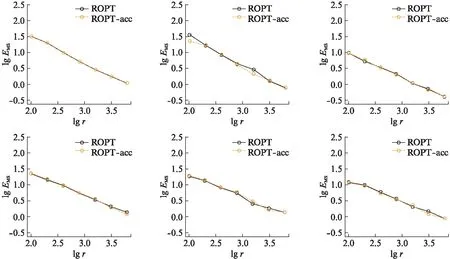
图1 仿真1—6上，新方法与使用精确岭杠杆值方法的对数均方误差Fig.1 Logarithm of MSE comparison of our algorithm and accurate ridge leverage score subsampling on simulation 1—6

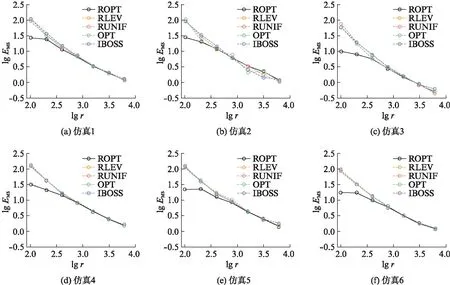
图2 仿真1—6上，不同子抽样方法的对数均方误差Fig.2 Logarithm of MSE comparison of different subsampling estimators on simulation 1—6

4 实际数据实验

本节我们关注网络新闻数据的流行度预测，并采用相应的实际数据进行子抽样回归实验。在当今这一信息爆炸的时代，人们在互联网上昼夜不停地被各种不同来源的新闻所轰炸，对于线上媒体而言了解哪种新闻能够引起公众的关注至关重要，因此对新闻流行度的预测成为了一个热门的研究话题。为了提升预测的准确性，新闻内容、关键字、发布日期等多类特征被提取出来后放入回归模型中以进行新闻转发数的预测。在本章中，我们使用的是UC Irvine提供的公开机器学习网络新闻流行度数据集(Online News Popularity Data Set)(http:∥archive.ics.uci.edu/ml/datasets/Online+News+Popularity)。

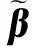
图3所示为通过不同方法计算出的估计量的均方误差。在子样本量比较小的情况下，新方法已经有了较大的优势，换言之，对这一实际数据，新方法能在提升计算效率的同时达到比较好的估计效果。可以看到，此时另4个竞争方法中，线性回归最优子抽样(OPT)方法和岭回归下的均匀抽样(RUNIF)方法相对表现较好，而新方法相当于结合了这两种方法在抽样概率计算及惩罚项引入上的优势。在子样本量较大时，新方法的表现依旧最优，线性回归下基于信息的子样本选择(IBOSS)方法次之，尽管IBOSS方法在子样本量为1 600和3 200时一度接近新方法，但该方法本身在不同大小的子样本下的表现差距很大。这是由于它是一种决定性方法，容易受离群值的影响，而新方法作为随机性方法则更为鲁棒，因此在不同子样本量下新方法保持了其优势。

图3 实际数据上，不同子抽样方法的 对数均方误差Fig.3 Logarithm of MSE comparison of different subsampling estimators on real data

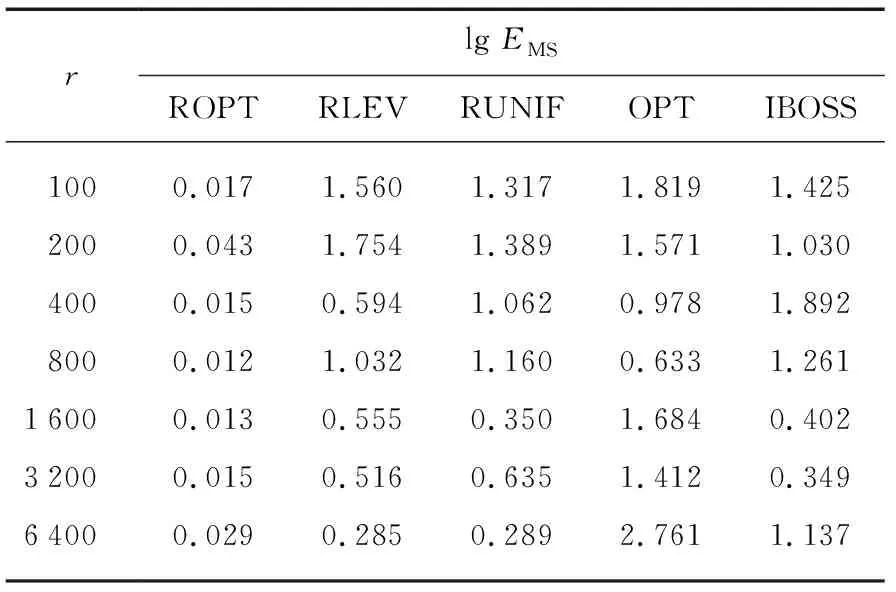
表1 不同子样本量下的对数测试集误差比较

在不同子样本量下，新方法的表现相较于各竞争方法始终更优。此外，通过比较岭回归下的均匀抽样方法和线性回归最优子抽样方法在子样本量较大时的表现，我们发现惩罚项的引入在控制测试集误差上起到了一定的作用。相较于子样本估计与全样本估计的均方误差，测试集误差能够更好地比较各个方法，原因在于全样本估计和模型真实参数可能存在偏差。然而在实际数据上我们无法确知真实参数，所有样本构成了我们可以得到的全信息。测试集误差最小说明了新方法不仅较好地接近全样本估计，而且也比较接近真实模型的情形。