双向EDFA在长距离分布式光纤传感系统中的级联方案

韩纪磊，肖 倩，陈永超，周鹏威

(复旦大学 材料科学系，上海 200433)

在一些长距离光纤传感系统中，如基于Sagnac或Michelson结构的分布式光纤传感系统，为了满足光纤中双向光传输的需要，经常需要利用双向掺铒光纤放大器(Erbium-doped Fiber Amplifier, EDFA)来实现双向光放大、抵抗光损耗等，但双向EDFA的引入会导致系统不可避免地产生一系列噪声，这些噪声会在放大信号中产生光起伏，当噪声与被放大的信号光一同进入光电探测器后，光起伏在光电探测器中会引起电起伏，产生光电流噪声，对光电探测器光电流噪声的主要贡献来源于自发辐射与信号光的拍频噪声[1]。而通过合理的控制EDFA的输入光功率，可使拍频噪声对系统的影响保持在较低水平[ 2]。在实际应用中发现，光纤传感系统的性能随EDFA的信号光功率与泵浦电流变化。本文从基于Giles-Emmanuel模型的EDFA速率方程和功率传输方程出发，理论上分析了信号光功率与泵浦电流对光纤传感系统性能的影响。并设计了长距离光纤传感系统中的传感光路，分析了EDFA信号光、泵浦电流、信号光带宽等因素对光纤传感系统性能的影响。并在实验基础上提出了双向EDFA独立恒量控制法，可以使系统在已有放大器工作状态不受影响的基础上，级联新的传感光纤和双向EDFA，并通过实验验证了这一方法的有效性。

1 理论方法

在不考虑激发态吸收，也就是泵浦光源在980 nm或1 480 nm泵浦带的情况下，可以将EDFA等效为二能级系统，由于亚稳态能级和基态能级具有一定宽度，因此EDFA的增益谱具有一定的波长范围[3-8]。

亚稳态能级的粒子数密度满足如下速率方程

(1)

功率传输方程满足

(2)

式中：

(3)

(4)

因此，随着泵浦光功率Pp(z)的增加，亚稳态能级的粒子数浓度也逐渐增加，直至粒子数达到完全反转。

当掺铒光纤中处于亚稳态能级的粒子数浓度保持平衡状态时，EDFA中的信号光功率，泵浦光功率以及自发辐射光功率满足式(2)，将式(2)拆分成下面3个方程：

(5)

(6)

(7)

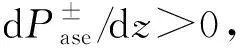
保持输入EDFA的信号光功率不变，增加EDFA的泵浦光功率，经过EDFA输出的信号光功率以及信号光功率占EDFA总的输出光功率的比例也随泵浦光功率变化，利用式(5)、(6)、(7)得

(8)

2 实 验

采用干涉型光纤传感器研究EDFA的工作特性，搭建的单芯反馈式干涉结构如图1所示。

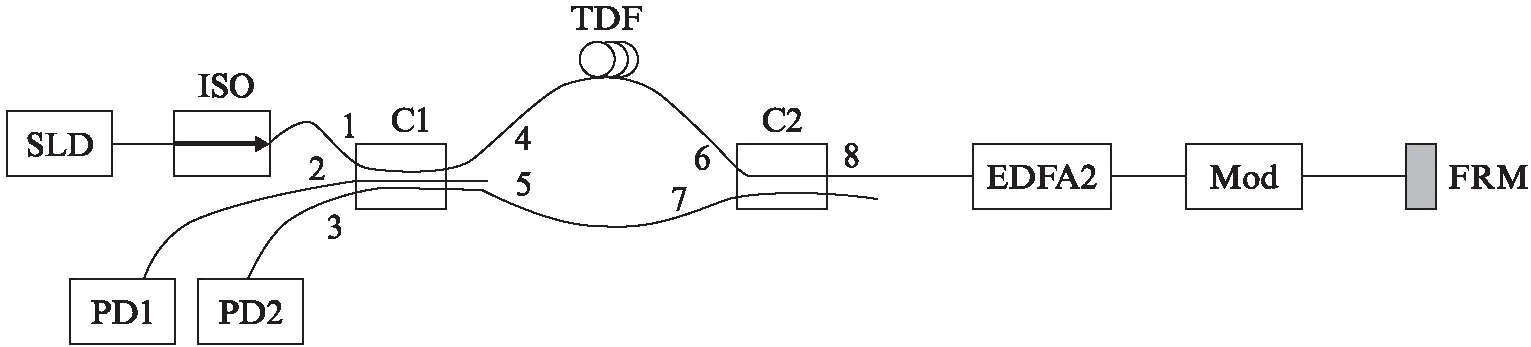
图1 研究EDFA工作特性的实验结构Fig.1 Experimental structure for studying the working characteristics of EDFA

图1中： SLD是中心波长1 550 nm，半高全宽大于等于35 nm的宽谱光源；ISO为隔离器；PD1，PD2为光电探测器；C1，C2为构成干涉结构的均分型光学耦合器；TDF为光纤延迟线；Mod为相位调制器；FRM为法拉第旋转镜。该干涉系统存在着两束光程相等的路径，分别为：

Path1： 1→4→TDF→6→8→EDFA2→Mod→FRM→Mod→EDFA2→8→7→5→C1；

Path2： 1→5→7→8→EDFA2→Mod→FRM→Mod→EDFA2→8→6→TDF→4→C1。

这两路信号光经过相位调制器后产生随时间变化的相位差，设到达耦合器C1处时，两路光的相位差为φ0+φM，其中：φ0为由耦合器产生的初始相位差，φM为相位调制器产生的相位差。两路信号光在C1处发生干涉，干涉信号的大小为

(9)

在本实验中，调整双向EDFA2的正向输入光和输出光，利用衰减器，在Mod不加载信号的情况下，控制每次进入探测器PD1的光功率恒为1 μW，该光功率中除了参与干涉的光信号，还包含未发生干涉的自发辐射噪声等。Mod加载信号时，通过分析干涉信号的幅值，可得知不同条件下，信号光功率占EDFA2的总的输出光功率的比例[9-11]。干涉信号幅值越大，代表EDFA2输出的信号光功率占总输出光功率的比例越大，即代表着EDFA2在这种工作状态下的性能越强。

由于泵浦电流与信号光功率以及信号光带宽等会影响双向EDFA的工作性能，因此，实验测试了宽谱信号光0 km，窄谱信号光0 km，窄谱信号光50 km这3种情况下双向EDFA工作性能的差异，实验结构分别如图1、图2和图3所示。

图2 窄谱信号光条件下研究EDFA工作性能的实验结构Fig.2 Experimental structure for studying the characteristics of EDFA under narrow-spectrum signal light

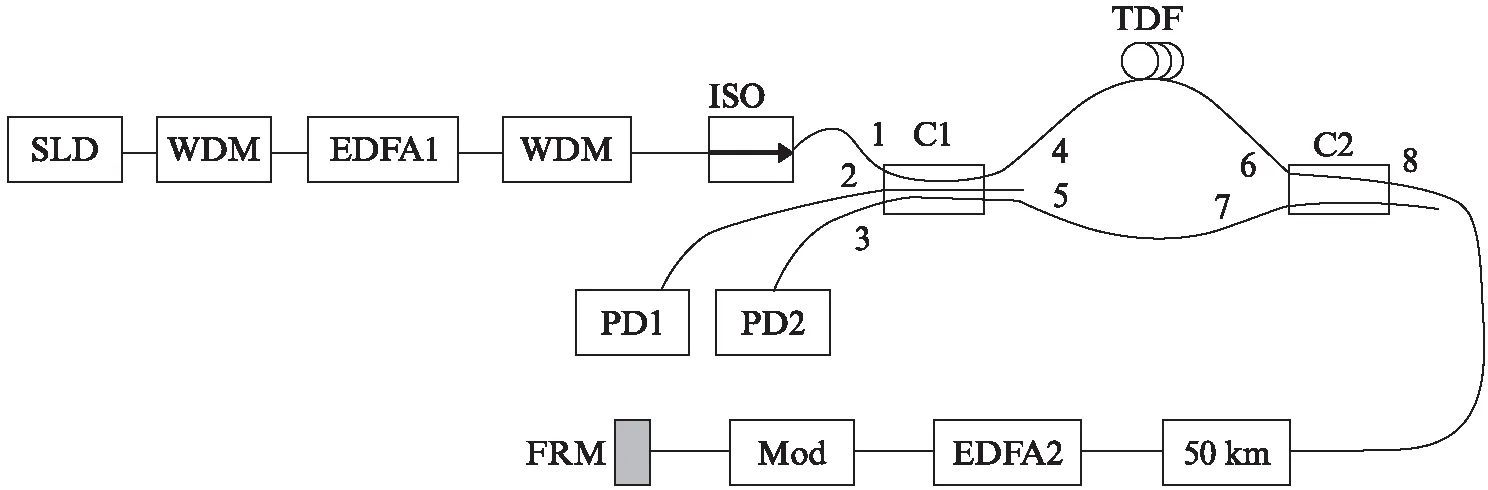
图3 传感距离为50 km时研究EDFA工作性能的实验结构Fig.3 Experimental structure for studying EDFA performance at a sensing distance of 50 km

与图1相比，图2所示结构在宽谱光源SLD与光隔离器之间增加了WDM-EDFA1-WDM，用来控制输入干涉系统的信号光带宽，探究信号光带宽对EDFA工作性能的影响，WDM是中心波长为1 553.3 nm，带宽为1.6 nm的波分复用器。与图2相比，图3所示结构在干涉模块与EDFA2之间增加了50 km单模光纤，用来探究传感距离为50 km时，双向EDFA的工作性能。

3 实验结果及讨论

3.1 泵浦电流对传感系统性能的影响

为研究双向EDFA的泵浦电流对传感系统性能的影响，采用图1所示的光路，控制每次进入探测器的光功率1 μw，测到干涉信号的峰峰值随信号光功率和泵浦电流的变化趋势如图4所示。从图4中可以看出，在同一信号光功率下，随着泵浦电流升高，干涉信号峰峰值先是迅速上升，随后达到最高，此时的泵浦电流为这一信号光下的最佳泵浦电流，继续增加泵浦电流，峰峰值逐渐下降，这种变化趋势，与前面公式推导出的结论相一致。说明随着泵浦电流升高，掺铒光纤中总的反转粒子数增多，但用于受激辐射的反转粒子数的比例先升高(反转粒子数主要用于放大信号光)后降低；最佳泵浦处，用于受激辐射的反转粒子数的比例达到最大，用于自发辐射的反转粒子数的比例达到最小；从图中可以看出随着双向EDFA输入光功率的增加，最佳泵浦电流基本在上升或者保持不变；继续增加泵浦电流，信号光不足以激发大量的高能态粒子跃迁，此时EDFA的增益也趋于稳定，用于自发辐射的反转粒子数比例开始增加，导致系统噪声增加，性能降低。因此，在某一确定输入光功率下，调节EDFA的泵浦电流至最佳泵浦电流处，会使系统整体的工作性能处于最佳状态。

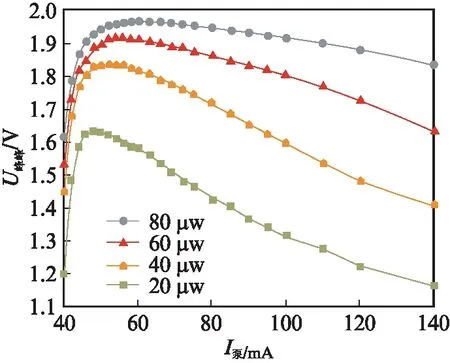
图4 泵浦电流对干涉信号峰峰值的影响Fig.4 Effect of pump current on peak-to-peak value of interference signal

3.2 信号光功率对传感系统性能的影响

图5描述的是在窄谱0 km的实验基础上，泵浦电流分别为42、46、60、80 mA时干涉信号峰峰值随信号光功率变化的情况。从图中可以看出，随信号光功率增加，干涉信号峰峰值也会增加，最后趋于平稳，说明信号光功率对双向EDFA具有积极影响。由于相同泵浦电流下，反转粒子数基本一致，当信号光逐渐增大，参与受激辐射的反转粒子数越多，自发辐射越弱，在EDFA的输出光功率中，信号光的占比就越多。因此在一定范围内，输入EDFA的信号光应该越大，能够使光纤传感系统的工作性能越好。但输入EDFA的信号光不能无限增大，当信号光增大到某一值后，反转粒子数浓度不足以继续增大信号光，随着信号光增加，放大倍数逐渐减小，同时，EDFA噪声指数逐渐增大[12]。因此，在每一个泵浦功率下都会有一个合适的输入光功率。

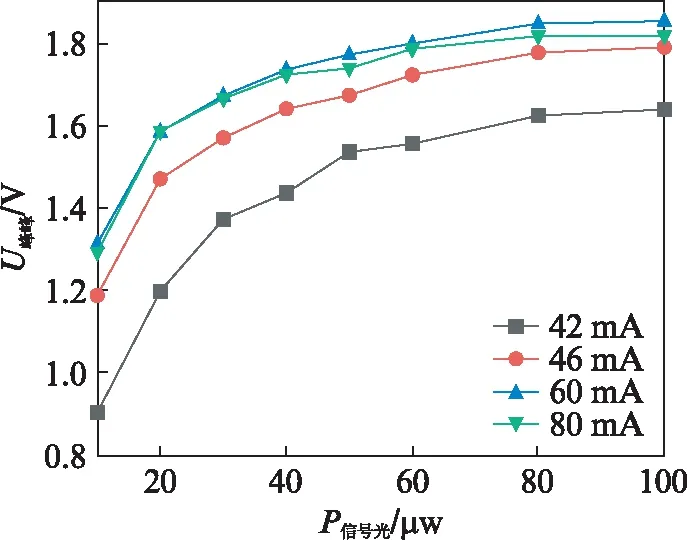
图5 放大器输入信号光功率对干涉系统性能的影响Fig.5 Effect of signal light power on phase holding performance of amplifier

3.3 信号光带宽对传感系统性能的影响

为了比较信号光带宽对EDFA工作性能的影响，对宽谱和窄谱条件下，不同输入信号光所得到的干涉信号峰峰值的最大值进行统计如图6所示。从图中可以看出，窄谱输入时信号最大值大于宽谱的情况，且随着输入光的增大，趋势更加明显。对SLD滤出特定波长范围的光，可以提高传感系统得到的干涉信号峰峰值，等效于增加了系统的信噪比，而且在相同的输入光功率下降低了所需的泵浦电流值。

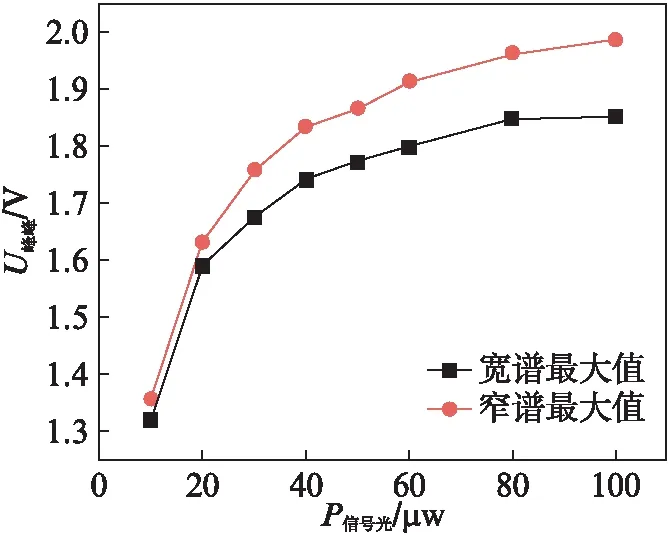
图6 干涉系统宽谱和窄谱输入下输出信号峰峰值Fig.6 The peak-to-peak value of the output signal of the inter- ferometric system under wide and narrow spectrum input

3.4 利用EDFA增加距离对传感系统性能的影响

利用图3所示的实验结构，测试了传感距离为50 km时，干涉信号峰峰值的变化。

图7为0 km和50 km两种距离下，信号光功率分别为60 μw和80 μw时的干涉信号峰峰值随泵浦电流的变化趋势图。可以看出，随着泵浦电流增加，0 km和50 km相应的曲线都是上升后下降，但50 km的干涉信号峰峰值有所下降，说明传感距离增加使整个干涉系统性能降低。

图7 传感距离为0 km和50 km时的比对图Fig.7 Comparison chart while the sensing distance is 0 km and 50 km

从图7中可以发现两种距离下，信号光为60 μw和80 μw时对应的最佳泵浦电流相同，分别为56 mA和60 mA，在所测得的所有10 μw到100 μw的数据中都存在这种现象，说明： EDFA位于传感路径的尾端时，最佳泵浦电流仅受进入EDFA的信号光功率影响。但是增加传感距离会导致系统效率的降低，这是因为传感距离的增加导致系统散射光比例的增加，从而导致信号光比例的减少，最终影响输出信号的峰峰值。

4 级联EDFA的优化方案

对双向EDFA进行级联会面临着不同双向EDFA之间相互影响以及系统调试难度大等问题。本文通过实验，设计了一种双向EDFA独立恒量控制法，能够在不影响系统已有的双向EDFA工作状态的情况下，增加传感距离和新的双向EDFA，有效减轻增加级联双向EDFA带来的的调试复杂度。该方法在光纤线路中引入一个大分光比的2×2光学耦合器，利用其获得独立的指标作为调节双向EDFA依据。详细工作方式如图8所示。

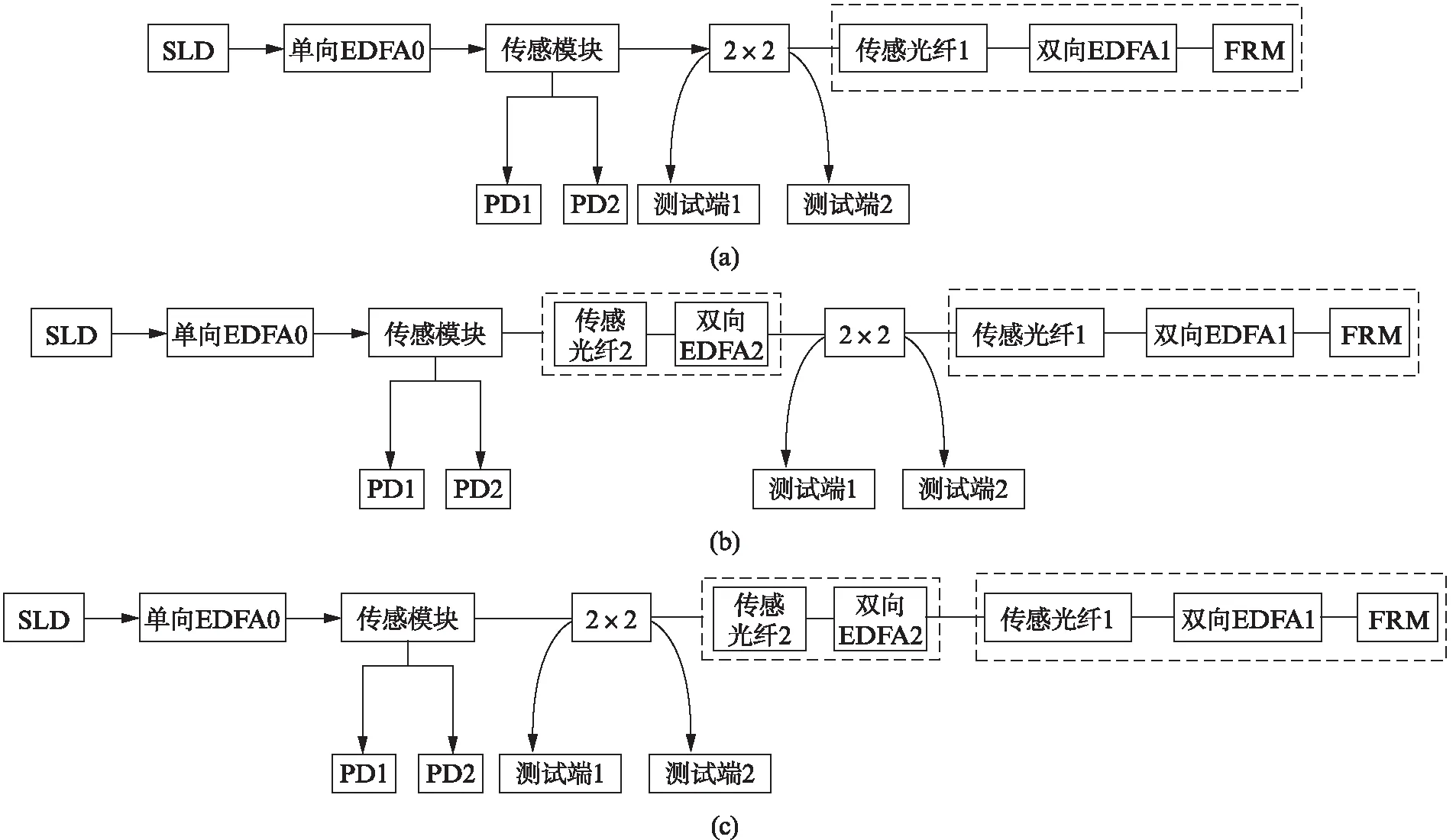
图8 级联EDFA的优化方案示意图Fig.8 Schematic diagram of the optimization scheme of cascade EDFA

如图8(a)所示，首先SLD经过单向EDFA0放大后经传感模块注入到99∶1的2×2大分光耦合器，输出光经传感光纤1进入双向EDFA1，2×2的两个1%的分光端测试端1和测试端2的输出可以作为独立指标，用于调节下一级双向EDFA的参考。首先调节单向EDFA0使到达双向EDFA1的光功率在其工作范围内，然后调节双向EDFA1使到达光电探测器PD1和PD2的光功率在其工作范围内。在一定的范围内变化EDFA0和EDFA1的参数，找到系统的最佳工作状态，记录下此时测试端1、2的光功率。

当扩展传感距离时，如图8(b)所示，在传感模块和耦合器之间加入传感光纤2和双向EDFA2.调节EDFA2，使测试端2的光功率与图8(a)状态时的光功率相同，则测试端1的光功率也相同。此时相当于把传感光纤1、EDFA1和FRM当做一个稳定的黑箱子，EDFA1的工作状态保持不变，而且黑箱子的输出光功率不变。

然后，把2×2耦合器移动到图8(c)中的位置，即传感模块和传感光纤2之间，测量测试端1和测试端2的光功率。由于2×2分光器分光比很小，上述移动对线路状态的影响可忽略不计。当继续添加传感光纤3和双向EDFA3时，把传感光纤2、EDFA2、传感光纤1、EDFA1和FRM当作一个稳定的黑盒子，重复以上状态调节步骤。从上述过程可以看出，该方法避免了双向EDFA之间工作状态的相互影响，保证系统始终处于最佳工作状态。

图9是测试端1和测试端2的光功率随双向EDFA级数增加产生的变化，实验中共测试了级联13级双向EDFA。从图9中可以看出： 测试端1的光功率随双向EDFA级数的增加而在不断的上升，这与实验中将2×2前移，散射光不断增加有关；测试端2的光功率随双向EDFA级数的增加基本不变，其光功率仅与EDFA0和传感模块后第一段光纤的损耗有关。

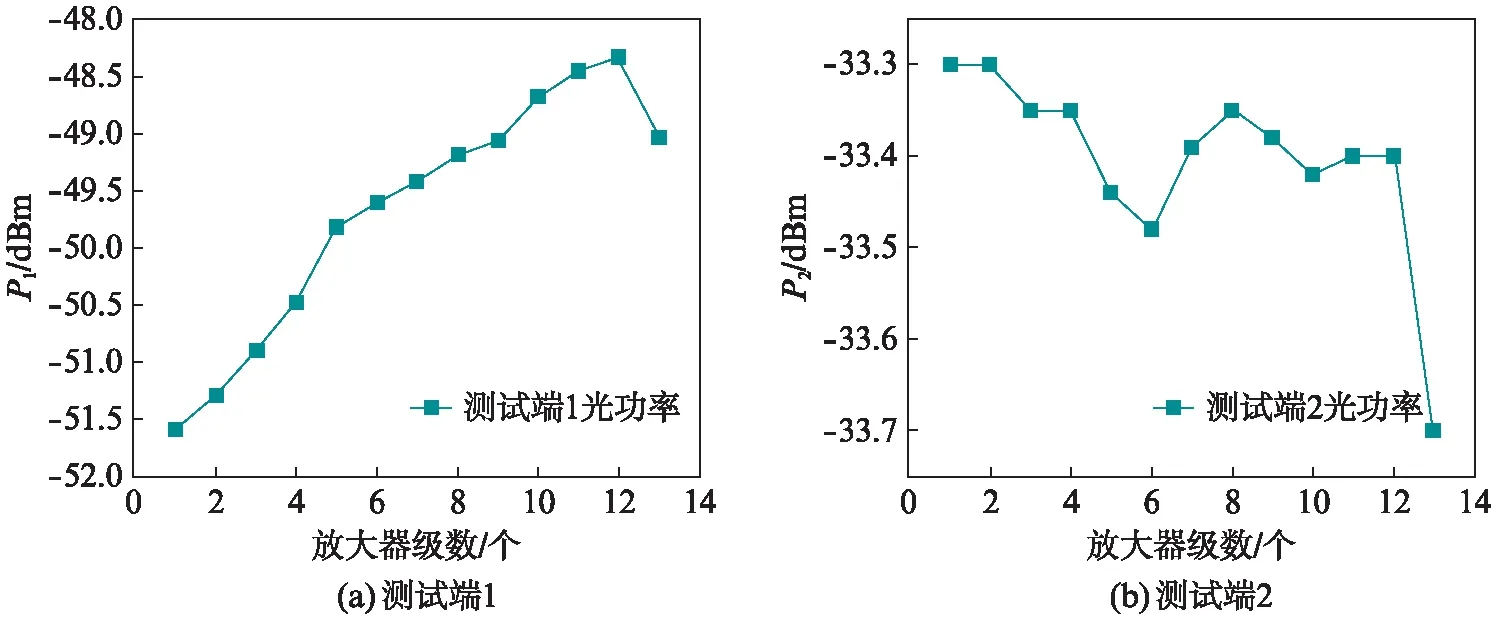
图9 测试端1、测试端2的光功率随双向EDFA级数的变化Fig.9 Changing of terminal 1 and terminal 2 with the bidirectional EDFA series

5 结 语

本文从EDFA的速率方程和功率传输方程出发，推导出EDFA的输出光中信号光占总输出光比例的变化公式，搭建了单芯反馈式干涉结构，分析信号光功率，泵浦电流，信号光带宽，以及传感距离对双向EDFA工作性能的影响。实验结果表明： 信号光功率一定时，存在最佳泵浦电流，使双向EDFA工作性能最佳；泵浦电流条件一定时，输入双向EDFA的信号光功率越大，干涉信号信噪比越高，但输入EDFA的信号光不能无限增大；窄谱信号光可以提升双向EDFA在最佳工作状态下的信噪比，同时，输入双向EDFA的光功率越大，窄谱信号光相比宽谱信号光工作效果越好。双向EDFA的级联易产生相互影响，破坏系统工作状态，利用本文提出的双向EDFA独立恒量控制法，可以方便地级联新的传感光纤和双向EDFA，使得各个双向EDFA均保持在最佳工作状态。通过双向EDFA独立恒量控制法测试了级联13级双向EDFA的状态，测试结果表明独立恒量控制法可以高质量的实现双向EDFA的级联。