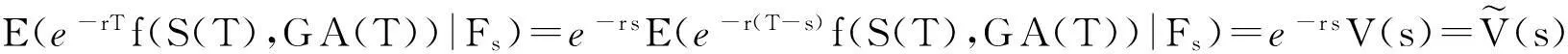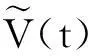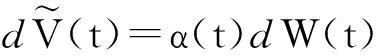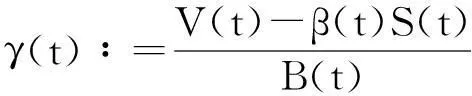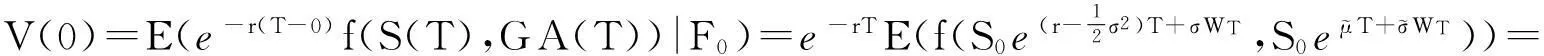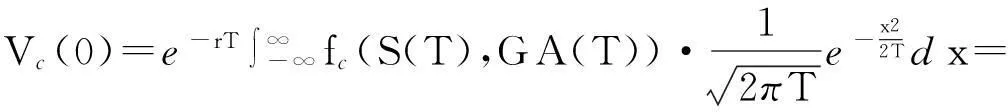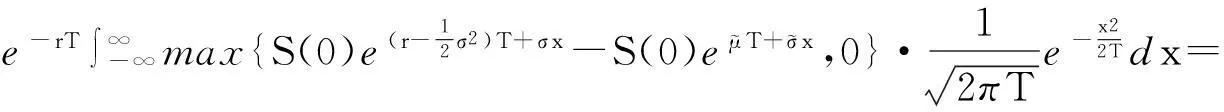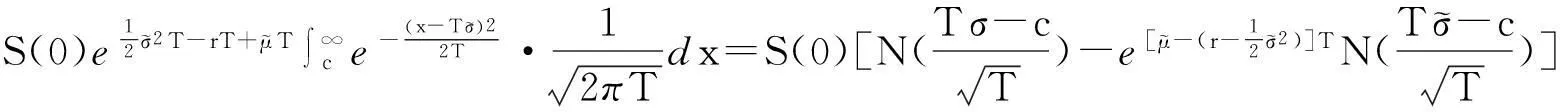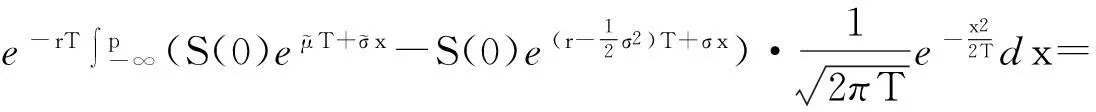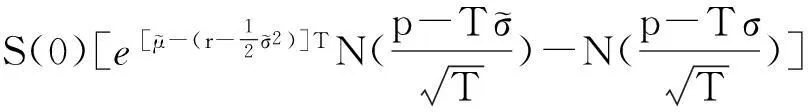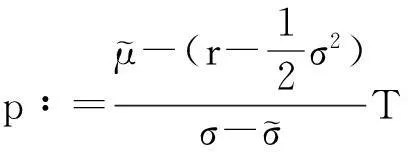基于离散几何平均的亚式期权定价研究
基于离散几何平均的亚式期权定价研究
洪义成1,金元峰1,李美善2
( 1.延边大学理学院 数学系,吉林 延吉 133002; 2.延边大学财务处,吉林 延吉 133002 )
摘要:讨论了离散情形下几何平均亚式期权的定价方法.首先对离散情形下的几何平均进行处理,然后利用标准欧式期权的定价公式得到了固定执行价格离散几何平均亚式期权的定价公式,最后利用鞅论的方法得到了浮动执行价格离散几何平均亚式期权的定价公式.
关键词:亚式期权; 几何平均; 期权定价
收稿日期:2015-07-03
作者简介:洪义成(1980—),男,理学博士,副教授,研究方向为金融统计学、保险精算学.
文章编号:1004-4353(2015)03-0199-04
中图分类号:F830.91
The method of pricing Asian options based on the discrete geometric average
HONG Yicheng1,JIN Yuanfeng1,LI Meishan2
( 1.DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China;
2.DepartmentofFinance,YanbianUniversity,Yanji133002,China)
Abstract:In this paper,we discussed pricing method of the geometric average Asian option in the discrete case. Firstly,we transform the geometric average into proper form,and then using Vanilla call and put option pricing formula and martingale method to get the closed form solution of fixed strike and floating strike Asian option with geometric average assets prices in a discrete situation,respectively.
Key words: Asian option; geometric average; option pricing
亚式期权是金融市场上最活跃的奇异期权之一,其主要交易形式为场外交易.由于亚式期权的损益不仅依赖于到期时标的资产的价格,还依赖于标的资产在有效期内某一段时间内的某种平均值,因此,它可以有效地避免投资者通过操纵标的资产价格获利的可能性.同时,由于亚式期权的价值比标准期权的价值更为便宜,因此,它在股票、商品、利率、外汇、能源、以及电力工业等实际市场中有着非常广泛的应用.亚式期权根据采用的平均不同,可分为算术平均亚式期权与几何平均亚式期权;根据支付函数(Payoff)的不同,又可分为固定执行价格看涨期权、固定执行价格看跌期权、浮动执行价格看涨期权以及浮动执行价格看跌期权.为了处理方便,人们通常是在连续监控平均的情况下取得相应的定价公式,例如,文献[1-7]中利用各自不同的方法对连续监控情形下的几何平均亚式期权进行了定价研究,并得出了相应的定价公式.为了更加符合实际,文献[8]利用风险中性定价原理推导出了离散时间几何平均固定执行价格亚式期权的定价公式,文献[9]对离散监控下欧式风格亚式期权(European-style Asian option)的定价方法进行了研究.本文在离散监控条件下,对几何平均进行适当变换后,分别求出了固定执行价格亚式期权和浮动执行价格亚式期权的定价公式.
1几个基本假设与几何平均的相关处理
本研究是基于Black-Scholes模型下进行的.令t时刻标的资产的价格为S(t),它满足
dS(t)=rS(t)dt+σS(t)dW(t),
(1)
其中r为无风险利率,σ为标的资产价格的波动率,{W(t):0≤t≤T}为标准维纳过程.由式(1)不难得到
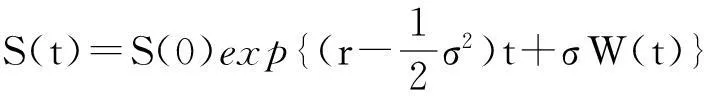
(2)
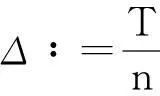
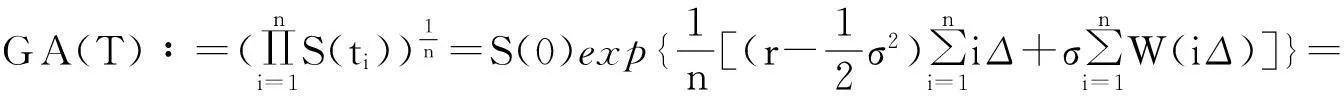
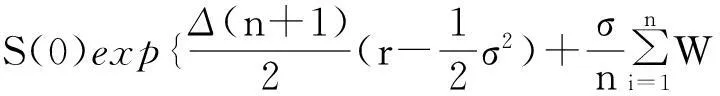
(3)
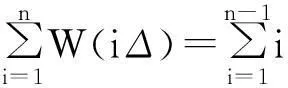
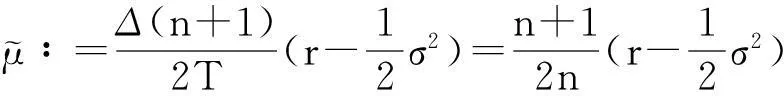
(4)

(5)
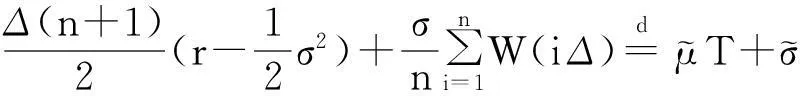


(6)
容易验证式(6)是初值为
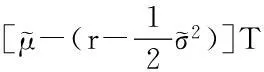
(7)
的微分方程

(8)
的解.也就是说,离散监控下的几何平均满足初值为式(7)的微分方程(8).
2固定执行价格亚式期权的定价
固定执行价格亚式看涨期权与看跌期权的支付函数分别为
max{GA(T)-K,0},max{K-GA(T),0},
(9)
其中K为执行价格.由GA(T)的运动方程(8)与支付函数(9)的形式不难看出,在Black-Scholes模型下,可以把函数(9)看成是以GA(t)为标的资产价格的标准欧式看涨期权的支付函数,因此,可以直接利用Black与Scholes[10]提出的标准欧式看涨期权的定价公式:
固定执行价几何平均看涨期权的定价公式为
FGC(0)=GA(0)e-qTN(d1)-Ke-rTN(d2),
(10)
固定执行价几何平均看跌期权的定价公式为
FGP(0)=Ke-rTN(-d2)-GA(0)e-qTN(-d1),
(11)

3浮动执行价格亚式期权的定价
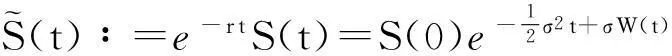
(12)
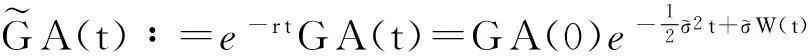
(13)
称V(t)∶=e-r(T-t)E(f(S(T),GA(T))|Ft)为t时刻资产组合的资本过程,其中f(S(T),GA(T))为浮动执行价格亚式期权的支付函数.看涨期权时为fc(S(T),GA(T))=max{S(T)-GA(T),0},看跌期权时为fp(S(T),GA(T))=max{GA(T)-S(T),0}.令
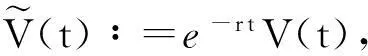
(14)
并称式(14)为折现的资本过程.注意到V(T)=E(e-r(T-t)f(S(T),GA(T))|FT)=f(S(T),GA(T)),这说明可以用V(T)来得到支付函数f(S(T),GA(T))的复制.对式(12)和式(13)使用伊藤公式,不难得出:

(15)
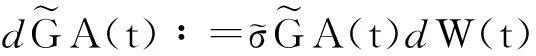
(16)
且当s (17) (18) 再由式(15)可以把式(18)改写成 (19) 由式(12)、(14)和(19),经简单的计算可以得到 (20) 令 (21) 其中{B(t),0≤t≤T}表示无风险资产的价格过程,则式(20)可改写成 dV(t)=β(t)dS(t)+γ(t)dB(t), (22) 而由式(21)可以得到 V(t)=β(t)S(t)+γ(t)B(t). (23) 再由式(22)和(23)可知,资本过程{V(t):0≤t≤T}为自筹资产组合,因此V(0)就是要求得的期权价值: (24) 这里,只对看涨期权的情形给出求解过程即可,看跌期权的情形可类似求得.由于看涨期权时的支付函数为fc(S(T),GA(T))=max{S(T)-GA(T),0},从而 (25) (26) 参考文献: [1]章珂,周文彪,沈蓉芳.几何平均亚式期权的定价方法[J].同济大学学报,2001,29(8):924-927. [2]詹惠蓉,程乾生.亚式期权在依赖时间的参数下的定价[J].管理科学学报,2004,7(5):24-36. [3]肖文宁,王杨,张寄洲.几何平均亚式期权定价方法的探析[J].应用数学,2005,18(2):253-259. [4]杜雪樵,沈明轩.依赖时间参数下几何平均亚式期权的定价[J].合肥工业大学学报(自然科学版),2007,6:206-208. [5]罗庆红,杨向群.几何型亚式期权的定价研究[J].湖南文理学院学报(自然科学版),2007,3:5-7. [6]柳洪恩,孔繁亮.几何型亚式期权定价中的鞅方法[J].哈尔滨理工大学学报,2010,15(1):80-82. [7]王红娜.依赖于时间的跳跃-扩散型几何平均亚式期权的定价[J].江苏师范大学学报,2012,30(2):24-28. [8]金春红,隋振婥.离散几何平均价格亚式期权的定价[J].辽宁大学学报(自然科学版),2006,33(2):166-167. [9]WilliamWYHsu,LyuuYuh-Dauh.EfficientpricingofdiscreteAsianoptions[J].AppliedMathematicsandComputation,2011,217:9875-9894. [10]FischerBlack,MyronScholes.Thepricingofoptionsandcorporateliabilities[J].TheJournalofPoliticalEconomy,1973,81(3):637-654.