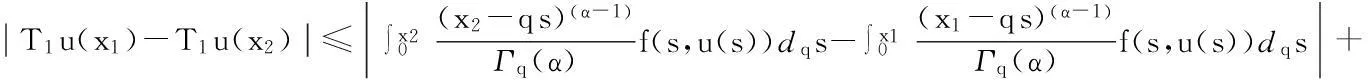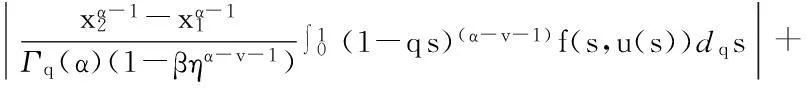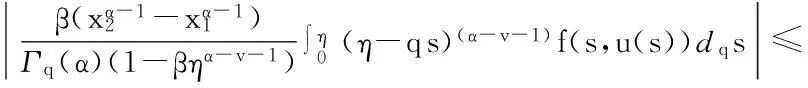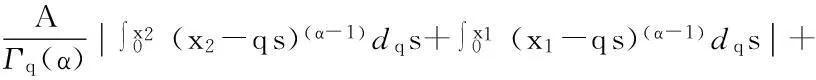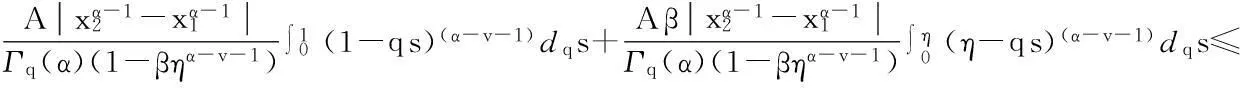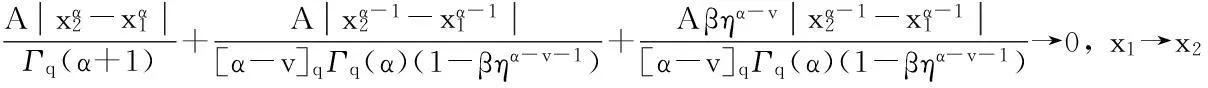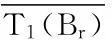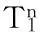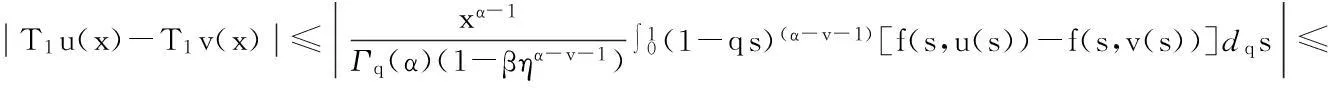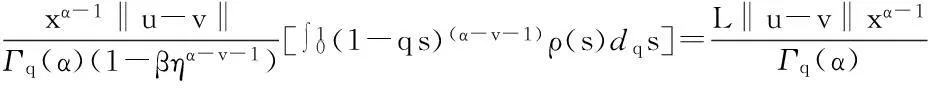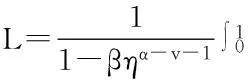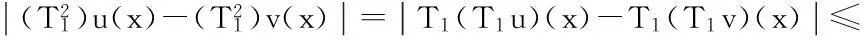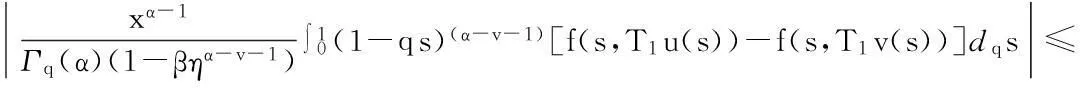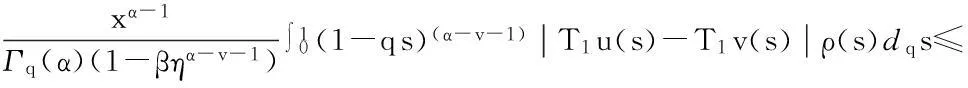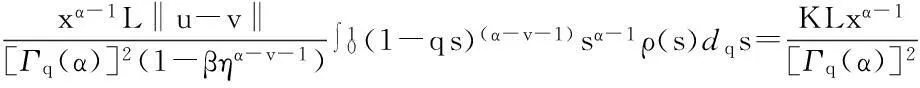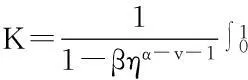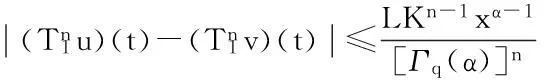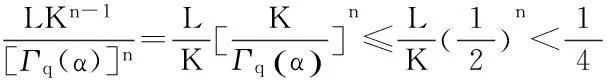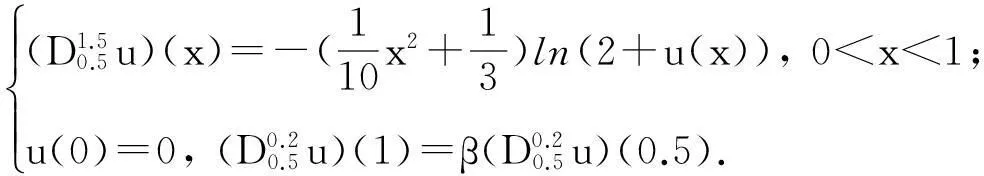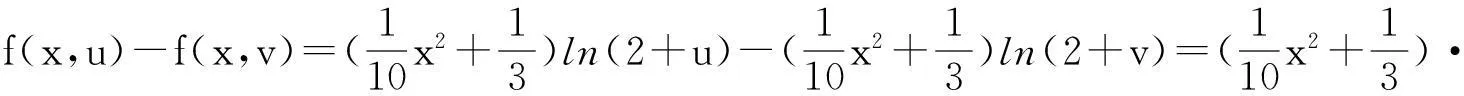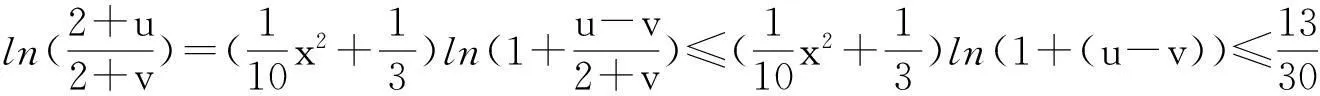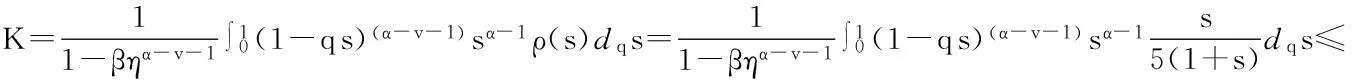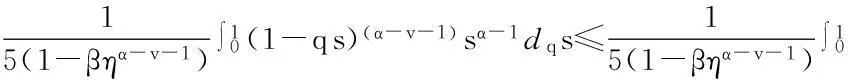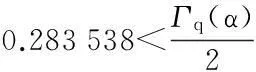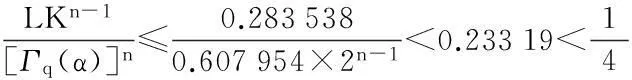一类带有分数阶边值条件的分数阶q-差分方程解的存在性

一类带有分数阶边值条件的分数阶q-差分方程解的存在性

范成涛,葛琦*

( 延边大学理学院 数学系，吉林 延吉 133002 )

摘要：研究了一类带有分数阶q-差分边值条件的分数阶q-差分方程解的存在性和唯一性.首先分析了格林函数的一些性质；其次分别利用完备度量空间上的不动点定理、Banach空间上的Schauder不动点定理和Banach压缩映像原理，证明了该方程解的存在性和唯一性；最后通过实例验证了本文所得结论的正确性.

关键词：分数阶q-差分； 完备度量空间； 不动点定理； 解的存在性和唯一性

收稿日期：2015-01-12*通信作者： 葛琦(1975—)，女，副教授，研究方向为微分方程理论及其应用.

基金项目：国家自然科学基金资助项目(11161049)；吉林省教育厅“十二五”科技项目(012015042)

文章编号：1004-4353(2015)03-0207-08

中图分类号：O175.6

Existence of solutions for a class of fractionalq-differences equation with fractional boundary value conditions

FAN Chengtao,GE Qi*

(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002，China)

Abstract：We study the existence and uniqueness of solutions for a class of the fractional q-differences equation with the fractional q-differences boundary conditions. Firstly,we analyze some properties of the Green function. Secondly,the existence and uniqueness of the solutions of the equation are proved by using the fixed point theorem in complete metric space,Schauder fixed point theorem in Banach space and Banach contraction principle. Finally,the correctness of the conclusion in this paper is verified by some examples.

Key words： fractional q-differences; complete metric space; fixed point theorem; existence and uniqueness of solutions

0引言

近年来，q-差分微积分理论在数学物理问题、动力系统和量子模型等科学领域被广泛应用[1-2].q-微积分概念是由Jackson于1910年提出的[3-4]，之后由Al-Salam[5]和Agarwal[6]给出了分数阶q-微积分的基本概念和性质.近年来，关于分数阶q-差分方程边值问题解存在性的研究受到人们关注，并取得了许多成果[7-13]，但这些研究成果中大多数研究的是带有整数阶边值条件的分数阶q-差分方程的解[9-13].本文研究带有分数阶边值条件的分数阶q-差分方程

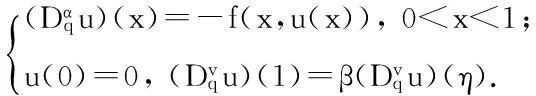
(1)

其中1<α<2,01,0<η<1,0≤β<1,f∶[0,1]×[0,+∞)→[0,+∞)为连续函数.本文将分别利用完备度量空间上的不动点定理、Banach空间上的Schauder不动点定理和Banach压缩映像原理，讨论方程(1)正解的存在性和唯一性.

1预备知识

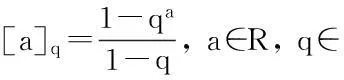
定义2[14]幂指函数(a-b)n的q-类似定义为：

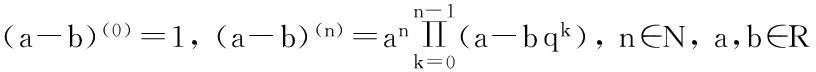
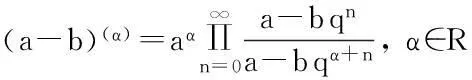
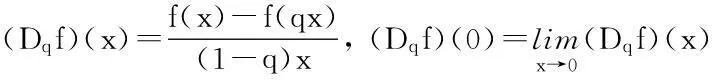
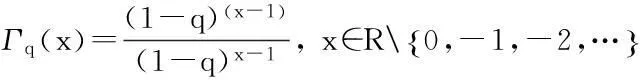
定义5[14]Riemann-Liouville型分数阶q-积分定义为:

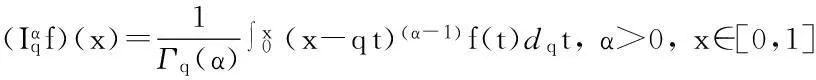
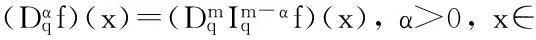
定义6[15]称函数φ为变距离函数，若函数φ∶[0,∞)→[0,∞)满足:(i) 是连续函数，并且是递增的；(ii)φ(t)=0，当且仅当t=0.

性质1[14]若α>0,a≤b≤t，则(t-a)(α)≥(t-b)(α).

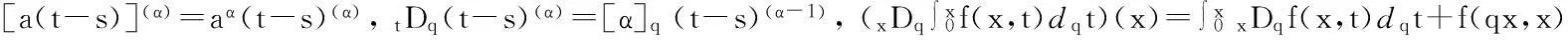
引理1[14]设α>0,p是正整数，则

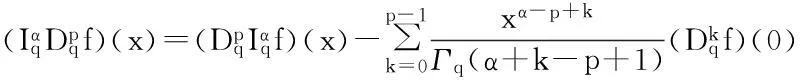
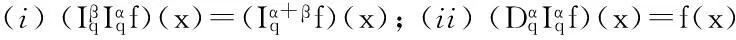
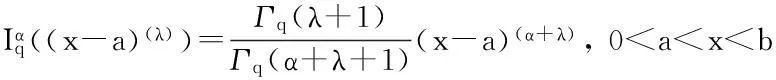
引理4[15]设(X,≤)是一个偏序集，并假设存在X上的一个度量d，使得(X,d)是一个完备度量空间.假设下列条件成立：

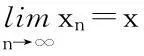
(ii) 对x,y∈X存在z∈X，使得z与x,y是可比较的；

(iii)F∶X→X是递增映射，对于任意x,y∈X，且x≥y，满足

ψ(d(F(x),F(y)))≤ψ(d(x,y))-φ(d(x,y)) ,

(2)

这里ψ,φ是变距离函数；

(iv) 存在x0∈X，使得x0≤F(x0).

那么F在X内存在唯一的不动点.

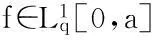
2Green函数及其性质

定理1设1<α<2,01,0<η<1,0≤β<1，若h∈C[0,1]，则分数阶q-差分方程

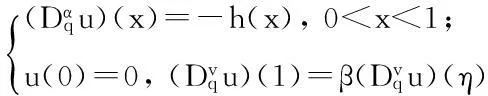
(3)

有唯一解：

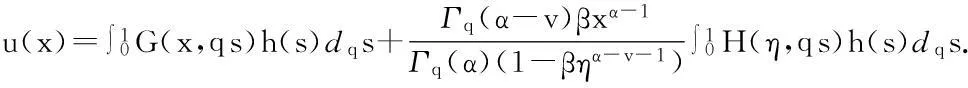
(4)

其中

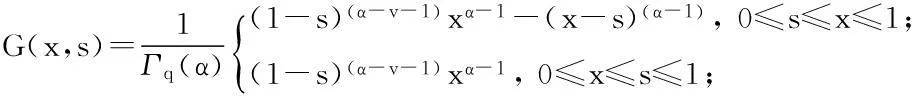
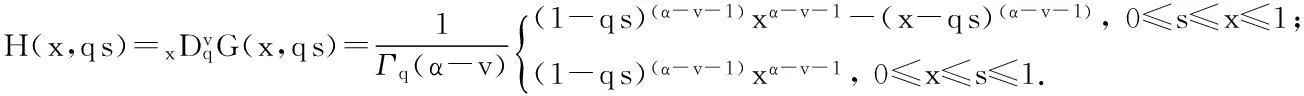
证明假设u(x)是问题(3)的解，则由引理1有

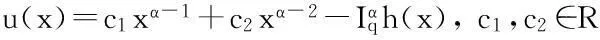
(5)

由边值条件u(0)=0解得c2=0.根据定义5、引理2和引理3有

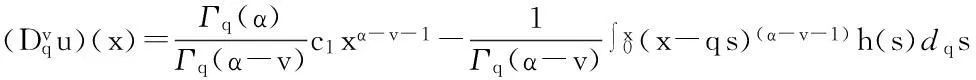
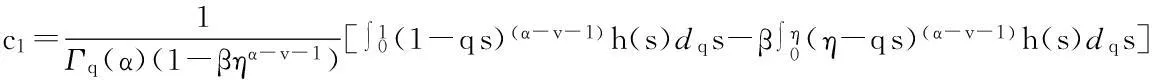
(6)

从而有

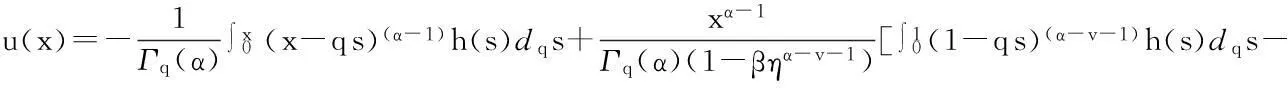
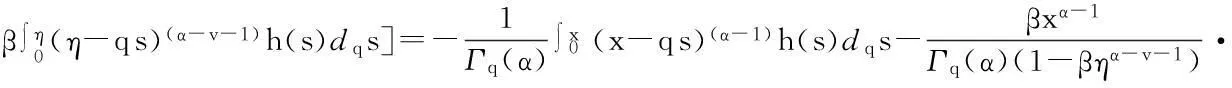
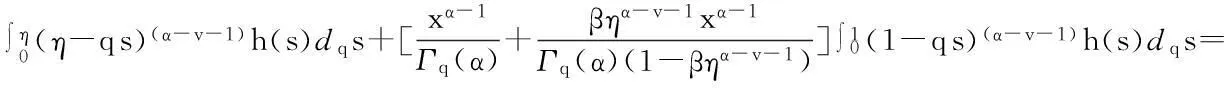
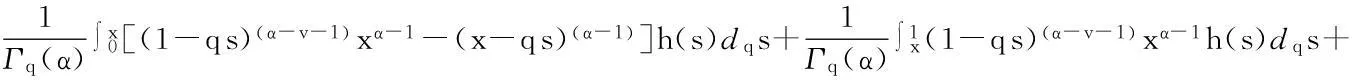
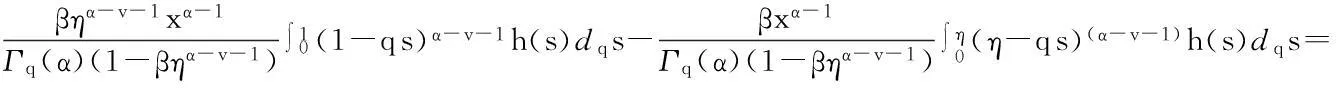
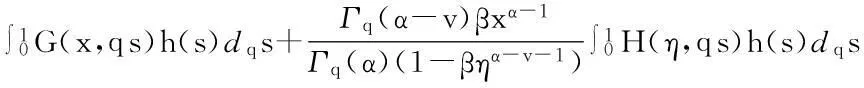
定理2Green函数G(x,s)具有下面的性质：

(i)G(x,s)是连续函数，且G(x,qs)≥0，x,s∈[0,1]；

(ii)G(x,qs)≤G(qs,qs)，x,s∈[0,1].

证明设h1(x,qs)=(1-qs)(α-v-1)xα-1-(x-qs)(α-1),0≤qs≤x≤1;h2(x,qs)=(1-qs)(α-v-1)xα-1,0≤x≤qs≤1.

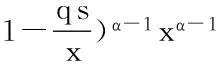
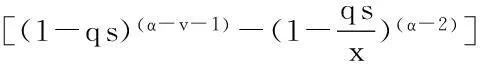
注1根据定理2易知H(x,qs)≥0.

注2如果定理1中h(x)≥0,x∈(0,1]，那么方程(2)的解u(x)≥0.

3主要结果及其证明

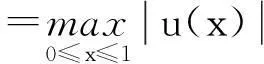
定理3假设如下条件(H1)和(H2)成立，则方程(1)存在唯一正解u(x)：

(H1)函数f∶[0,1]×[0,+∞)→[0,+∞)是连续函数,并且f关于第2个变量是递增的，同时满足f(x,u(x))≠0,x∈(0,1)；

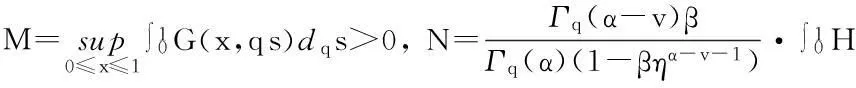
证明在B=C[0,1]上定义锥P={u∈B:u(x)≥0}，由于P是B的闭子集，因此(P,d)是一个完备度量空间.定义算子T∶P→B如下：

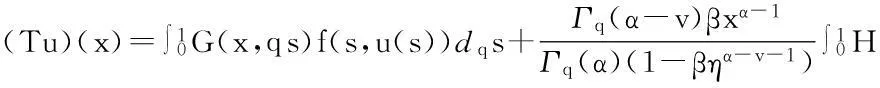
由定理2和条件(H1)可知T(P)⊂P.

首先证明引理4中的所有条件都成立.事实上,对于u,v∈P且u≥v有

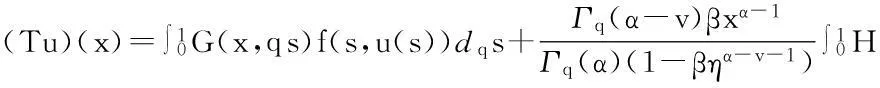
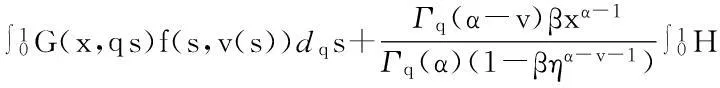
故有算子T是一个递增算子.此外，由条件(H2)，对于u,v∈P且u≥v有

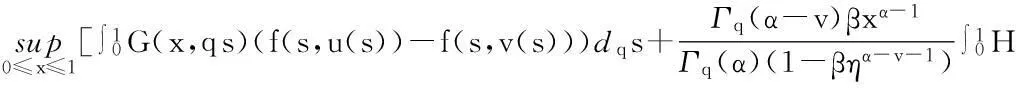
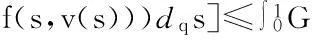
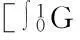
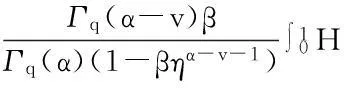
‖u-v‖-[‖u-v‖-ln(‖u-v‖+1)]=d(u,v)-[d(u,v)-ln(d(u,v)+1)].

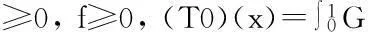
其次证明零函数不是算子T的不动点.事实上,假设零函数是算子T的不动点，则对于x∈[0,1]有

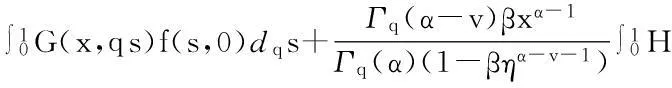
由于G(x,qs)≥0,H(η,qs)>0,f(x,u(x))≥0,则G(x,qs)f(s,0)=0,H(η,qs)f(s,0)=0.因当x≠0,1时,有G(x,qs)>0,故有f(s,0)=0，这与f(x,u(x))≠0,x∈(0,1)矛盾，所以零函数不是T的不动点.

最后，在f(x,u(x))≠0,x∈(0,1)的假设下，证明方程(1)的解u(x)>0,x∈(0,1).事实上，假设存在x0∈(0,1)，使得u(x0)=0，由式(4)有

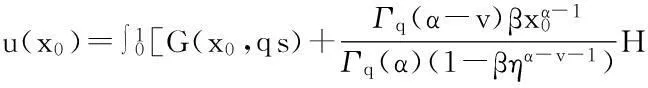
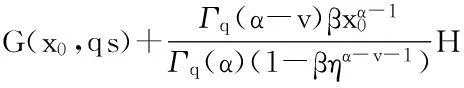
下面利用Banach空间上Schauder不动点定理和Banach压缩映像原理,在f∶[0,1]×[0,+∞)→[0,+∞)连续的假设下，证明方程(1)解的存在性和唯一性.定义算子T1∶B→B如下:

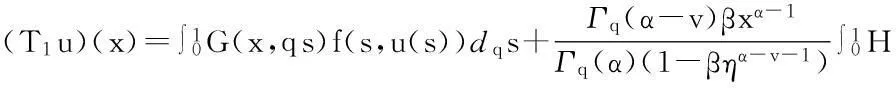
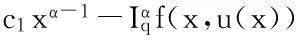
这里c1如式(6)所示，显然T1的不动点是方程(1)的解.

定理4假设f(x,u)满足如下条件(H3)，则方程(1)至少有一个非负解：

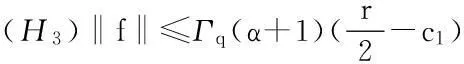
证明定义算子T1∶B→B，有

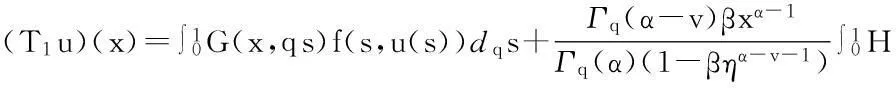
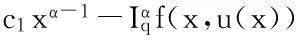
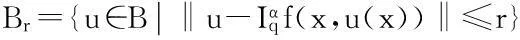
首先证明T1是Br到Br上的映射.事实上，根据条件(H3)和引理5,对于u∈Br有

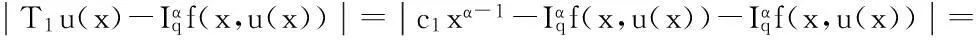
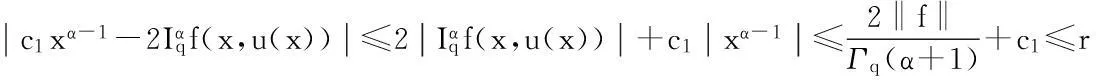
因此，T1是Br到Br上的映射.

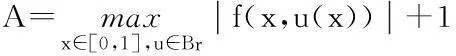
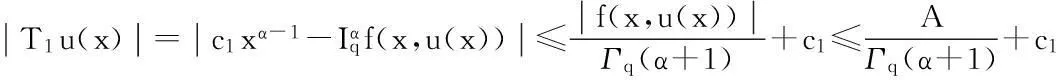
因此，T1(Br)是一致有界的.

最后证明T1(Br)是等度连续的.对于u∈Br,x1,x2∈[0,1]，且x1

定理5假设如下条件(H4)和(H5)成立，则方程(1)存在唯一解u(x)：

4应用举例

例1考虑方程

(7)

例2考虑方程

(8)

参考文献：

[1]PageDN.Informationinblackholeradiation[J].PhysRevLett,1993,71(23):3743-3746.

[2]YoumD. q-Deformedconformalquantummechanics[J].PhysRevD,2000,62(9):095009.

[3]JacksonFH.Onq-definiteintegrals,Quart[J].JPureApplMath,1910,41:193-203.

[4]JacksonFH. q-DifferenceequationsAmer[J].JMath,1910,32(4):305-314.

[5]Al-SalamWA.Somefractionalq-integralsandq-derivatives[J].ProcEdinbMathSoc,1996,15(2):135-140.

[6]AgarwalRP.Certainfractionalq-integralsandq-derivatives[J].ProcCambridgePhilosSoc,1996,66:365-370.

[7]NeamatyA,YadollahzadehM,DarziR.Existenceofsolutionforanonlocalboundaryvalueproblemwithfractionalq-derivatives[J].JournalofFractionalCalculusandApplications,2015,6(2):18-27.

[8]AhmadB,NietoJJ,AlsaediA,etal.Existenceofsolutionsfornonlinearfractionalq-differenceintegralequationswithtwofractionalordersandnonlocalfour-pointboundaryconditions[J].JournaloftheFranklinInstitute,2014,351:2890-2909.

[9]YangWengui.Anti-periodicboundaryvalueproblemsinvolvingnonlinearfractionalq-differenceequations[J].MalayaJournalofMatematik,2013,4(1):107-114.

[10]AhmadB,NtouyasS,PurnarasI.Existenceresultsfornonlocalboundaryvalueproblemsofnonlinearfractionalq-differenceequations[J].AdvDifferEqu,2012,140:1-15.

[11]El-ShahedM,HassanHA.Positivesolutionsofq-differenceequation[J].ProcAmerMathSoc, 2010,138:1733-1738.

[12]LiXinhui,HanZhenlai,SunShurong,etal.Boundaryvalueproblemsforfractionalq-differenceequationswithnonlocalconditions[J].AdvDifferEqu,2014(2014):1-16.

[13]WangJufang,YuChanglong,GaoYanping.Positivesolutionsforaclassofsingularboundaryvalueproblemswithfractionalq-differenceequations[J].JournalofFunctionSpaces,2015,2015:1-8.

[14]孙明哲，韩筱爽.一类分数阶q-差分边值问题的正解[J].延边大学学报版(自然科学版)，2013,39(4):252-255.

[15]HarjaniJ,SadaranganiK.Generalizedcontractionsinpartiallyorderedmetricspacesandapplicationstoordinarydifferentialequations[J].NonlinearAnalysis,2010,72:1188-1197.

[16]AnnabyMH，MansourZS.q-FractionalCalculusandEquations[M].BerlinHeidelberg:Springer-Verlag, 2012.

[17]RicardoAlmeida,NatáliaMartins.Existenceresultsforfractionalq-differenceequationsoforderwiththree-pointboundaryconditions[J].CommunicationsinNonlinearScienceandNumericalSimulation,2014,19(6):1675-1685.