混杂钢纤维超高性能混凝土梁裂缝分形理论研究

范小春，葛 腾，梁天福

(1.武汉理工大学土木工程与建筑学院，武汉 430070；2.武汉地铁集团建设总部，武汉 430000)

0 引 言

随着现代建筑对混凝土强度和耐腐蚀性要求的提高，超高性能混凝土越来越受到重视[1]。但普通钢筋易腐蚀且未能充分发挥超高性能混凝土高强、高韧和高耐久性的特性，玄武岩纤维增强复合材料(basalt fiber reinforced plastic， BFRP)筋是纤维增强聚合物的一种，因其极高的抗拉强度、耐腐蚀和抗疲劳等优势，可以代替传统普通钢筋[2-4]。同时，超高性能混凝土中的钢纤维可以有效改善BFRP筋因弹性模量低而导致的结构裂缝宽、变形大等缺陷，凸显钢纤维的作用[5-7]。另外，有学者[8-12]研究表明通过裂解废旧轮胎钢丝得到的废旧轮胎钢纤维(waste tire steel fiber， WTSF)可以替代工业钢纤维(industrial steel fiber， ISF)，这样不仅可优化超高性能混凝土的经济性，而且满足了当今社会对环境友好的要求，实现可持续发展。

分形几何学(fractal geometry)是20世纪重要的数学发现之一，主要用来研究自然界非规则的图形。混凝土破坏裂缝往往具有不规则、非线性等特征，许多学者用分形理论对此进行研究，从而预测结构的破坏形态特征或分析结构的力学性能。于江等[13]利用分形理论探究了剪跨比和配筋率对无腹筋混凝土梁剪切性能的影响；Akhavan等[14]研究了裂缝的宽度、弯曲度和表面粗糙度的分形特征，并且根据分形的自相似性特征修正了混凝土使用寿命预测模型；焦楚杰等[15]研究了高强混凝土(high strength concrete， HSC)动态损伤后的分形特征，结合试验数据推导出分形损伤演化的HSC动态损伤模型，证实了分形理论在动态冲击试验中的应用价值。上述研究表明可以通过分形理论研究分形维数与混凝土裂缝损伤之间的关系，从而有望为BFRP筋混杂钢纤维超高性能混凝土梁受弯性能分析提供帮助。

本文基于不同WTSF取代率的BFRP筋混杂钢纤维超高性能混凝土梁的受弯试验结果，利用分形理论研究试验梁表面裂缝演化过程和分布特征，得到不同WTSF取代率下各试验梁表面裂缝分布的分形维数，研究WTSF取代率对梁分形维数的影响，并分别拟合WTSF取代率与极限荷载下各梁全梁区和纯弯段分形维数的函数关系，分析施加的荷载大小、跨中挠度、最大裂缝宽度三者与分形维数之间的关系，研究结果可以为BFRP筋混杂钢纤维超高性能混凝土梁的应用提供参考。

1 实 验

1.1 试验材料

制备混杂钢纤维超高性能混凝土所需的原材料包括：P·O 42.5普通硅酸盐水泥、硅灰、S95级矿粉、石英砂、聚羧酸高效减水剂、ISF(高强镀铜微细钢纤维)、WTSF(废旧轮胎钢纤维)。混凝土的配合比见表1。BFRP筋用作下部受力钢筋，采用直径为12 mm的深螺纹BFRP筋，长度为1 980 mm，架立筋和箍筋均采用直径为8 mm的HPB300型光圆钢筋。筋材的各项性能参数见表2。ISF和WTSF相关性能参数见表3。

表1 混杂钢纤维超高性能混凝土配合比Table 1 Mix proportion of hybrid steel fiber ultra-high performance concrete

表2 筋材性能参数Table 2 Performance parameters of reinforcement

表3 ISF和WTSF相关参数Table 3 Relevant parameters of ISF and WTSF

续表

1.2 试验梁设计

制作6根不同WTSF取代率的BFRP筋混杂钢纤维超高性能混凝土梁，配筋率均为1.12%，钢纤维的总体积掺量均为2.5%，WTSF对ISF的取代率分别为0%、20%、40%、60%、80%和100%。6根试验梁的尺寸均为120 mm×200 mm×2 000 mm，按照规范要求保护层厚度为15 mm。箍筋间距为100 mm，左右两端各设立8个箍筋，纯弯段不设立箍筋。梁基本参数见表4，配筋示意图如图1所示。

表4 BFRP筋混杂钢纤维超高性能混凝土梁基本参数Table 4 Basic parameters of hybrid steel fiber ultra-high performance concrete beams with BFRP bars

Note: B12 indicates that BFRP bar has a diameter of 12 mm; IU indicates only ISF; WU indicates only WTSF; HU* indicates hybrid steel fiber, the substitution rate of WTSF is *;fcuindicates cube compressive strength;ftsindicates splitting tensile strength.

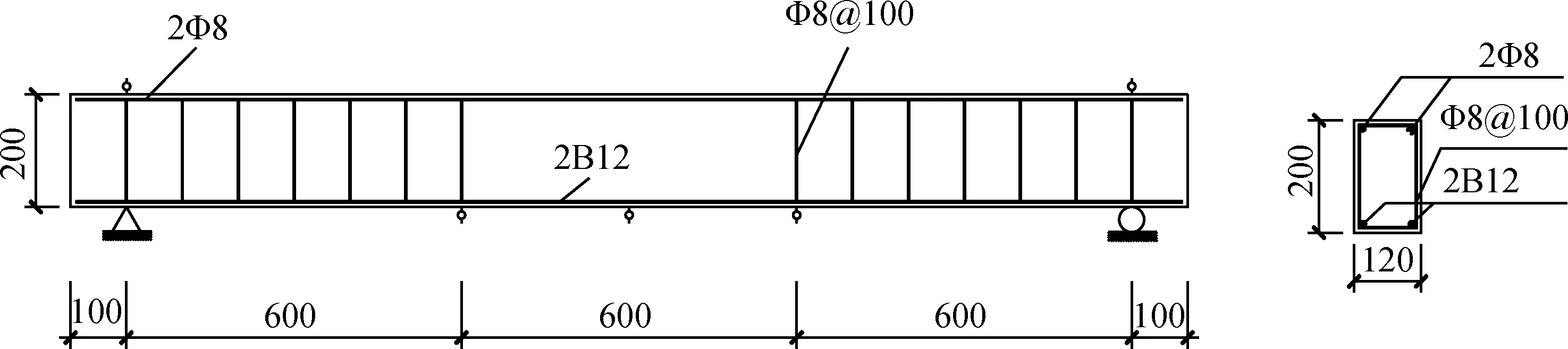
图1 梁配筋示意图(单位：mm)Fig.1 Reinforcement schematic diagram of beams (unit: mm)

1.3 试验加载方案

为了满足试验要求，选用2 000 kN压力机，试验装置及测点布置如图2所示，采用传统四点加载模式，加载速率控制为0.2 kN/s，荷载步距为每级10 kN，临近开裂荷载预估值时，将荷载步距改为每级2 kN，当梁开裂后再恢复至每级10 kN，每级持荷时长为5 min，试验梁现场加载如图3所示。

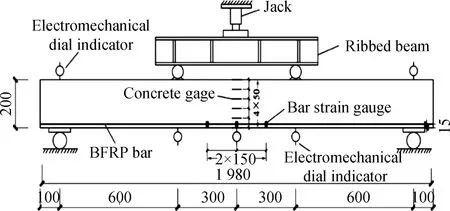
图2 试验装置及测点布置(单位：mm)Fig.2 Loading device and measuring points arrangement (unit: mm)

图3 现场加载试验图(B12HU60)Fig.3 Loading experiment on site (B12HU60)

2 裂缝特征的分形描述

2.1 梁表面裂缝开展过程及分布形态

对6根BFRP筋混杂钢纤维超高性能混凝土梁受弯过程中表面裂缝的演化图按照荷载等级分级绘制，其中极限荷载完全破坏下的裂缝最终分布形态如图4所示。图中(*)表示裂缝编号，按裂缝先后顺序进行标注。

图4 各试验梁在完全破坏下裂缝最终分布形态描绘图Fig.4 Depiction of final crack distribution of each test beam under complete failure

由图4裂缝开展的宏观特征可以看出,不同WTSF取代率的梁的裂缝开展情况区别不大，但是总体趋势是WTSF取代率越高，裂缝数量越多且单条裂缝的分支也越多，这表明WTSF的掺入使混杂钢纤维超高性能混凝土梁的受力变得更不均匀，直接表观特征就是梁表面的裂缝分布也变得更杂乱无章。

2.2 裂缝分形维数的计算

分形几何学中，笼统地把取非整数(分数)的维数称为分形维数。若不规则图形具有分形特征，则表明该图形在某个标度不变区域内满足自相似性，一旦超过这个区域，自相似性就会消失[16]。分形维数的测定有很多种方法：盒计数法、粗糙曲线的圆规曲线法、周长-面积法、表面积-体积法、Sandbox法、面积-回转半径法、变化(variation)法等[17]。本文采用盒计数法测得试验梁表面裂缝的分形维数Df，具体方法如下：构造不同边长r(单位：mm)的正方形网格(称为盒子)覆盖梁表面，分别统计出内含裂缝的格子总数N(r)，而分形维数Df就是当r趋于0时，N(r)增加的对数速率，即lnN(r)-ln(1/r)关系曲线的斜率,见式(1)。如果分形维数Df存在，lnN(r)和lnr符合线性关系，则表明梁表面的裂缝分布可以用分形理论分析，满足分形集的全部特征，在某个标度范围内符合自相似性。

(1)

采用4种不同网格尺寸，r分别为5 mm、10 mm、20 mm、25 mm。网格覆盖的过程以B12HU40为例，如图5所示。

图5 试验梁网格覆盖过程图(B12HU40)Fig.5 Grid coverage process of test beam (B12HU40)

2.3 受弯过程中梁表面裂缝的分形特征

分别对6根BFRP筋混杂钢纤维超高性能混凝土梁在不同荷载作用下的表面裂缝进行分形维数计算,并拟合得出在不同荷载级别下lnN(r)-lnr关系曲线，以验证各试验梁在各种施加荷载值下表面裂缝的分形特性,如图6所示。

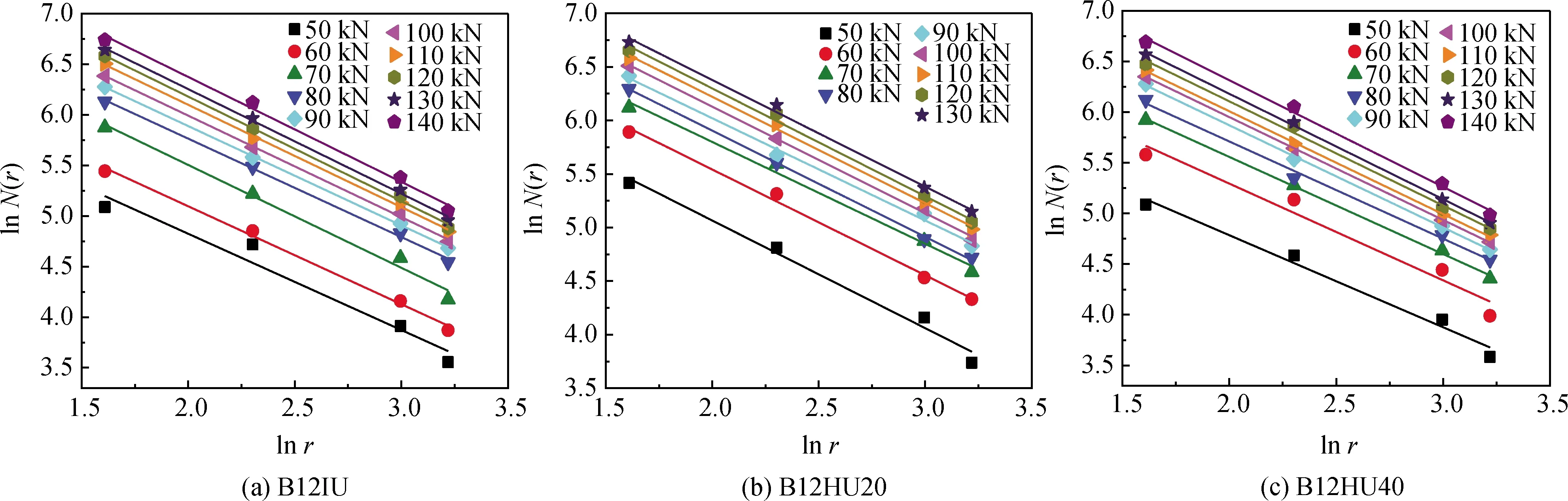
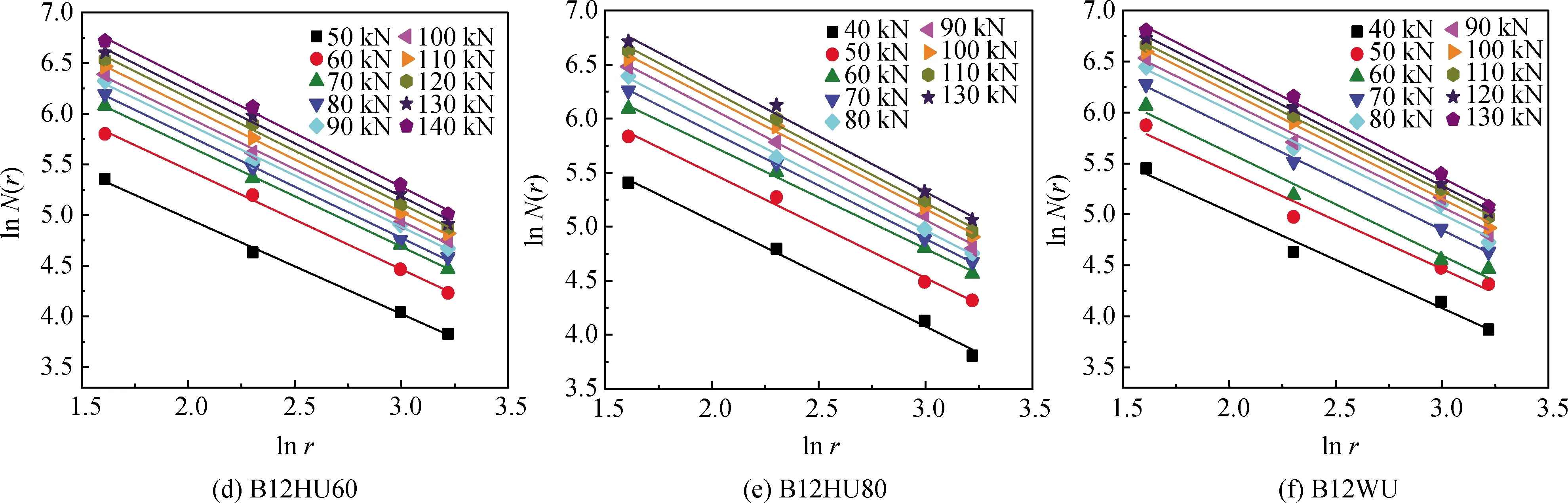
图6 分级荷载下各试验梁的ln N(r)-ln r关系Fig.6 ln N(r)-ln r relation of each test beam under graded load

由图6可以看出，6根梁在开裂初期，表面裂缝均处于发育不成熟阶段，关系曲线的斜率的绝对值小于相应的拓扑维数，即1，因而不具有统计意义下的自相似性。随着荷载持续增大，裂缝开展迅速，曲线斜率的绝对值均大于1，拟合程度很好，不同荷载值下试验梁表面裂缝的lnN(r)-lnr函数曲线呈线性关系，表明梁在受弯开裂至破坏的全过程中表面裂缝的演变满足自相似性。图中曲线斜率的相反数就是该荷载作用下的裂缝的分形维数Df，试验梁各级荷载值下的表面裂缝的分形维数Df及其相关系数R2见表5。

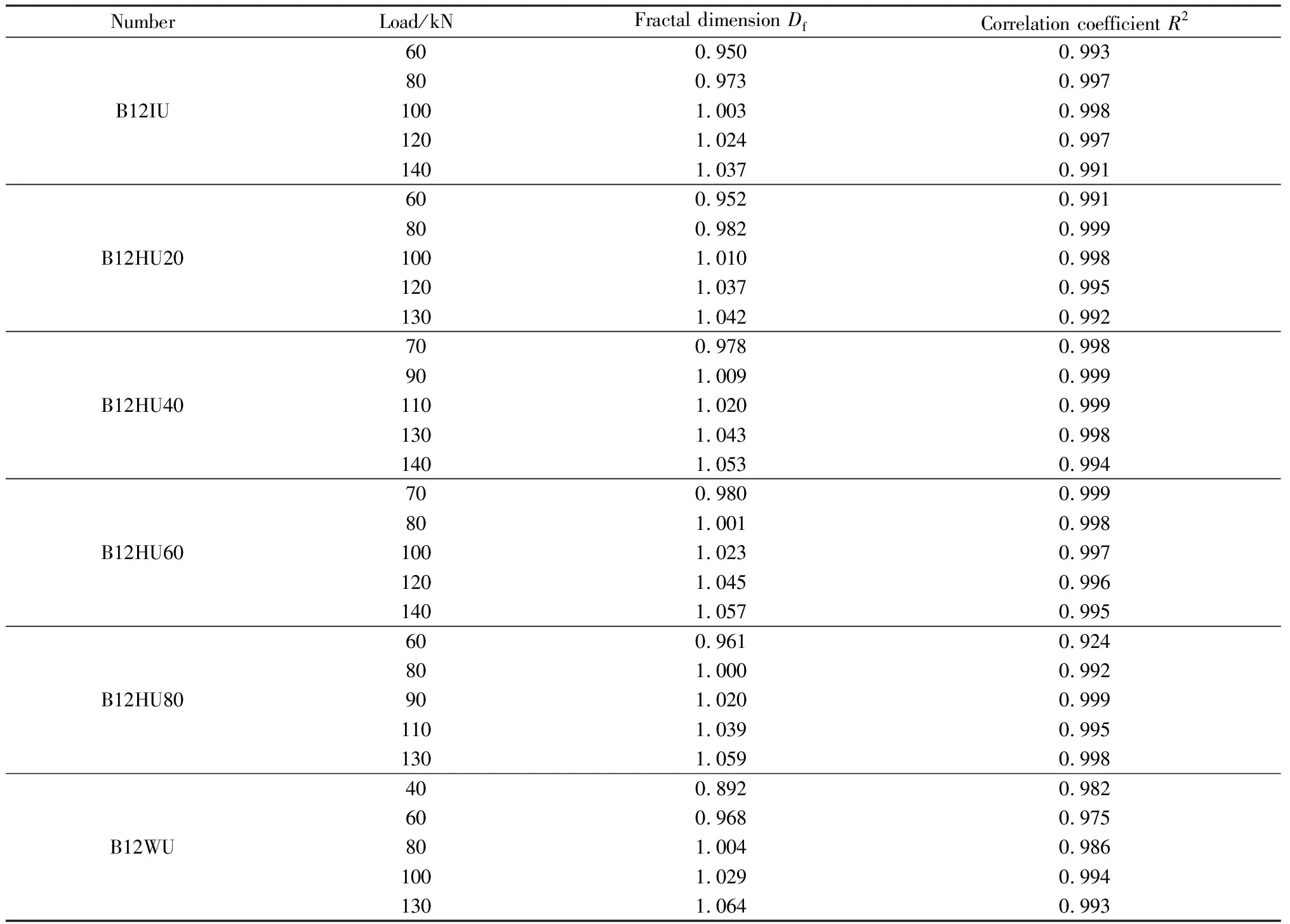
表5 分级荷载下各试验梁表面裂缝的分形维数及其相关系数Table 5 Fractal dimension and correlation coefficient of surface cracks of each test beam under graded load

从表5可以看出，当荷载值增加时，相应梁的表面裂缝的分形维数也增大，梁表面裂缝分形维数越大，表示该梁的开裂越严重，破坏程度越大。同一配筋率下，WTSF取代率越大，分形维数大于拓扑维数1对应的荷载越小，说明WTSF取代ISF会对超高性能混凝土梁开裂产生不利的影响。现有研究[18]表明，试验梁在各级荷载作用下，表面裂缝的分形维数可分为线状、面状和网状三类，1.01～1.40区间属于线状，1.30～1.60区间属于面状，1.50～1.90区间属于网状，由图6和表5分析可知，各试验梁表面裂缝均表现为线状，各组试验梁裂缝的分形维数的变化区间为[0.892,1.064]。

2.4 完全破坏状态下全梁区表面裂缝的分形特征

极限荷载下梁被完全破坏，表面裂缝不再发展，拟合完全破坏状态下各梁表面裂缝的lnN(r)-lnr函数曲线，如图7所示，完全破坏状态下不同WTSF取代率的BFRP筋混杂钢纤维超高性能混凝土梁全梁区表面裂缝分形维数如图8所示，同时拟合了不同WTSF取代率与完全破坏时全梁区表面分形维数的函数关系。

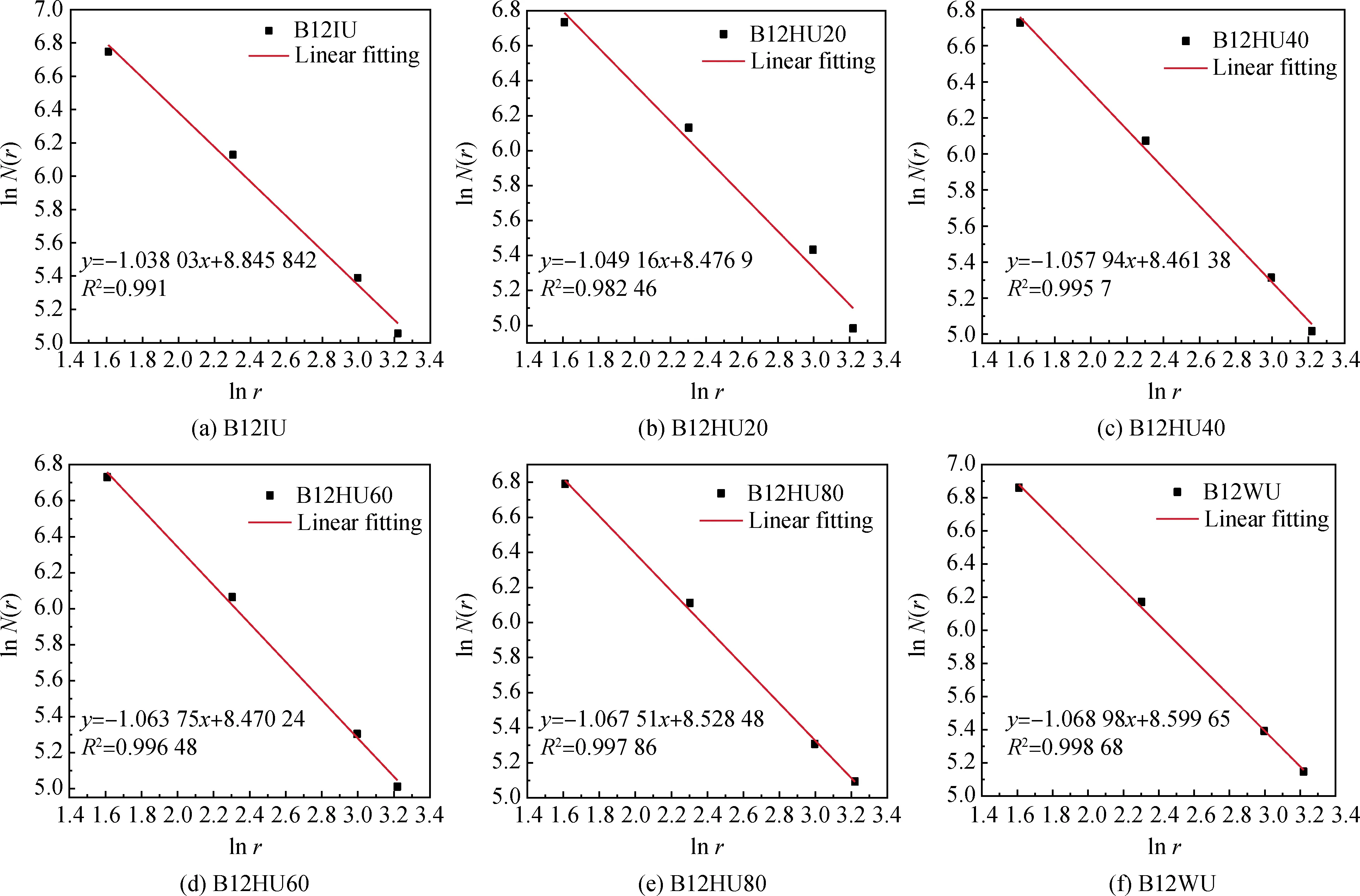
图7 极限荷载下各试验梁全梁区ln N(r)-ln r关系曲线Fig.7 ln N(r)-ln r relation curves of whole beam area of each test beam under ultimate load

图8 极限荷载下各试验梁全梁区的分形维数对比Fig.8 Comparison of fractal dimension of whole beam area of each test beam under ultimate load

由图7可知，在极限荷载下完全破坏时，6根BFRP筋混杂钢纤维超高性能混凝土梁具有很好的分形特征，各试验梁表面裂缝的lnN(r)-lnr曲线拟合程度良好，拟合度均在98%以上。

相同配筋率下，WTSF取代率与各梁破坏时全梁区的分形维数Df1拟合的关系式见式(2)，拟合图见图8。

Df1=1.077 04+{-0.038 99/[1+(x/38.159 89)1.446 27]}

(2)

式中:Df1为梁全梁区表面裂缝分形维数；x为WTSF取代率，%。

由图8和式(2)分析可知,极限状态下相同BFRP筋配筋率的混杂钢纤维超高性能混凝土梁，随着WTSF取代率的增大，全梁区表面裂缝的分形维数增大，都大于1。取代率为0%时分形维数最小，为1.038 03，取代率为100%时分形维数最大，为1.068 98，且取代率小于60%时，裂缝分形维数随着取代率的增大而增长得较快，取代率大于60%时，裂缝分形维数随取代率的增大而增长得较慢。这表明ISF比WTSF更有利于限制梁表面裂缝的开展，宏观表现上也是WTSF取代率越高的梁，其表面裂缝更密集且更不规则，但极限荷载并没有展现出一样的趋势，说明WTSF取代率的提高虽然会在一定程度上对超高性能混凝土开裂产生不利的影响，但却不会降低超高性能混凝土梁的承载力，这可能是由于WTSF形状不规则使其在受力过程中产生多个锚固点，提高了纤维与超高性能混凝土的握裹能力和黏结性能。工程上可选择WTSF取代率为60%的混杂钢纤维超高性能混凝土，既经济又能保证较高的承载能力，若继续增大WTSF取代率，极限荷载会降低，这是因为WTSF长短不一，受力稳定性不高，掺量过高会结团，所以WTSF取代率过高的试验梁极限承载力有所下降。

利用式(2)可以得到配筋率1.12%下任意WTSF取代率的BFRP筋混杂钢纤维超高性能混凝土梁完全破坏时的分形维数，从而可以预测梁裂缝的开展情况，为评价此类构件安全性提供了新的思路。

2.5 完全破坏状态下梁纯弯段表面裂缝的分形特征

由图4可以看出,当各梁处于极限荷载时，其表面裂缝的主要发展位置和形态都略有区别，较直观的特征之一就是纯弯段的裂缝数量和分布不一致。拟合极限荷载作用下完全破坏时各梁纯弯段表面裂缝的lnN(r)-lnr关系曲线，如图9所示，完全破坏状态下不同WTSF取代率的BFRP筋混杂钢纤维超高性能混凝土梁纯弯段裂缝分形维数如图10所示，同时拟合了不同WTSF取代率与完全破坏时梁纯弯段表面分形维数的函数关系。

图9 极限荷载下各试验梁纯弯段ln N(r)-ln r关系曲线Fig.9 ln N(r)-ln r relation curves of pure bending section of each test beam under ultimate load

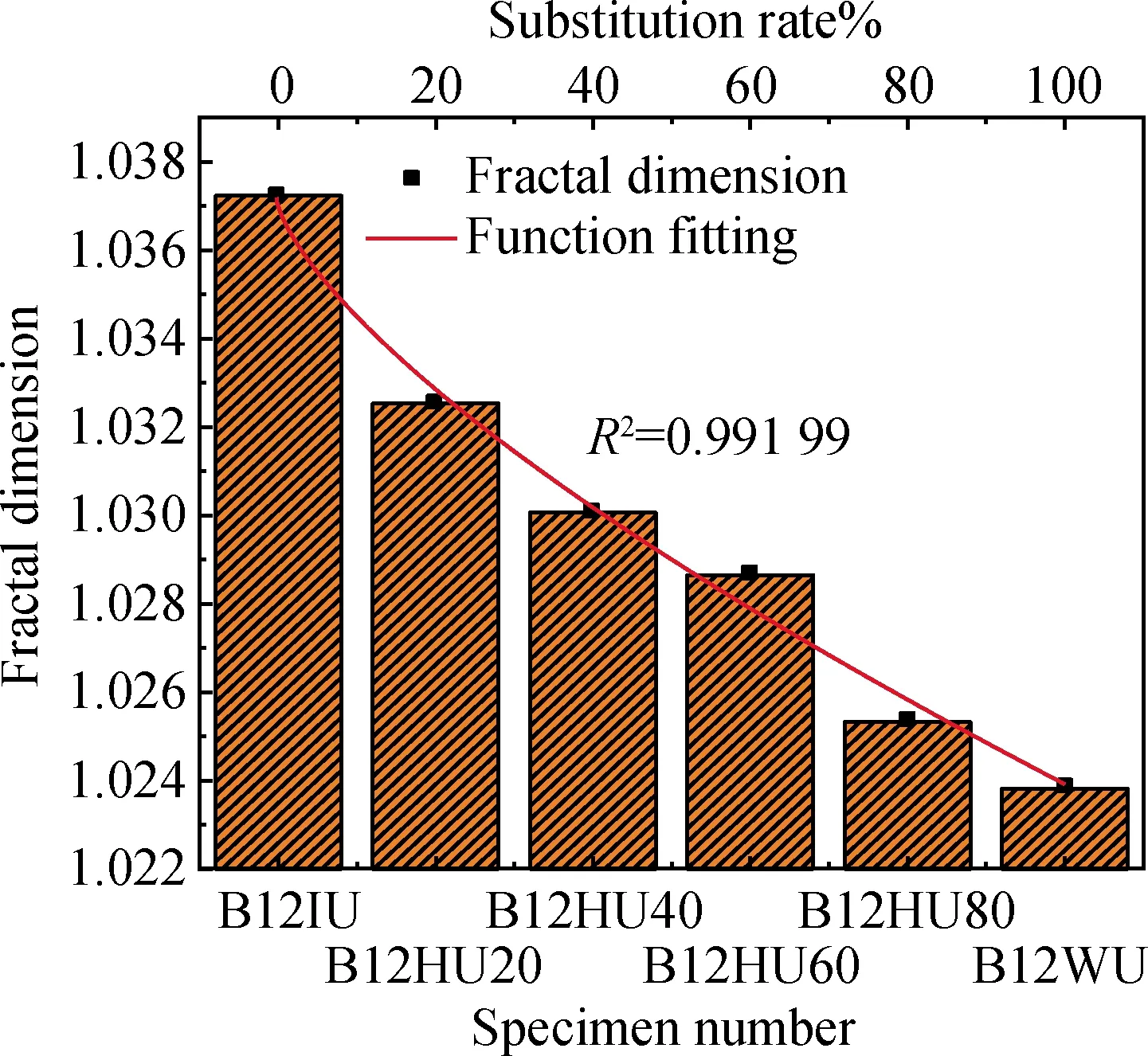
图10 极限荷载下各试验梁纯弯段的分形维数对比Fig.10 Comparison of fractal dimension of pure bending section of each test beam under ultimate load

由图9可知，在极限荷载完全破坏时，6根BFRP筋混杂钢纤维超高性能混凝土梁纯弯段裂缝也同样具有分形特征，拟合度均在98.5%以上。

相同配筋率下，WTSF取代率与各梁破坏时纯弯段的分形维数Df2拟合的关系式见式(3)，拟合图见图10。

Df2=-10.856 5+ {11.893 66/[1+(x/1 640 830)0.7]}

(3)

式中：Df2为梁纯弯段表面裂缝分形维数；x为WTSF取代率，%。

由图10和式(3)分析可知,极限状态下相同BFRP筋配筋率的混杂钢纤维超高性能混凝土梁纯弯段的裂缝分形维数随WTSF取代率的增大而减小，与全梁区的规律正好相反，且均小于极限状态下各全梁区裂缝分形维数，取代率为0%时分形维数最大，为1.037 23，取代率为100%时分形维数最小，为1.023 81。这表明各梁纯弯段裂缝开展的速度低于全梁的平均水平，宏观表现上也是纯弯段的裂缝开展得较慢，同时WTSF的取代会间接影响梁的受力性能，随着WTSF取代率的增大裂缝分布呈现剪弯段数量增多，纯弯段数量减少的趋势。

利用式(3)可以得到配筋率1.12%下任意WTSF取代率的混杂钢纤维超高性能混凝土梁完全破坏时纯弯段的分形维数，为此材料在实际工程上的应用提供理论计算指导。

3 裂缝分形特征与受弯性能之间的关系

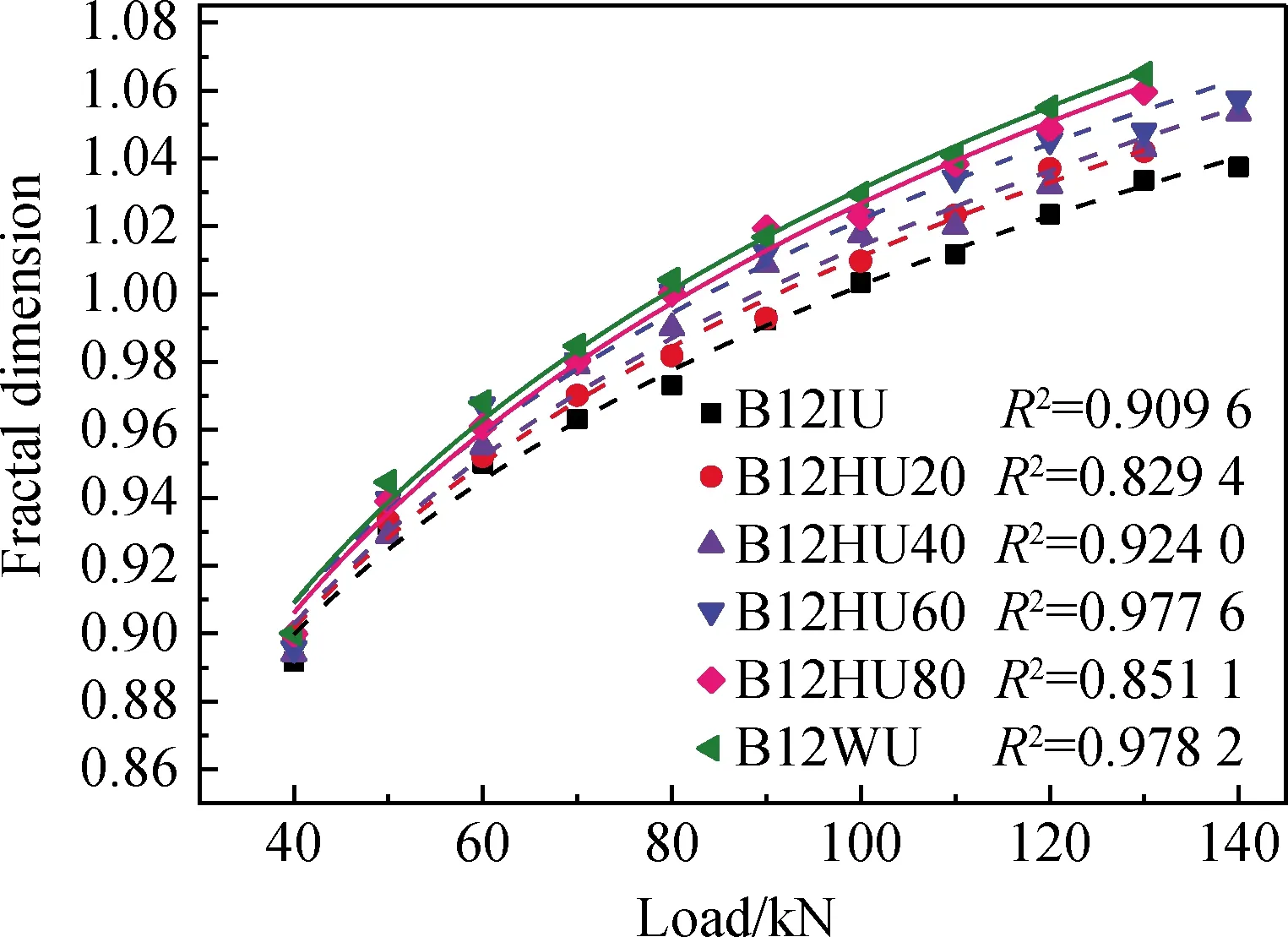
图11 各试验梁分形维数与荷载的关系Fig.11 Relationship between fractal dimension and load of each test beam

3.1 裂缝分形维数与荷载的关系

由上述分析可知，加载过程中和最终破坏时BFRP筋混杂钢纤维超高性能混凝土梁表面裂缝均具有分形特征，由表5中各级荷载值与对应的分形维数值拟合BFRP筋混杂钢纤维超高性能混凝土梁表面裂缝分形维数与施加荷载值的函数曲线，如图11所示。

由图11可以看出,BFRP筋混杂钢纤维超高性能混凝土梁表面的裂缝分形维数与施加荷载值之间均呈典型的对数函数关系，其表达式见式(4)。

Df=AlnP+B

(4)

式中：Df为梁表面裂缝分形维数；P为施加荷载值，kN；A、B为函数系数，其值如表6所示。

表6 各试验梁分形维数与施加荷载值曲线的A和B值Table 6 A and B values of fractal dimension and load curves of each test beam

由图11及表6可以看出,相同配筋率下，不同WTSF取代率时梁开裂初期的分形维数大致相同，随着荷载不断增大，WTSF取代率越大的梁的曲线变化率也越大，说明WTSF取代率的变化对初始裂缝的开展影响不大，但是会影响裂缝开展的速度。上述现象表明，用WTSF取代ISF对BFRP筋混杂钢纤维超高性能混凝土梁的开裂后性能产生少许不利的影响，这是由于WTSF长短不一，稳定性较差，对裂缝的桥接作用不如ISF。

3.2 裂缝分形维数与跨中挠度的关系

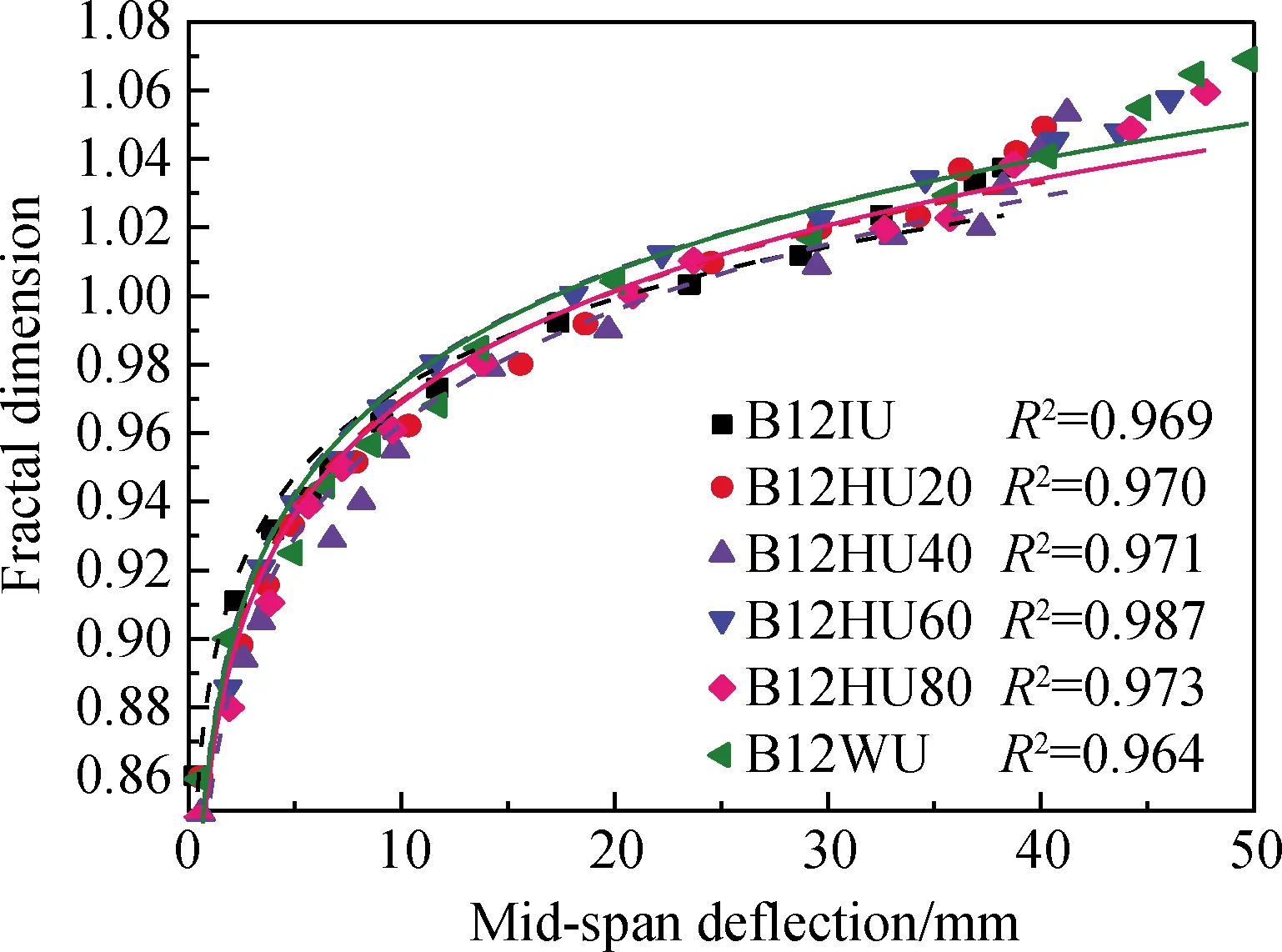
图12 各试验梁分形维数与跨中挠度的关系Fig.12 Relationship between fractal dimension and mid-span deflection of each test beam

统计各试验梁在分级荷载值所对应的跨中挠度和分形维数，拟合BFRP筋混杂钢纤维超高性能混凝土梁表面裂缝分形维数Df与跨中挠度Δ的关系曲线，如图12所示。

由图12可以看出，跨中挠度不断增大，BFRP筋混杂钢纤维超高性能混凝土梁对应的分形维数也增大，两者同样呈对数函数关系，其函数关系见式(5)。

Df=ClnΔ+D

(5)

式中：Df为梁表面裂缝分形维数；Δ为跨中挠度，mm；C、D为函数系数，其值如表7所示。

由图12及表7可以看出，当配筋率相同时，随着WTSF取代率增大，试验梁裂缝分形维数与跨中挠度函数曲线上升得越快，挠度变形相同时，试验梁表面裂缝分形维数也变大，且破坏时的最大跨中挠度和最大分形维数也随之增大，这是因为WTSF限制裂缝开展的能力不如ISF。各试验梁分形维数和跨中挠度的拟合图还有一个共同点就是拟合曲线的末端拟合程度均不高，这是由于各试验梁在临近极限荷载时，裂缝发展迅速，而BFRP筋较高的抗拉强度限制了跨中挠度的增长。

表7 各试验梁分形维数和跨中挠度曲线的C和D值Table 7 C and D values of fractal dimension and mid-span deflection curves of each test beam

3.3 裂缝分形维数与最大裂缝宽度的关系

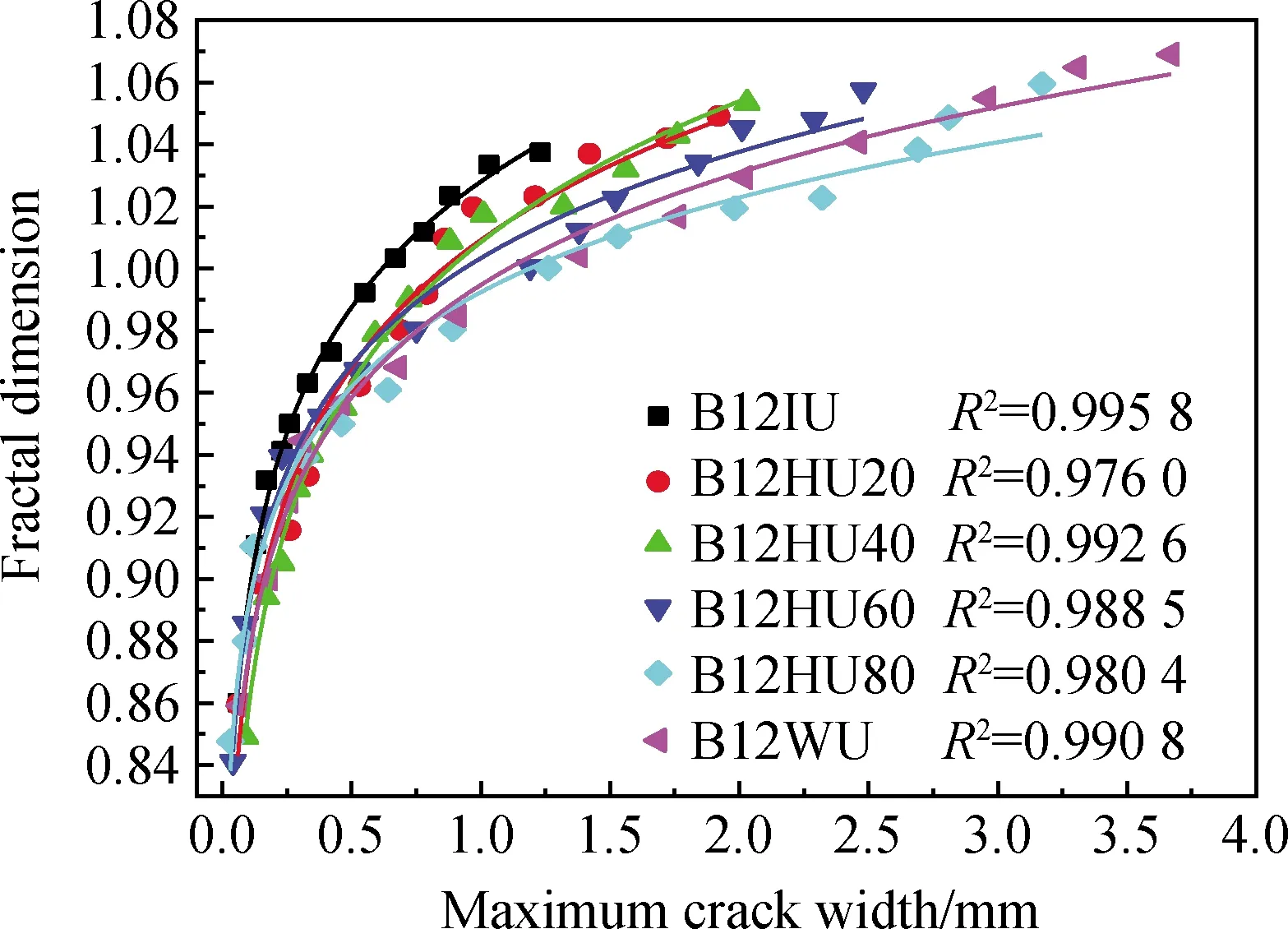
图13 各试验梁分形维数与 最大裂缝宽度的关系Fig.13 Relationship between fractal dimension and maximum crack width of each test beam

统计各试验梁在各级荷载下对应的最大裂缝宽度值和分形维数，拟合BFRP筋混杂钢纤维超高性能混凝土梁表面裂缝分形维数Df与最大裂缝宽度值ωmax的关系曲线，如图13所示。

由图13可以看出，最大裂缝宽度不断增大，BFRP筋混杂钢纤维超高性能混凝土梁对应的分形维数也增大，两者的增长也呈对数函数关系，其函数关系见式(6)。

Df=Elnωmax+F

(6)

式中：Df为梁表面裂缝分形维数；ωmax为最大裂缝宽度，mm；E、F为函数系数,其值如表8所示。

由图13和表8可以看出，试验梁表面裂缝分形维数和最大裂缝宽度曲线变化规律差异较大，相同配筋率下，WTSF取代率越高的梁最大裂缝宽度也越大，同一分形维数下，B12IU试验梁的最大裂缝宽度最小，B12HU80试验梁的最大裂缝宽度最大，表明WTSF可以和ISF一样起到限制裂缝宽度的作用。

表8 各试验梁分形维数和最大裂缝宽度曲线的E和F值Table 8 E and F values of fractal dimension and maximum crack width curves of each test beam

4 结 论

(1)BFRP筋混杂钢纤维超高性能混凝土在受弯过程和完全破坏时表面裂缝的演化均可用分形理论进行研究分析，具有自相似性，分形维数值在[0.892,1.064]区间变化。

(2)极限状态下，WTSF取代率越大，全梁区表面裂缝的分形维数越大，表明WTSF抑制裂缝开展的作用不如ISF，工程上可选用WTSF取代率为60%的梁，既经济又能保证良好的受弯性能；WTSF取代率与各梁破坏时全梁区分形维数的拟合公式为Df1=1.077 04+{-0.038 99/[1+(x/38.159 89)1.446 27]}。

(3)随着WTSF取代率的增加，试验梁在受弯过程中的受力变得更加不均匀，极限状态下试验梁表面纯弯段的裂缝分布变少，分形维数变小；WTSF取代率与各梁破坏时纯弯段分形维数的拟合公式为Df2=-10.856 5+{11.893 66/[1+(x/1 640 830)0.7]}。

(4)施加荷载值、跨中挠度以及最大裂缝宽度与BFRP筋混杂钢纤维超高性能混凝土梁表面裂缝分形维数都呈对数函数关系。WTSF取代率越大，裂缝分形维数与荷载等级、跨中挠度的拟合曲线变化率越大，裂缝开展的速度越快，最大裂缝宽度越大。