练习课：让“问题链”联成“情境串”

陈建中 陈莉莉

摘 要：数学练习课是以学生练习为主要内容的课型，它是新授课的补充和延续，是课堂教学的重要组成部分。但与新授课相比，教师对练习课的设计不够重视和用心。通过访谈身边不同资历的教师，笔者发现练习课普遍以教材中的习题讲练为主，形式单一，学生兴趣不高，教学效果不理想。那么，如何改变练习课“一练到底”的固有模式呢？笔者借着“圆的面积练习”一课把关注点聚焦到“情境串”设计上，试图通过用同一个情境串起练习课的各个环节，通过“问题链”把练习题有效串联，让练习课从“浅层练习”走向“深度学习”，呈现数学练习课的新样态。

关键词：小学数学;圆的面积;问题链;教学情境

人教版数学教材六年级上册第5单元练习十五安排在“圆的面积计算”一课后，主要包括基础题（已知半径或直径求圆或圆环面积的图形题）和拓展题（组合图形面积和周长以及生活实际问题）两部分。

通过对教材内容的梳理及学生易错点的剖析，可以将这些点状、分散的习题加以优化整合，从圆形花坛这一主情境出发，设置一系列内部相关联的情境串起练习的各个环节，使得各练习题之间有效串联，以此增加所学知识的趣味性和吸引力，使学生在掌握知识技能的同时提升数学素养。

一、主情境引入——关注“问题链”，完成基本练习

师：同学们，这节课我们一起对圆的面积进行相关练习。

课件呈现圆形的花坛，同时给出相关信息：公园花坛中心一个自动旋转喷灌装置的射程是8米，它能喷灌的面积是多少？

师：这是求什么？要求面积，我们需要知道什么？这题告诉了我们什么？试着算一算。（學生解答后回顾圆的面积和周长计算公式）

师：如果这道题改成绕小路沿着花坛边走一圈是50.24米，你还能求中间这个圆形花坛的面积吗？你又是怎么思考？（学生解答后反馈回顾求半径和直径的方法）

师：现在，如果要求小路的面积，需要知道哪些条件？

师：如果告诉我们路宽2米，可以怎么计算小路的面积，动手算一算。（学生解答后反馈回顾求圆环面积的方法）

课件呈现的圆形花坛是本节课的主情境，本环节主情境不变，信息不断变化且层层递进，给学生带来感官冲击。通过计算花坛的面积，帮助学生巩固基础题（圆的面积计算），通过改编信息“绕小路走一圈是50.24米”使本题成为逆向问题（已知圆的周长，求圆的面积），通过增加信息“路宽2米”使本题拓展成为求圆环的面积。一连串的情境围绕主情境分阶段设计，将练习的重点围绕圆和圆环面积的相关知识与经验展开，并逐步地扩展、深入、充实、明晰，既能成为问题产生的源头，又能使整个教学围绕情境产生的问题展开，同时沟通圆的周长相关知识，夯实了学生的基础，调动了学生学习的主动性。

二、情境串变换——关注 “结构化”，提升思维水平

（一）圆环面积变换两圆位置练习

师：要求小路的面积实际上就是求圆环的面积，生活中还见到过哪些圆环？

生：光盘，圆筒形卫生纸，金属垫片……

师：怎么求圆环的面积？（回顾圆环面积计算方法）

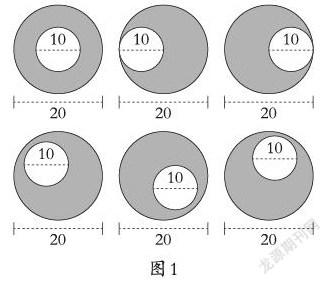
师：（课件随意移动小圆的位置，图1）现在阴影部分的面积怎么计算？

在学生计算完小路面积后，回顾圆环的面积计算方法，即大圆面积减去小圆面积。然后教师利用课件动态演示，帮助学生理解只要是小圆在大圆里面，求阴影部分的面积都可以用大圆面积减去小圆面积来求。这样围绕学生自主生成思维链来设计问题串情境，完善了学生的思维结构，使学生的逻辑思维水平进一步得到提升。

（二）圆环面积变换——一圆一方练习

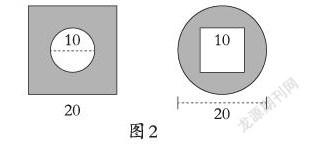
师：如果把其中一个圆变成了正方形，会出现几种新情况呢？

学生独立思考后，教师通过课件动态演示，移走大圆或移走小圆，形成新的图形（图2），学生根据所给信息计算阴影部分面积。

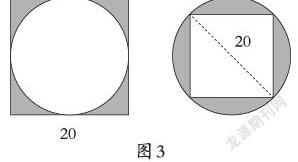
学生计算出两个图形阴影部分面积后，观察发现都可以用大面积减去小面积来计算，教师继续课件动态演示，把圆的直径变成和正方形的边长或对角线相等。（图3）思考：和刚才的图形比较，有什么相同和不同的地方？这两个图形变成了哪两种特殊图形？求阴影部分面积还可以怎么求？教师巧妙改变圆的大小引出外方内圆和外圆内方，通过提问：同样直径是20厘米，为什么第一个图是0.86r2，而第二个图是1.14r2？进一步理解掌握求阴影部分面积的特殊情况，沟通了知识间的内在联系，帮助学生形成结构化思维。

在教学中，教师通过对真实的情境进行几次不同的变换，持续提炼出丝丝入扣的问题串，让学生沿着问题层层深入思考，把零散的思绪、灵感、知识、技能，以及其他各种信息用一种框架收拢起来，逐步将数学知识结构化，从而获得知识与方法。

三、情境串延伸——关注 “综合性”，拓展思维空间

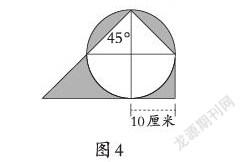
师：如果外圆内方这个图形再变一变（图4），你还会求阴影部分的面积吗？你有什么好办法？

在学生充分交流基础上，教师课件动态演示添辅助线，同时把上面两个阴影对折翻下来（图5），现在可以怎么来求阴影部分的面积？可以运用哪些方法来计算？在学生独立完成后再让学生分别说一说是怎么求的？并展示学生的两种方法（图6、图7）。

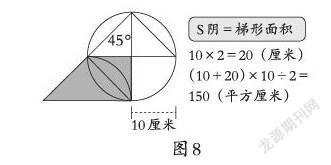
在交流完两种方法后，引导学生继续思考：还能再割补吗？你还想到了什么？在学生讨论基础上，教师课件动态演示把右边的小三角形旋转到左边，形成一个梯形，现在可以怎么来求这个阴影部分面积？你是怎么计算的？展示学生方法（图8）。通过这题的解答，你又有什么新的体会？

在交流总结中引导学生发现，阴影部分的面积一般可以用整个图形的面积减去空白的面积。但有时候通过分割、旋转、拼凑等方法也可以将各个部分的面积相加，或者直接求出所拼成的基本图形的面积。这样一组图形的分割策略的递进，把复杂问题简单化，使解题的策略更加开放、综合，学生获得了更多的分析机会，思维得到更宽阔的拓展，同时可以兼顾到不同层次的学生关注细节，获得成功体验。

练习课引进情境串练习，从一个主问题出发引出若干子问题，这些问题层层递进、环环相扣，相互关联，彰显练习题之间的系统性和整体性。同时，把这些情境作为支撑和激励学生学习的源泉，可以让学生充分暴露思考的方法和过程，从整体上把握知识，构建认知结构，从而有效促进深度学习，促成学生的理解，提升学生的数学素养。

参考文献

[1]叶婉贞.情境串练习：“思”“趣”结合，“比”“变”提升[J].小学数学教师，2021（04）.

[2]刘仍轩.基于教材提升学生数学素养[J].小学数学教师，2017（04）.

[3]吴正宪.从“情境串教学法”到“数学建模”[J].小学数学教师，2017（04）.

[4]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.