终端角度约束制导及制导控制一体化方法综述

赵 斌，梁乐成，蒋瑞民，周 军

(西北工业大学精确制导与控制研究所，西安 710072)

0 引 言

制导武器对坦克、舰船等高防护等级目标精确打击时，制导系统除满足打击精度要求外，往往还需实现对目标的大落角/垂直侵彻打击。在战斗部威力不变和末速度变化较小的前提下，增强毁伤效果、充分发挥制导武器打击效能。

大落角/垂直打击本质上属于飞行器终端弹道角度约束问题，可通过设计终端角度约束的制导方法或制导控制一体化方法实现。

1)终端角度约束制导方法由Kim等首次提出，目前已经发展出多种解决方案：① 基于比例导引的方法，如偏置比例导引、多相复合比例导引等；② 基于现代控制理论的制导方法，如最优控制、变结构控制、自适应控制等；③ 基于几何曲线、优化理论等其他类型制导方法。

2)传统的频谱分离假设在诸如飞行器高速高动态下压打击等特殊场景下并不满足，从而会导致制导控制系统性能严重下降甚至失稳。为充分利用制导与控制回路的耦合关系和挖掘系统潜能，一种新的设计思路是基于制导控制一体化设计实现终端角度约束。制导控制一体化方法由Williams等提出，目前发展出变结构控制、自适应控制、反演/动态面控制、反馈线性化等设计方法。

开展终端角度约束制导及制导控制一体化研究时，多数方法假定系统各环节理想工作，并忽略相关物理约束。然而，导引头视场角范围、弹体最大可用过载以及自动驾驶仪的动态特性等都存在一定约束范围。此外，系统还存在未建模动态、气动参数扰动和目标机动等多种不确定性，以及被控对象模型简化、解耦和线性化时引入的系统不确定等问题。这些因素是制导控制系统设计时必须考虑的问题。

本文系统梳理了终端角度约束的制导方法和制导控制一体化方法的研究现状。首先，分析了典型终端角度约束的定义，建立了面向终端角度约束制导及制导控制一体化设计的状态空间模型；其次，针对终端角度约束制导问题，综述了以滑模变结构、比例导引、最优控制等为代表的落角控制制导方法；第三，针对终端角度约束的制导控制一体化问题，综述了滑模变结构、反演法/动态面、自适应理论、反馈线性化等设计方法；最后，针对终端角度约束制导方法和制导控制一体化方法存在的问题和发展趋势进行了分析与展望。

1 问题描述

本节给出终端约束角度定义，建立了终端角度约束制导及制导控制一体化设计的状态空间模型。

1.1 终端约束角度的定义

终端角度约束制导方法中关于终端角度的定义有三种：弹道倾角、弹目视线角和弹目相对速度夹角。对于防空反导等高动态场景，常通过对弹目相对速度夹角的控制实现对目标的逆轨拦截。本文主要研究对地/海打击静止或低速运动目标场景，则可通过控制终端弹道倾角实现大落角弹道，由于终端视线角与终端弹道倾角之间存在一一对应关系，因此可等效为对终端视线角的控制。

弹目视线角是导引头光轴与弹目视线的夹角。如导引头框架跟踪回路动态特性良好，则弹目视线高低角可近似为攻角与前置角之和。目前制导律文献通常假设飞行器具有小攻角，进而用前置角近似弹目视线角，其本质是在建模时忽略了弹体姿态。

1.2 终端角度约束制导问题描述

1)纵向平面终端角度约束制导问题描述

图1为纵向平面对地/海攻击弹目相对运动示意图，,分别为导弹和目标质心；和分别为惯性系和视线系；,是弹目相对距离和视线高低角；,分别为导弹和目标速度，对地/海打击时有≫；,分别是导弹法向加速度和弹道倾角；导弹前置角=-。

根据图1所示的弹目相对几何关系，可得：

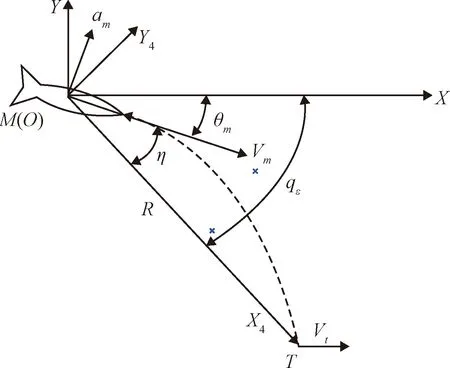
图1 纵向平面弹目相对运动Fig.1 Missile-target relative movement in longitudinal plane

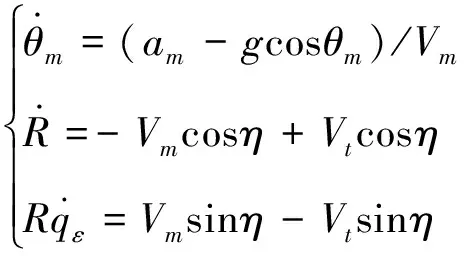
(1)

对式(1)微分化简，可得弹目相对运动模型：

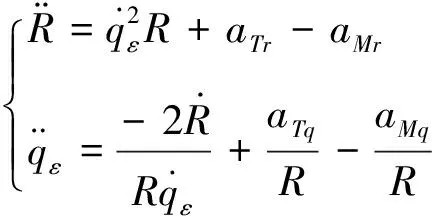
(2)

其中，(,)和(,)分别是目标及导弹沿视线方向和视线法向的加速度分量。

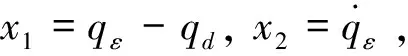
(3)

其中，为由目标加速度引起的有界未知不确定性。

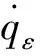
2)三维终端角度约束制导问题描述

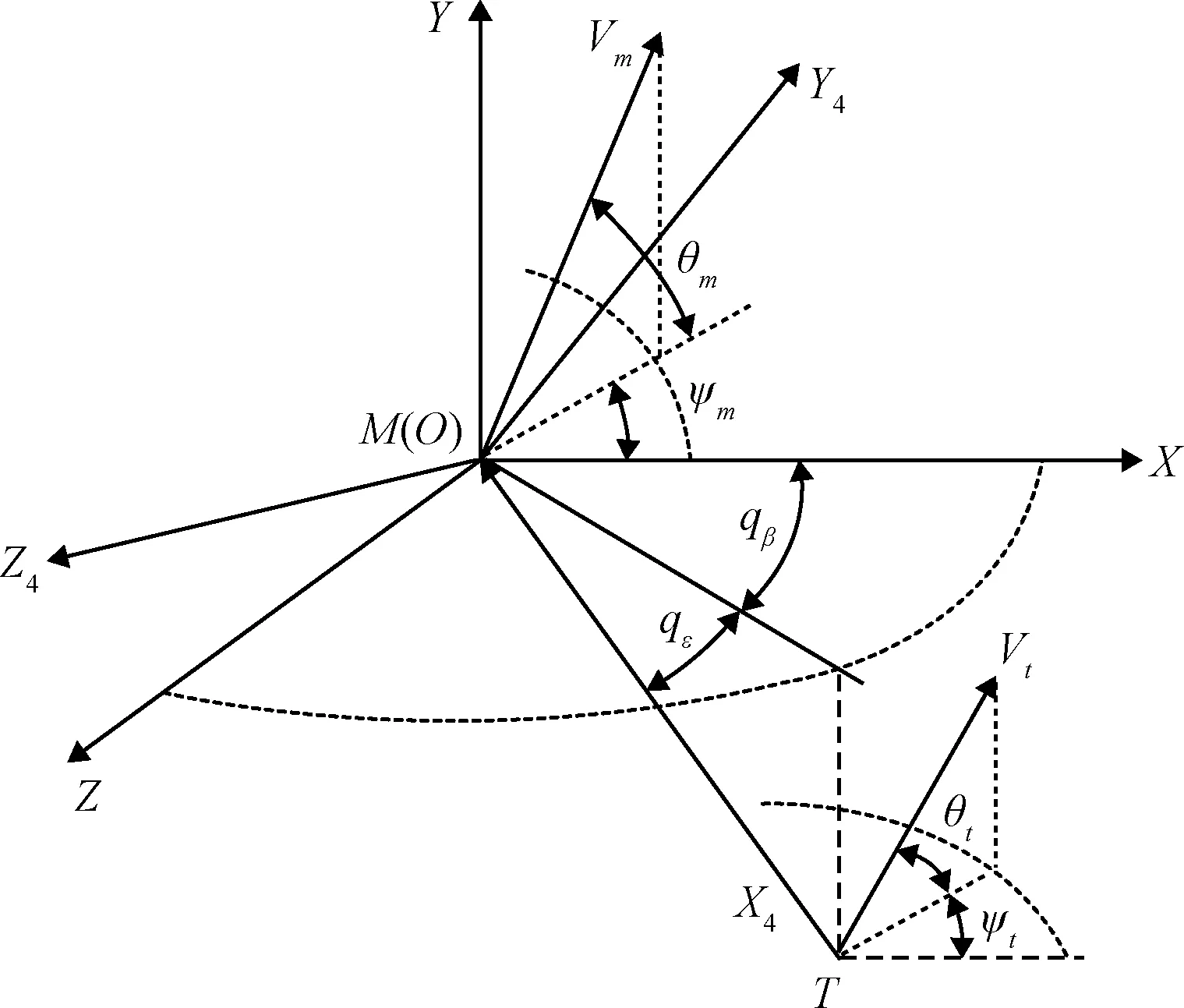
图2 三维弹目相对运动Fig.2 Missile-target relative movement in 3D space

图2为三维弹目相对运动示意图，,分别为导弹和目标质心；和分别是惯性系和视线系；,,分别为弹目相对距离、视线高低角和视线方位角；,分别为导弹和目标速度，满足≫；,是导弹弹道倾角和弹道偏角；,是目标弹道倾角和弹道偏角。根据图2可得：

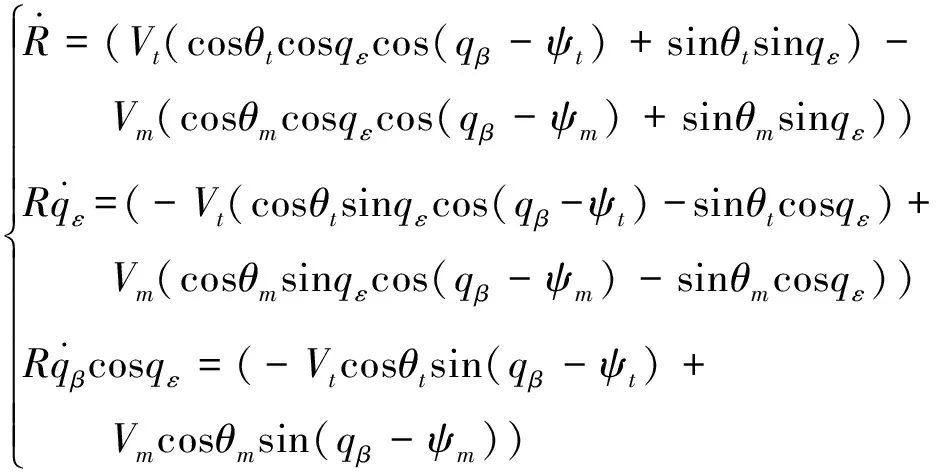
(4)

对式(4)求导，可得三维相对运动模型：

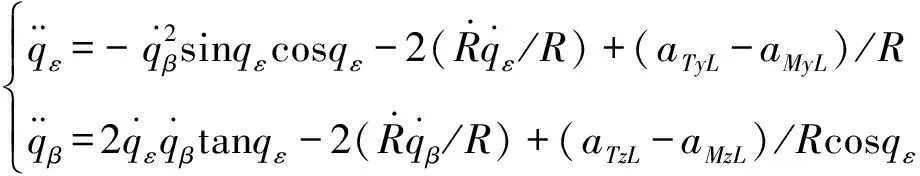
(5)

式中:(,)和(,)分别为目标和导弹在视线坐标系沿视线法向的加速度分量。

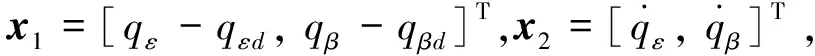
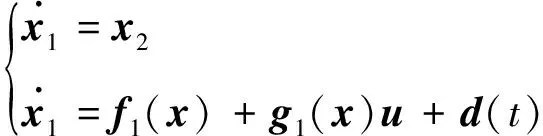
(6)

(7)

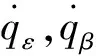
1.3 终端角度约束制导控制一体化问题描述

本节建立面向终端角度约束的制导控制一体化设计模型，给出设计目标。

1)纵向终端角度约束一体化设计问题描述

如图1所示场景，由式(2)纵向平面弹目相对运动方程，结合导弹姿态动力学和运动学方程可得：

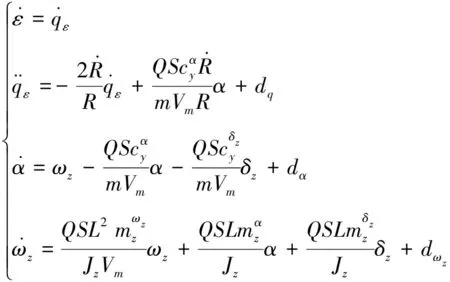
(8)

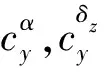
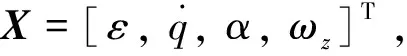
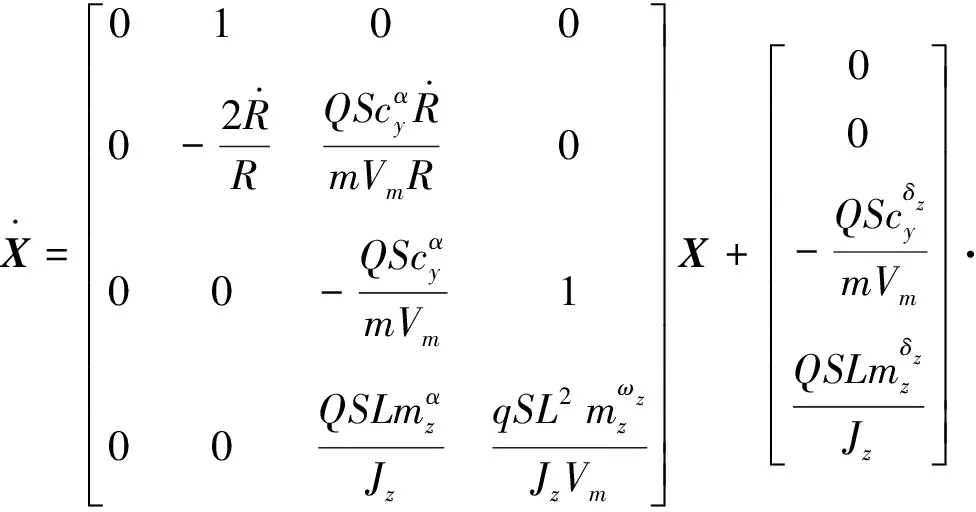
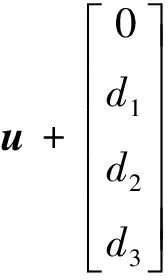
(9)

通常对于姿态稳定飞行的导弹，攻角、舵偏角、角速度和气动参数摄动均有界，即||≤,=1,2,3,为不确定性上界。若考虑执行器饱和特性，则一般采用平滑后的饱和函数()代替输入。

纵向平面终端角度约束制导控制一体化的目标是设计控制律使系统有界稳定，终端落角误差和视线角速率均趋于零。若考虑视场角和过载约束，则∀∈[0,]，满足|()|≤，|()|≤,,分别为可用的最大视场角和最大舵偏角。

2)三维终端角度约束一体化设计问题描述

如图2所示的场景，由式(5)弹目相对运动方程，结合导弹姿态动力学和运动学方程，可建立三维终端角度约束制导控制一体化模型，限于篇幅，这里略去建模过程。

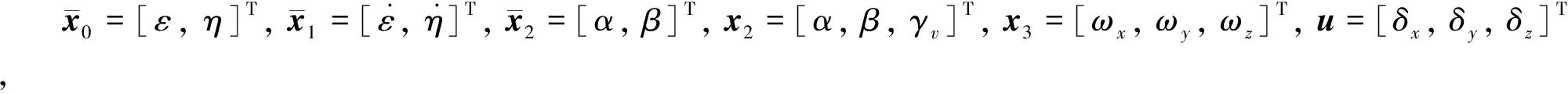
(10)

其中，各变量定义如下：

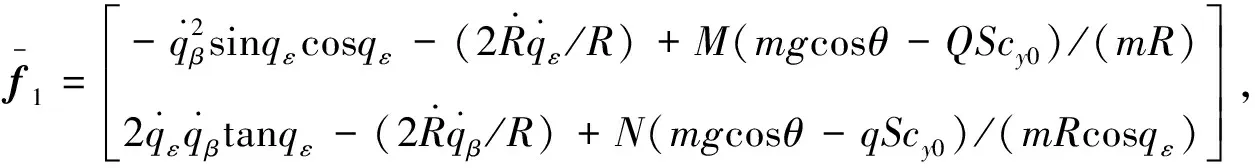
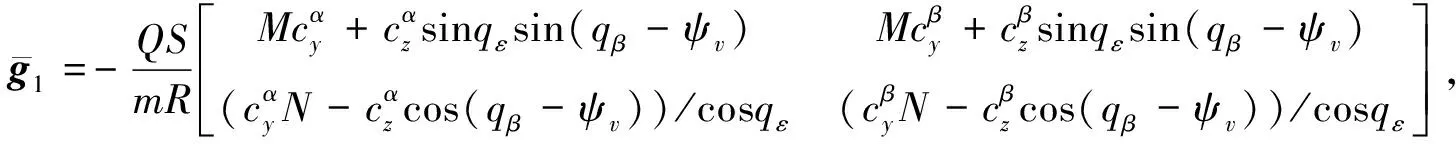
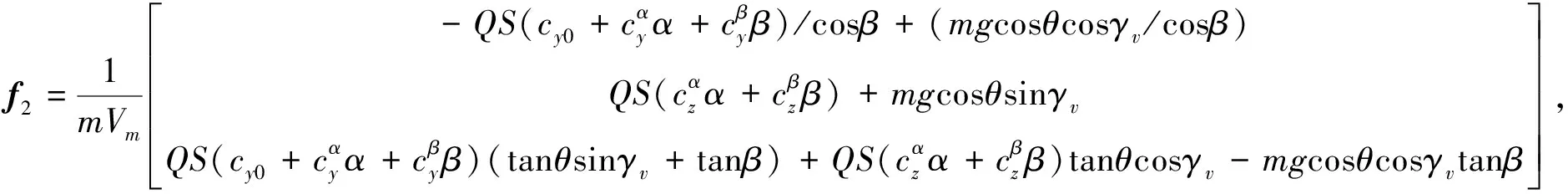
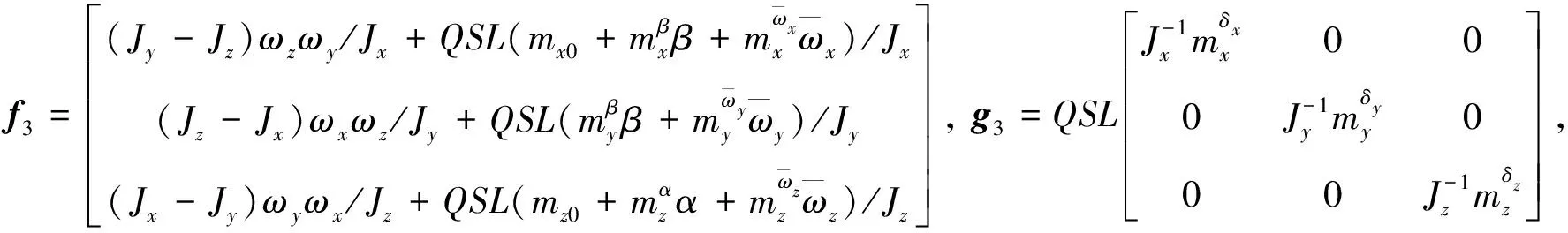
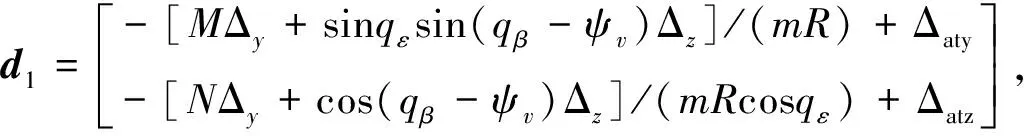
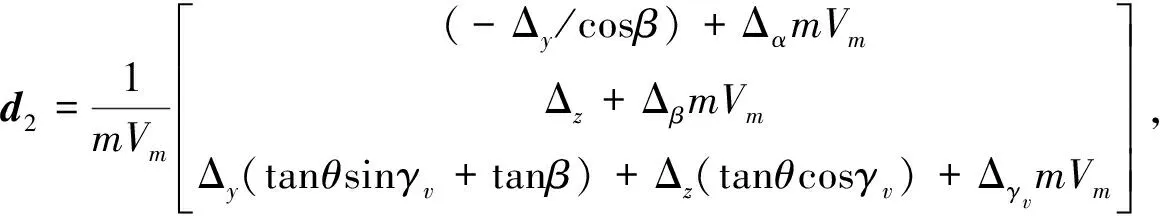
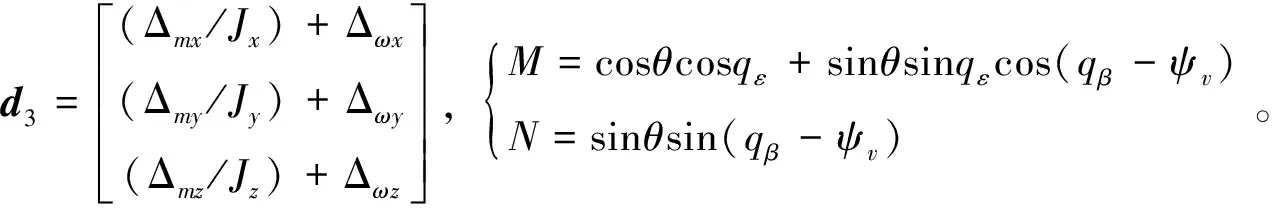
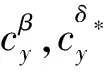
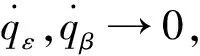
2 终端角度约束制导方法综述

针对终端角度约束的制导设计方法主要包括滑模变结构方法、比例导引及其改进方法和最优制导相关方法。

2.1 基于滑模变结构的设计方法

带角度约束的滑模制导方法由Kim等首次提出，以纵向平面制导为例说明其设计思路。

针对式(3)所示的状态空间模型，选择滑模面：

=+

(11)

并且设计自适应滑模趋近律为：

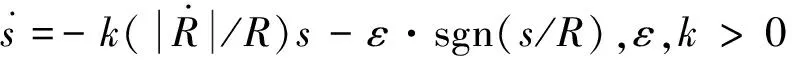
(12)

对式(11)求导，结合式(12)，可得滑模制导律

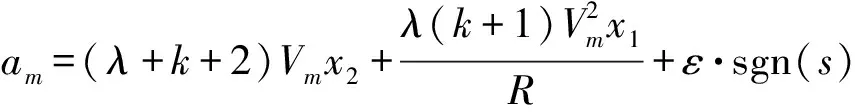
(13)

显然，式(13)不连续，这是滑模控制的显著特点，一般选取平滑函数近似sgn()缓解抖振。

1) 有限时间收敛滑模制导方法

通常末制导时间有限，只有视线角速度在交会前收敛至零才能实现准平行接近。因此，有限时间制导引起了广泛关注。

Zhang等基于有限时间稳定理论和终端滑模方法设计了落角约束的滑模制导律，在有限时间内零化视线角速率和落角误差，由于制导律中含有状态负指数项，当状态趋零时不可避免会产生奇异问题。为此，Lin等提出了满足落角约束的非奇异有限时间制导律，在状态趋零时实现从终端滑模到线性滑模的切换，同时设计二阶状态观测器对目标机动进行估计与补偿。这种切换思想有效避免了奇异问题，但随之带来的指令跳变不利于控制系统跟踪。Zhao等提出了基于全局滑模的有限时间制导律，避免使用切换逻辑且指令光滑，可实现对运动目标的全向拦截。有限时间制导的关键是收敛时间估计，其通常随初始条件变化，实际系统对初始条件的测量误差可能导致稳定条件的不可达。因此，快速收敛制导律也得到广泛关注，Sun等提出了一种带落角约束的快速终端滑模制导律，能够优化拦截轨迹的同时有效缩短拦截时间。

2) 多约束滑模制导方法

在设计终端角度约束制导律时考虑自动驾驶仪动态特性、物理约束等工程因素是当前的研究热点。部分学者将自动驾驶仪特性近似为一阶环节，这实际上无法准确反映其高阶动态特性。Xu等基于快速终端滑模提出了考虑自动驾驶仪二阶动态特性和落角约束的有限时间制导律，能够有效补偿自动驾驶仪的动力学滞后。这类方法能较好地反映实际自动驾驶仪的特性，但其需要获取导弹加速度及其导数等信息。Zhao等采用滑模观测器估计切向相对速度及其导数与集总扰动信息，基于动态终端滑模设计了连续制导律，有效避免了抖振问题，该方法的优点是在考虑驾驶仪动态特性时只用了相对速度信息。

对于考虑视场角约束的制导问题，第1种解决方案是采用多阶段切换的制导策略，切换会造成指令突变，在制导末段可能导致较大误差。典型思路是设计两种制导律，分别用来保证落角约束和视场角恒定，当接近视场角约束边界时切换为恒定视场角制导律并保持。He等提出的落角约束制导律能够在导引头最大视场角下保持长飞行时间，由此获得较大的落角范围，更易实现大落角约束打击。第2种思路是将导引头视线角视为系统状态，采用状态约束控制理论设计制导律，保证视场角约束得到满足，也可以扩展到考虑过载约束的情形。Wang等采用积分型障碍Lyapunov函数设计趋近律，通过时变滑模面保证闭环系统的有限时间收敛。这类方法不涉及切换逻辑，制导指令连续，Zhou等在研究变速导弹约束问题时，同样使用了这类思想。

3) 三维滑模制导律

大量文献尝试将成熟的二维落角约束制导律扩展到三维场景，进一步提高制导效果。Si等基于非奇异终端滑模控制设计了三维制导律，但其只考虑了静止目标情况；更进一步，Gao等提出了固定时间收敛的三维落角约束滑模制导律，能够实现对运动目标的有效拦截；针对机动目标拦截问题，史绍琨等基于非奇异快速终端滑模面和二阶滑模控制理论，设计了带落角约束的三维滑模制导律；Zhao等也采用了类似方法进行制导律设计。

2.2 基于比例导引及其改进的设计方法

比例导引形式简单、容易实现，是广泛应用的制导方法，但其无法直接保证落角约束，尤其是大落角弹道。控制落角最直接的设计思路是进行指令补偿，例如在制导律中合理引入重力补偿，可使初段弹道抬起而末段弹道回拉。然而，该方法对于增大实际落角效果有限，且落角误差难以控制。为了实现对目标的大落角打击，对比例导引的主要改进方向是偏置比例导引和多相复合比例导引。

1)偏置比例导引方法

通过偏置项控制期望落角最早由Kim等提出的，其存在剩余时间等信息难以准确估计的问题。

简要说明其设计思路，对图1所示纵向平面拦截问题，带时变偏置项的制导律可设计为：

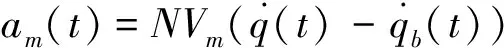
(14)

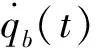
为满足大落角约束要求，设计时变偏置量

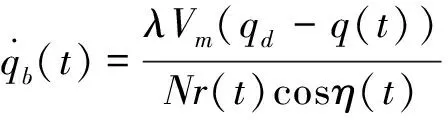
(15)

式中:为任意正常数。在制导过程中还要满足

|()|<,>1+cos(),>0

(16)

分别对应视场角约束和导航比要求。

偏置比例导引相关文献常采用小角度线性化假设模型，导致其难以处理目标机动问题，并且有效发射区过于狭窄；Akhil等基于非线性动力学设计了改进的偏置比例导引律，针对机动目标实现了大范围的落角约束；Zhang等设计了基于前置角余弦项的制导律，推导了剩余时间的递归估计方法，实现了全向落角控制，但没有考虑各种约束问题。

偏置比例导引方法的灵活性在于可以通过选择不同的偏置项来满足不同约束条件。为满足视场角约束并适应速度时变情况，Kim等设计偏置项使视线角保持在有界区间内，并将自变量改进为弹目相对距离的函数，保证了非匀速假设下末端状态的收敛；在三维场景下，Park等提出基于四元数的落角约束偏置导引律，实现了全向目标的精确打击。

2)多相复合制导方法

多相复合制导的思路是针对全弹道多个制导阶段分别设计制导律及其切换策略：(1)不同比例系数切换；(2)纯比例导引和偏置比例导引间切换。

对于前者，为了克服传统比例导引在≥2时可达落角范围有限的问题，Ratnoo等提出两阶段的复合制导方法，在弹道初始段通过设置<2实现全向0～π落角范围，并在满足切换条件后转换导航比为=2从而实现期望落角。该方法切换条件的选取异常重要，由于测量误差等因素存在，切换时机选择不当容易导致较大误差。对于纯比例导引和偏置比例导引切换的思路，Erer等提出了两阶段复合制导方法，当偏置项的连续时间积分达到设定值后切换为纯比例导引，通过调整临界值间接控制落角；该方法随后被扩展到打击运动目标场景。积分误差积累容易引起这种方法的制导偏差。

3)考虑多约束的比例导引方法

多约束问题是当前比例导引方法的研究热点，一般是基于偏置项设计满足各类约束。针对视场角约束和过载约束问题，Kim等提出了仅依赖于视线角信息的两阶段定常偏置制导律，针对静止目标实现了最大可达落角范围；针对运动目标，Park等提出了含两阶段时变偏置项的制导律，可同时满足视场角及过载饱和约束，两种偏置项分别实现极限过载范围内的落角控制和视场角约束；文献[48]讨论了最大可达落角及导引律增益的选择方法；以上方法都假设导弹飞行速度恒定，Pang等提出了四阶段的时变偏置比例导引法，除视线角及过载约束外，还考虑了气动特性及速度时变特性，对非机动目标具有较强适应性，并且制导指令简单易实现。

2.3 基于最优控制理论的制导方法

最优制导方法理论上具有最优性，并且便于处理各种约束，如能量最少、特定落角等，但其对建模精度要求较高，并且存在剩余时间准确估计难、求解过程复杂、实时性差等问题。本节针对落角约束的最优和次优制导方法，介绍剩余时间估计、最优控制求解等方面的研究进展。

1)最优制导方法设计思路

对式(1)微分，可以得到关系式

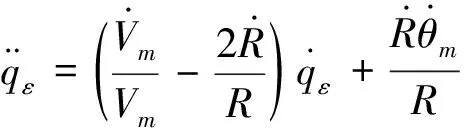
(16)

状态变量及输入选取同式(3)，记≜[,]，则系统状态空间描述为

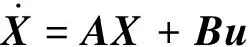
(17)

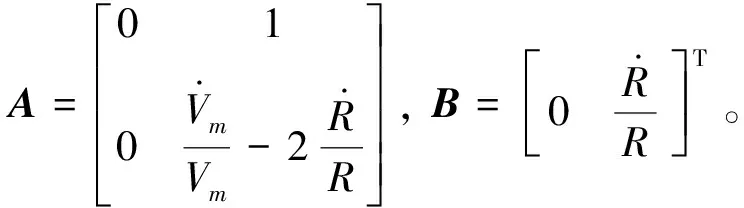
为使空气阻力造成的速度损失最小，同时考虑终端角度约束，可设计二次型性能指标

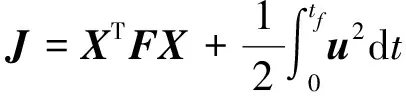
(18)

式中:为加权矩阵。根据最优控制理论可知最优解为：

=-

(20)

式中:=,为以下Riccati方程的解

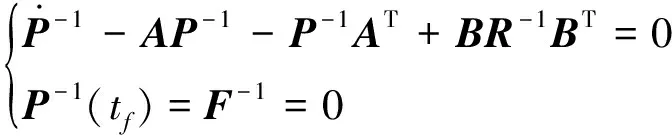
(21)

根据以上各式，可得最优控制量为

(22)

结合弹目相对运动关系，即可得到最优制导律：

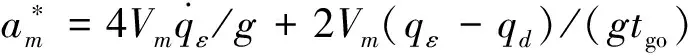
(23)

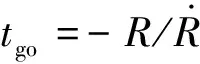
剩余时间估计精度会直接影响制导律的效能，大落角打击时弹道曲率较大，其剩余时间估计更为困难。常用方法主要有以下几种：

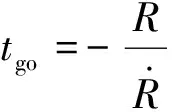
通过在性能指标中引入各种约束，最优制导方法除满足落角约束外，还可满足过载、自动驾驶仪等其他约束。为约束末端加速度并抵消重力影响，Li等设计了幂函数形式的性能指标，通过将控制指令权重设计为剩余时间倒数得到了扩展最优制导律，并估计了最大需用加速度；王辉等设计了考虑驾驶仪动态特性和落角约束的最优制导律；Lee等基于广义加权函数推导了落角控制最优制导律的解析解，考虑了自动驾驶仪动态特性和导弹时变速度等因素，更适合真实导弹模型。

通过设计附加切换逻辑来考虑约束问题也是一种解决方案，具体思路与滑模方法类似。针对捷联导引头视场约束问题，Park等以剩余距离为权重设计了同时满足落角和视线角约束的最优制导律，在初制导段增大视场角到最大、中制导段维持最大视场角、末制导段以期望落角打击目标，并且给出了制导切换逻辑，该方法只考虑了目标静止情况；Wang等通过引入时变的虚拟期望落角来减小过载幅值，其制导参数自适应于不同弹目初始相对距离，能够实现大落角打击弹道。

2)次优制导设计方法

最优控制理论在处理非线性系统时需要求解非线性HJB方程，极小值原理等方法虽求解精度高，但求解过程复杂、实时性差。为简化求解过程又不至于严重损失精度，改进方法主要有：状态依赖Riccati方程(SDRE)方法、-D方法和模型预测静态规划(MPSP)方法。

SDRE方法将非线性方程转化为类线性结构，使用线性最优控制方法进行相关的设计综合，其具有稳定性、最优性和鲁棒性等优点。Zhao等基于SDRE法设计了考虑三阶自动驾驶仪特性的角度约束制导律，在每个求解步骤中涉及一个计算量较小的代数SDRE问题；Parwana等提出了考虑攻角约束的SDRE次优制导律。这类方法由于需要反复求解黎卡提方程，求解效率较低。

-方法将HJB方程转化为一组递归的代数方程并求其近似解，可以保证计算精度。王洪雪等针对BTT导弹设计了带落角约束的三维次优制导律，但其未考虑目标机动及随机干扰因素，鲁棒性有待讨论；Man等针对三维耦合非线性模型提出了基于-法的次优落角约束制导律，通过引入扰动观测器增强系统鲁棒性；相比于SDRE法，-方法引入了和两个参量，只需要在初始时刻求解一次黎卡提方程，即可递归得到闭环的非线性反馈控制律，避免了大量在线计算。

MPSP方法将动态规划问题转化为静态规划问题进行最优求解，本质上是一种结合近似动态规划和模型预测控制的方法，可以实现快速的在线轨迹优化，缓解动态规划计算复杂性等问题。Maity等设计了一种广义模型预测静态规划方法，利用预测量和期望末端输出的误差，以低维权重矩阵反向传播方式实现带终端约束的非线性静态优化问题的快速求解；Mondal等对MPSP进行扩展，将控制量表示为基函数的加权和，将优化过程简化为参数优化问题，进一步降低了问题维数，提高了计算效率和控制的平滑性，基于此推导了带落角约束的三维最优制导律。MPSP方法需要精确的模型信息以实现预测环节，若系统存在未知扰动及未建模动态，预测模块将会导致误差积累甚至求解发散。对此，可以结合滑模方法对其进行改进。

2.4 终端角度约束制导方法的对比分析

表1总结了各种终端角度约束制导方法的优缺点。其中，滑模变结构方法主要优点是强鲁棒性，并且能够实现有限时间收敛、非奇异等多种要求的性能；以偏置比例导引和多相复合比例导引为代表的比例导引方法形式简单并且计算量小，也易于估计其可达落角范围，因此在工程上应用较为广泛，但实际的系统性能有限；最优控制能够在理论上达到最优性能，但存在求解困难的问题，对弹载计算能力有一定要求，不利于实时控制，各类次优制导律则一定程度上缓解了这一问题。

表1 终端角度约束制导方法对比Table 1 Comparison of guidance laws under terminal angle constraints

3 终端角度约束的制导控制一体化方法综述

高性能作战对系统响应提出了更高要求，制导与控制回路的时间常数差逐渐减小，传统设计方法由于频谱分离假设不再满足暴露出一些弊端，导致指令饱和甚至脱靶。制导控制一体化(Integrated guidance and control，IGC)设计逐渐成为研究热点。

3.1 制导控制一体化方法

IGC方法将制导与控制回路看作一个整体进行设计，直接由弹目视线信息和弹体姿态信息得到舵偏指令信息，其在缩短设计周期、降低成本的同时，能有效提高系统综合性能。

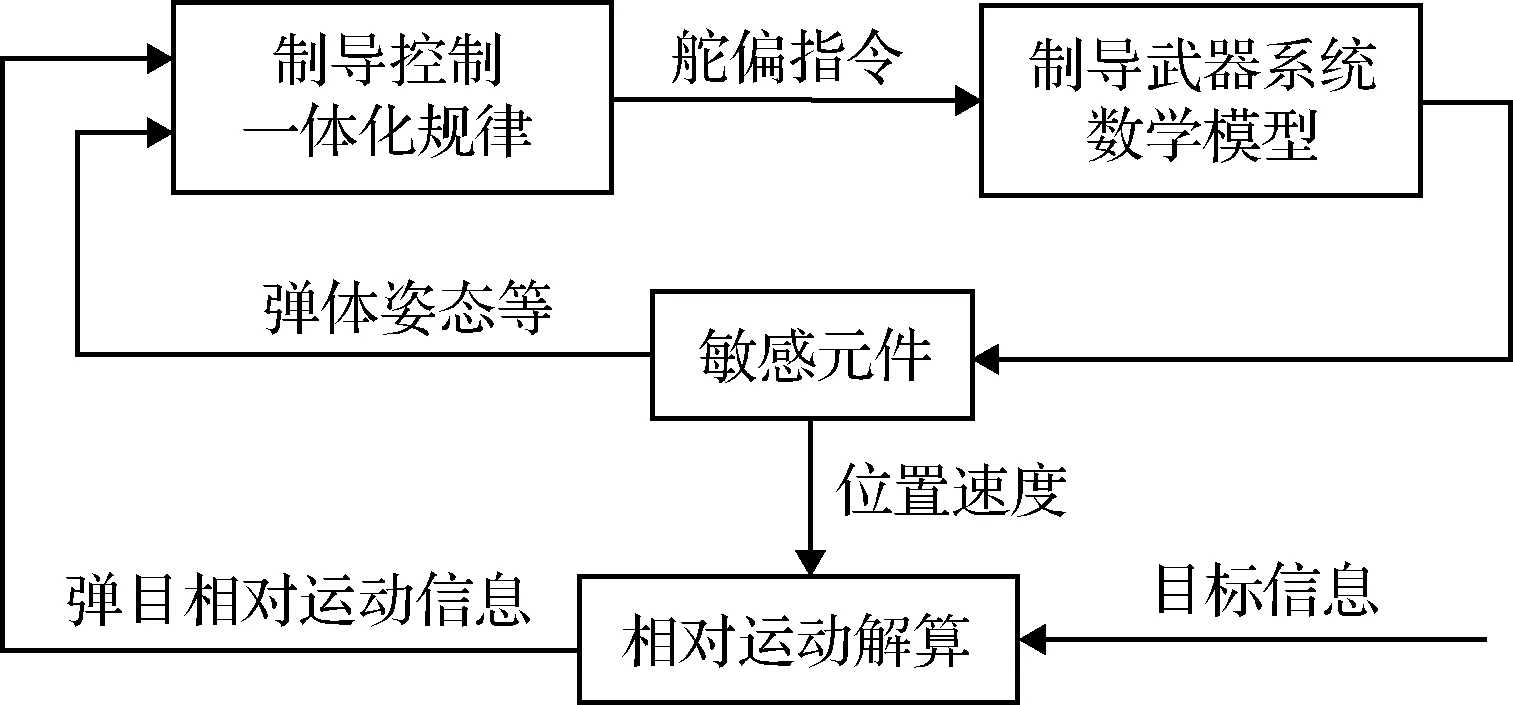
图3 制导控制一体化设计框图Fig.3 Design diagram of the IGC

综合相关文献，自提出以来，IGC方法大致经历了从部分一体化到完全一体化设计的发展历程。

1) 部分一体化设计

如图4所示，部分一体化设计采用双环控制器结构，其结合了制导控制分离设计和完全一体化设计的优点，外环控制器基于各回路协调关系产生弹体角速率虚拟指令，内环控制器产生舵偏角指令。相比完全一体化设计其降低了设计难度，并实现了各回路在一定程度上的集成设计，但其本质上是对传统方法的部分改进，未能充分挖掘系统潜能。

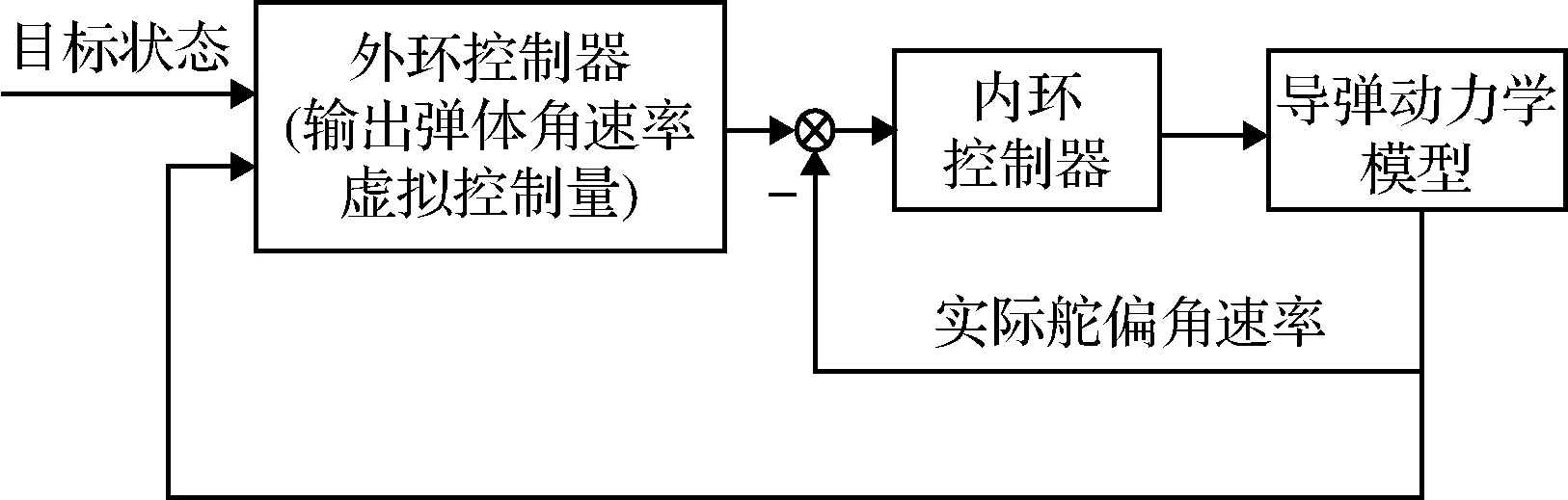
图4 部分制导控制一体化设计Fig.4 Partial integrated guidance and control design

2) 完全一体化设计

如图5所示，完全一体化设计是将制导回路和控制回路作为整体进行综合设计，其充分利用了各回路之间的耦合关系直接设计一体化规律，更加紧密地综合了制导与控制回路，有利于提高综合性能。

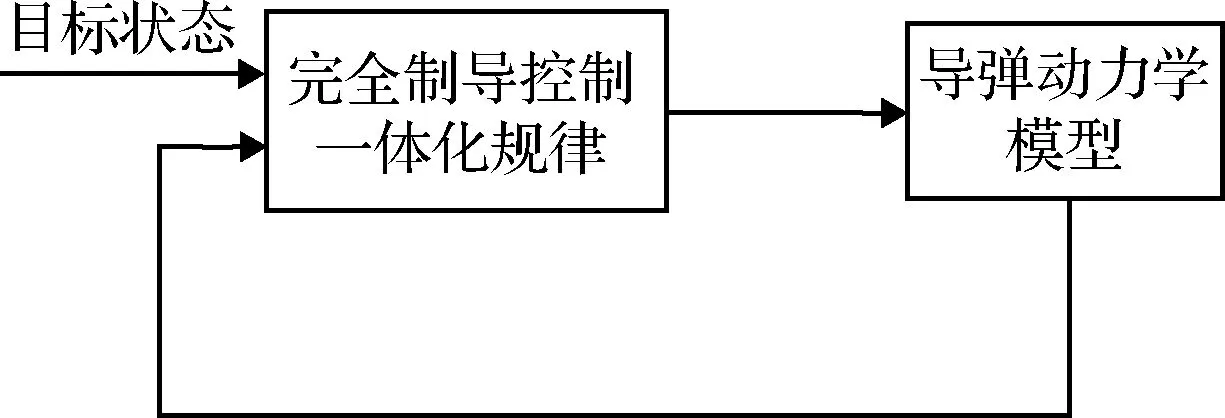
图5 完全制导控制一体化设计Fig.5 Total integrated guidance and control design

这种方法通常有分通道一体化设计和全状态耦合一体化设计两种途径。由于其综合考虑制导系统与控制系统的耦合，通常系统阶数大幅增加，状态变量间存在更为复杂的耦合，同时存在非匹配不确定性，这些因素增大了系统设计难度。

3.2 终端角度约束制导控制一体化设计研究现状

总体来看，IGC设计方法已经存在大量成果，但仍处于研究的早期阶段，距离工程应用还存在一些亟待解决的问题。目前，常用设计方法有滑模控制、反演/动态面控制、自适应控制、反馈线性化等。

1)基于滑模控制的IGC方法

滑模控制本质上是一种非线性控制方法，主要包括滑模面及趋近律两部分设计。以往主要采用二阶或高阶滑模设计IGC规律，高阶滑模相较于二阶滑模能够提高系统精度，但计算负载大；Zhang等基于终端滑模和动态面方法设计了非奇异IGC方法，实现了对静止目标的终端落角控制。

针对模型不确定性、外部扰动等问题，基于干扰观测器的IGC方法是当前普遍采用的设计思路，它能在减弱系统抖振的同时提高对机动目标的打击效果。Chao等将扩展状态观测器引入滑模IGC设计中，采用非线性跟踪微分器估计虚拟指令的平滑导数，同时基于障碍函数实现导引头视场角约束；Fu等设计了有限时间的落角约束IGC方法，利用Nussbaum函数处理执行器饱和问题，并基于改进的有限时间收敛状态观测器来处理系统不确定性。

2) 基于反演法/动态面的IGC方法

反演法将复杂系统分解为低阶子系统，通过对各子系统设计Lyapunov函数和虚拟控制量，并一直“后退”到系统控制量，最终实现控制器设计。该方法能实现系统全局稳定，能处理非匹配不确定问题，但由于计算虚拟控制的高阶导数，容易引起“微分爆炸”问题。Bo等基于反演法设计了满足落角约束的自适应IGC方法，该方法未考虑“微分爆炸”问题具有较高的计算复杂性。部分文献研究了避免“微分爆炸”问题的方法，Ai等通过固定时间微分器估计虚拟控制导数，有效避免了“微分爆炸”问题，在此基础上提出了考虑执行机构饱和与落角约束的反演IGC方法。

建模精度对反演控制效果影响明显，为提高算法的鲁棒性，结合滑模方法的反演控制IGC是普遍的设计方案。基于经典线性滑模，张金鹏等将一体化设计问题转化为系统输出跟踪问题，设计了拦截弹纵向通道的滑模反演一体化控制算法；为进一步提高制导精度，还有学者在IGC设计中引入高阶滑模观测器，这进一步增加了计算量。

动态面由Swaroop等于1997年提出，通过引入一阶滤波器避免反步法中对虚拟指令的直接微分，从而一定程度解决“微分爆炸”问题；该方法需在线估计不确定性或其上界，估计精度很大程度影响控制精度。Hou等将IGC的设计问题转化为不确定性时变非线性系统的状态调节问题，基于自适应扩展动态面法设计了落角约束的IGC方法。

基于动态面的IGC设计中考虑各种物理约束问题也受到了广泛研究。针对执行机构饱和及失效问题，Wang等通过线性扩展状态观测器估计执行器故障等引起的模型不确定，利用平滑正切函数、Nussbaum函数和辅助系统补偿输入约束，基于动态面设计了三维IGC规律，实现了对静止目标打击的终端落角控制；此外，障碍函数也被用于解决多约束问题，Tian等针对时变速度和捷联探测下的IGC设计问题，通过将导引头视场角约束等价转化为对弹目视线法向速度分量的时变约束，基于障碍Lyapunov函数设计了IGC规律，在实现了弹目视线角速度趋零的同时，还满足了时变非对称约束。

3)基于自适应理论的IGC方法

自适应控制可以根据系统状态动态调整控制参数从而降低系统不确定性对控制效果的影响。文献资料显示该方法通常与其他方法相结合进行应用。

Wang等针对严格反馈的三维耦合制导控制一体化模型，结合动态面法和自适应控制设计了带落角约束的IGC规律，并同时满足了执行器饱和约束，该方法未考虑模型不确定性；Liu等针对落角约束的三维IGC设计问题，采用严格反馈形式的自适应控制来处理气动系数和惯性矩引起的不确定性，进一步扩展了应用范围；赵晨东等将反演控制与自适应控制相结合，针对一体化模型存在的未知有界不确定性特点，设计了俯仰平面内带落角约束的自适应IGC规律，能够打击地面各类机动目标。

4)基于反馈线性化的IGC方法

反馈线性化将非线性系统通过状态反馈方式转化为线性动态系统，本质上是一种处理非线性问题的方法，由于转化过程中仍然保留系统的高阶分量，从而保证系统的等价性。周觐等采用反馈线性化方法，将俯仰平面IGC模型转为可控线性模型，并结合自适应控制及反演控制设计了IGC规律，但其未考虑系统不确定性。反馈线性化对精确建模要求较高，不具备对参数及模型不确定的鲁棒性，不利于工程实际应用。对于IGC系统中存在的不确定性，可通过干扰观测与补偿方法解决。尹永鑫等提出了基于动态逆的反馈线性化IGC规律，为提高系统鲁棒性，采用扩张状态观测器对模型误差和未知扰动进行观测，该方法未考虑执行机构特性等的影响。

表2 终端角度约束制导控制一体化方法对比Table 2 Comparison of IGC laws under terminal angle constraints

3.3 终端角度约束一体化设计方法的对比分析

表2总结了各类大落角约束IGC方法的优缺点。其中以滑模控制和反演/动态法最为常见，滑模控制方法的强鲁棒性是其主要优点，但非匹配不确定性估计问题和抖振问题制约了其进一步的发展，反演/动态面法适用于具有严格反馈形式的系统，并且性能依赖于建模精度。因此，大量文献结合滑模控制和反演方法的优点来设计控制方法。另外，自适应控制通常结合其他方法来提升控制性能，而反馈线性化能够大幅度降低设计难度，但有待于进一步降低对精确建模的依赖程度。

4 终端角度约束制导/制导控制一体化技术展望

目前，国内外针对大落角约束制导和IGC均开展了系统性研究，相关方法在一定前提和假设下能有效提升制导控制系统性能。然而，从工程应用和理论探索角度看，还有一些问题亟待研究。

4.1 终端角度约束制导技术展望

由于引入了相关假设前提，以垂直打击为代表的大落角约束制导方法大多仅停留在理论层面，距离实际应用尚有距离，总结下来有如下几个问题：

1)信息估计与制导协同设计问题

为了解决落角约束、输入约束、视场角约束等复杂问题，国内外学者提出了诸多制导方法，综合来看这些方法形式复杂，并且部分制导信息难以准确测量，制约了其工程应用。这种问题在最优制导方法中尤其明显，不仅增大了系统测量和优化的难度，而且增大了实时制导和控制系统跟踪指令的难度。一般情况下，导引系统能够准确测量和估计的信息有弹目视线角及其角速率，惯导设备能提供质心位置及速度等信息，而现有部分大落角约束制导律中还需要用到弹目相对距离及其高阶导数、剩余时间等难以准确测量和估计的制导参数。

解决该问题的思路有两个：①改进现有形式简单、参数易估计的比例导引方法，进一步挖掘其实现复杂任务的潜能，如多阶段切换或偏执比例导引等；②开展制导律与信息估计的协同设计，即在设计制导规律时考虑对制导信息误差的鲁棒性，同时将制导规律产生的运动趋势信息引入状态信息估计中，并且综合进行制导与估计过程的优化设计，从而在满足制导效能的前提下实现制导信息的估计。

2)状态/输入约束及速度时变下的大落角控制

近年来，输入约束、视场角约束和自动驾驶仪等多约束制导理论方面涌现了大量研究成果。然而，大多数方法仅针对个别约束存在的情况开展研究，鲜有考虑全部约束的情况；然而，实际制导过程中存在的约束情况远比这些简单约束要复杂，导弹速度时变、终端速度约束、部分状态约束等问题同样具有实际意义。以导弹恒速推导出的快速收敛制导律用于变速导弹时，制导增益通常针对速度上界选取，造成了参数保守性，且速度上界通常也难以估计；制导过程的导弹末速控制很重要，末速过大会导致不满足动压、热流等约束，末速过小则会影响毁伤效果且容易被敌方防御系统拦截。因此，制导方法设计时应尽可能避免不必要的假设简化，并且尽可能考虑更多工程实际约束。从这个角度看，现有研究还需要进一步深化。

3)落角约束的可达范围估计与优化

导弹发射初始条件会影响落角范围，为了更好地为发射条件设计提供理论指导，有必要从理论层面对落角可达范围进行准确估计。导引头视场角、侧向过载等约束会对落角范围产生影响，导致无法实现大落角打击，甚至系统不稳定，这本质上是闭环系统稳定域的估计与优化问题。制导律的可达落角范围估计是较为复杂的数学问题，文献[99-100]给出了复合比例制导律的稳定域分析，同时在推导可达落角范围时考虑了导引头视场角和过载约束。除此之外，其他类型制导方法由于设计方法复杂，往往导致其落角约束范围解析估计问题鲜有成果发表。这已成为该研究领域的亟待解决的问题。

4) 大落角约束下的多弹协同制导问题

反导技术的发展增大了武器突防难度，因此多弹协同制导技术得到了长足发展。目前主要有隐式方法和显式方法两种形式，隐式协同不涉及多弹通讯问题，容易实现，但在发射时难以合理设置飞行时间；显示协同能够通过信息共享实现弹群协同，更容易实现饱和攻击。

多弹协同下的大落角打击要求同时满足时间约束和角度约束。为满足时间约束，多数方法需要对剩余时间进行精确估计，基于协同机制补偿多弹剩余时间差；然而，大落角弹道往往剩余时间难以估计，并且较大的弹道曲率容易使目标超出导引头视场范围从而影响制导精度。基于数值优化的方式调整制导参数可以降低对剩余时间估计精度的要求，但其数值计算量较大。为此，设计不包含时间信息的协同制导律是重要的研究方向。此外，目前的多弹协同制导大都是针对二维平面设计的，并且考虑导引头视场角约束、过载约束等多约束的协同制导大都局限于隐式协同层面，未能充分利用弹群信息交互提升协同效果，因此考虑多约束条件的三维显式协同制导律也是一个重要研究方向。总之，大落角约束下的多弹协同制导技术目前仍处于早期研究阶段，这将是今后的重要研究方向。

4.2 终端角度约束制导控制一体化技术展望

系统的高阶性、强耦合性和不确定性，使得IGC设计相比制导律设计更为困难。本节对典型设计问题和发展趋势进行展望。

1)考虑多约束的大落角IGC设计问题

对于大落角/垂直打击这类弹道较为弯曲的场景和防空反导等高动态交战场景，工程中最基本的约束包括导引头视角、执行器饱和及故障等。此外，对于特殊的超燃冲压发动机的工作特性，还需要考虑攻角、侧滑角、速度滚转角和弹体转动角速度等状态约束。目前考虑多约束的IGC设计仍然存在诸多问题，例如，视场角约束大都基于小攻角的假设，然而实际大落角/垂直打击是主要通过姿态调整来实现，在导弹机动情况下很可能并不成立，该假设很明显将降低系统控制性能；另外，对于全捷联导弹而言，其制导与控制系统强烈耦合，对其进行IGC设计是一种自然而然的方案。此类导引头的视线角一般为体视线角，但是目前多数IGC方法在视场角建模时忽略导弹的攻角和侧滑角，因此即便满足所谓的“导引头视场约束”，仍然可能导致全捷联导引头对目标跟踪失败，全捷联下的视场角约束仍需要不断改进。

针对输入约束问题常采用Nussbaum函数法，但这类方法在输入指令无穷时才输出最大舵偏，这本质上限制了执行机构能力的发挥，因此有待于进一步改进。对于状态约束问题，部分研究基于障碍Lyapunov函数能在理论层面上对系统状态作严格限制，但这需要导弹在进入末制导段前状态就满足要求的初始条件，并且要求飞行器具有良好的控制能力，否则对状态的严格约束将无效。

2)非严格反馈一体化系统的高效估计与补偿

由于气动参数摄动、外部扰动、目标机动等因素，IGC系统会存在大量匹配或非匹配的不确定性。当前多数方法都是基于反演/动态面法开展的，采用干扰观测等方法进行不确定性的估计与补偿。

此类方法为了建立严格反馈状态模型，在建模时往往强制忽略舵偏产生的加速度，将其作为干扰项处理，即将系统控制量产生的部分作用放入不确定性中近似处理，以系统鲁棒性抑制控制量自身引起的不确定。这种方法在调参时比较困难，稳定收敛域较小，尤其是对于特征点动态范围变化较大的对象和场景，严重制约了其适用范围。为此，需要探索针对非严格反馈、非匹配不确定对象的IGC设计方法，避免引入控制量相关的不确定性，以增大系统的稳定收敛域，提高系统的控制品质。

3)大落角约束下的多弹协同IGC设计问题

根据上述分析，IGC方法相对于传统的分离设计能更好地提升系统控制效果。近些年，多弹协同制导研究取得了长足进步，但多弹协同下的IGC设计相关研究还较少，尤其是具有落角约束的协同IGC方法。现有文献大都针对二维平面设计角度约束协同IGC方法，多属于隐式协同范畴，而且要求对系统的时间信息进行准确估计；此外，同时考虑视场角、输入等多约束情况的协同IGC方法更为少见，这是一个重要的研究方向。对于三维带角度约束的多弹协同情形，Wang等提出的IGC方法能够实现在理想集中通讯条件下的协同齐射攻击，并且不需要时间信息，但实际上属于部分IGC类型，并未充分利用各回路间的耦合关系。总之，考虑落角约束的三维多弹协同IGC目前属于比较新颖的研究方向，未来将具有很大发展潜力。

6 结束语

以对地/对海精确打击为背景，本文给出了终端角度约束的定义，建立了面向终端角度约束制导及制导控制一体化设计的状态空间模型，针对终端角度约束制导方法和制导控制一体化方法的研究现状进行了综述，并对其未来发展进行了展望。

对于终端角度约束的制导问题，当前研究方法众多，能够分别有效解决落角约束、视场状态约束、输入约束等问题。然而，相关假设前提使这些方法大多仍停留在理论层面，还需要在信息估计与制导协同设计、通道耦合/状态/输入/落角/速度等多约束制导、落角约束的可达范围估计与优化、大落角约束下的多弹协同制导等方面开展深入研究。

对于终端角度约束下的制导控制一体化设计问题，由于存在高阶性、强耦合性和非匹配不确定性，目前的主要研究思路是反演/动态面与滑模等各种方法的结合，在落角约束控制、视场状态约束、输入约束等方面取得了一定的进展。与大落角约束制导类似，三维场景下多约束共存的IGC设计以及大落角约束下的多弹协同IGC设计是目前亟待解决的关键技术。