非死锁合同网协议驱动的多机分布式时序任务分配
曹 严,龙 腾,孙景亮,徐广通
(1. 北京理工大学宇航学院,北京 100081;2. 飞行器动力学与控制教育部重点实验室,北京 100081;3. 清华大学精密仪器系,北京 100084)
0 引 言
多无人机(Unmanned aerial vehicle,UAV)协同能够扩展任务执行能力,提升任务完成效能。作为多无人机协同的关键技术之一,任务分配技术是在多任务、多目标及多无人机之间进行协调规划,考虑任务执行顺序、无人机性能等约束条件,以任务代价最小化为目标,将多任务合理分配给各机。耦合的任务时序约束对多机任务分配带来较大技术挑战,易造成多无人机因为时序冲突而陷入死锁现象,无法获得可行解。因此,有效避免时序任务分配中的死锁问题至关重要。
时序任务分配方法主要包括集中式与分布式两类方法。在集中式架构下,根据死锁产生机理,通过中心节点实现整个系统的非死锁任务调度。Edison等使用遗传算法求解时序任务分配问题,通过降低死锁个体的适应度实现系统非死锁分配。邓启波等基于图论建立任务时序优先级图,给出死锁一般形式,并定制转置操作对陷入死锁的个体进行解锁。文献[8-9]定制遗传算法的初始化和遗传操作,确保个体在进化过程中保持非死锁状态,提升了算法的全局最优性。Wang等提出改进量子粒子群算法,并设计时序任务次序调整策略,在算法迭代中有效生成非死锁任务序列,该方法较传统遗传算法提高了求解稳定性。然而,上述任务分配架构存在中心计算节点,依赖全局通信,因此系统抗毁性较差。另外,随着任务分配问题规模增大,集中式架构下任务分配方法求解耗时呈超线性增长,难以满足在线实时求解的需求。
分布式架构下各无人机不依赖于中心计算节点,通过机间通信协商实现任务的高效分配,系统具备更好的鲁棒性与稳定性。近年来,基于市场竞争机制的分布式任务分配算法受到广泛关注。吴薇楠根据任务间依赖性将时序耦合约束分为单边依赖、相互依赖与互斥约束。Jonese等在应对灾难响应问题中考虑消防车灭火与路障清理两类时序任务约束,采用分层拍卖算法对解空间进行快速有界搜索。文献[16-18]针对复杂任务环境,构建任务优先级图,将任务按时序关系分层,并定制迭代拍卖算法对各层任务进行高效求解。上述方法采用分层求解架构处理时序任务分配问题,有效规避了任务死锁现象,但固化了时序任务的分配次序,缩减了可行解空间,分配结果最优性有待进一步提升。Lim等在势博弈框架下引入一种调度算法处理复杂时序任务分配问题,显著提升了大规模问题的求解效率,但基于随机抽样的均衡选择方法使其结果最优性仍难以保证。陈璞等在通信约束任务分配问题中考虑了任务死锁约束,但该方法主要针对目标协同打击动态任务分配问题,未考虑多类型时序任务带来的复杂耦合影响。文献[21]提出了耦合约束一致性束算法(CBBA-TCC),在保留CBBA算法最优性特点的基础上,可短时内生成时序任务分配方案,但CBBA-TCC仅考虑两类时序任务,不适用于“察打评”多时序任务下无人机协同任务场景。因此,有必要充分考虑各时序任务的耦合关系与死锁影响,扩展可行解空间,在保证分布式架构下时序任务分配算法求解时效性优势的前提下,提升分配结果最优性。
本文针对分布式时序任务分配问题,提出了基于非死锁合同网协议(Deadlock-free contract net protocol, DF-CNP)的多机分布式任务分配方法,主要工作包括:
(1)提出了局部信息条件下时序任务死锁判据,实现各机根据局部信息判定全局任务死锁状态,有效解决分布式分配过程中的任务死锁问题。
(2)提出了最近邻-深度优先混合搜索算法(Nearest neighbor-depth first search,NN-DFS),利用最近邻准则降低任务排序代价,通过深度优先搜索满足任务非死锁约束,实现各机非死锁任务排序,提升分配结果最优性。
1 预备知识及问题建模
1.1 代数图论相关知识
通过构建有向图对无人机与时序任务间关系进行描述与分析。对于任意分配方案,可由有向图=(,)表示。中的元素称为的顶点,为的有向边集。若=(,)∈,则称为有向边的起点,为的终点。描述了任务间的时序关系,(,)表示应在前被执行。若存在一条从到的有向路,则称顶点到顶点是可达的。
1.2 时序任务分配建模
考虑个目标,多无人机需对每个目标依次执行侦察()、打击()、评估()任务,任务集表示为={,,…,},记任务数量为,则=3。考虑存在架异构无人机,表示为={,, …,},具体可分为战斗型、侦察型和打击型无人机。战斗型无人机可执行全部任务,侦察型无人机可执行侦察、评估任务,打击型无人机仅执行打击任务。本文假设各任务仅由单架无人机执行,且每个目标的任务时序为→→。
考虑任务执行过程中减小系统整体任务代价与均衡各机代价,以最小化无人机任务执行时长总和与整体任务完成时间为优化目标,构建多无人机时序任务分配模型如下
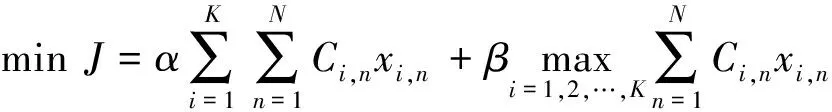
(1)
s.t.
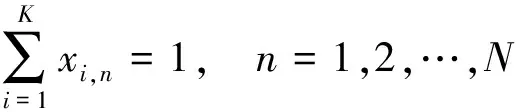
(2)
,∈{0,1}
(3)
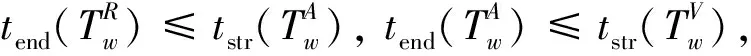
=1,2,…,
(4)
式中:,为权重系数,取值根据需求确定;,是二元变量,当任务分配给无人机时,, =1,否则为0;无人机完成任务的时长为
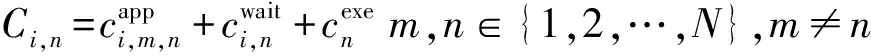
(5)
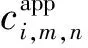
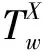
2 非死锁合同网协议算法流程
DF-CNP通过“招标-投标-中标”的规则实现任务的转移和分配。由于标书计算的独立性,该方法支持分布式并行求解,能够在局部信息条件下获得时序任务分配方案。局部信息条件具体为:在每轮协商中,招标者与投标者存在信息交互,而投标者之间无交互。
各机在分布式架构下并行运行DF-CNP实现多机非死锁时序任务分配,以无人机为例,DF-CNP算法流程如图1所示,具体步骤如下:
1)参数初始化。具体包括基本参数信息(初始位置、最小转弯半径)、招标者编号、目标位置、他机编号与类型。
2)生成非死锁初始分配方案。本文设计如下两条规则生成初始分配方案,规则I:各机按目标数量均匀分配,同一目标上的任务需统一分配至一架无人机。规则II:若按规则I生成的初始方案中某些任务超出能力范围(打击型无人机无法执行侦察任务),则将该任务按无人机编号转移至后续具备任务执行能力的无人机。
3)身份判断。每轮协商开始前,对自身身份进行判断,若当前身份是投标者,转入步骤7,等待招标者发布任务序列;反之,当前身份是招标者,执行步骤4)。
4)招标者发布任务序列。依次卖出持有任务,对剩余任务进行非死锁排序,并向市场内全体投标者发布剩余任务序列。
5)招标者发布中标信息。接收投标者发布的标书信息,从中选取标书值最大的无人机作为中标者,向市场公布中标结果。将卖出投标任务后的剩余任务序列作为更新后的任务排序方案。
6)判断是否满足招标者更新与算法收敛条件。若满足收敛条件,则向市场发布算法收敛信息,本机算法运行结束;若满足招标者更新条件,则招标者编号向后顺延。返回步骤3)。
7)若当前身份为投标者,接收招标者发布信息后,与其他投标者并行开展标书计算,将招标者卖出任务纳入自身任务序列,完成非死锁排序。依据排序结果与招标者剩余任务序列计算代价变化量,选择最小化整体代价的任务进行投标,并向投标者发布标书及对应投标任务。
8)投标者判断是否中标。若接收到中标信息则更新自身任务序列。若未中标,则保持原有任务序列。
9)若投标者收到算法收敛信息,则本机算法运行结束,按当前分配结果执行任务。若收到招标者更新信息,则招标者编号向后顺延。返回步骤3)。
DF-CNP算法步骤4)、6)、7)中涉及的非死锁任务排序方法、代价计算与标书生成、招标者更新策略与算法收敛条件是本文的主要创新点,详细描述见第3、4节。
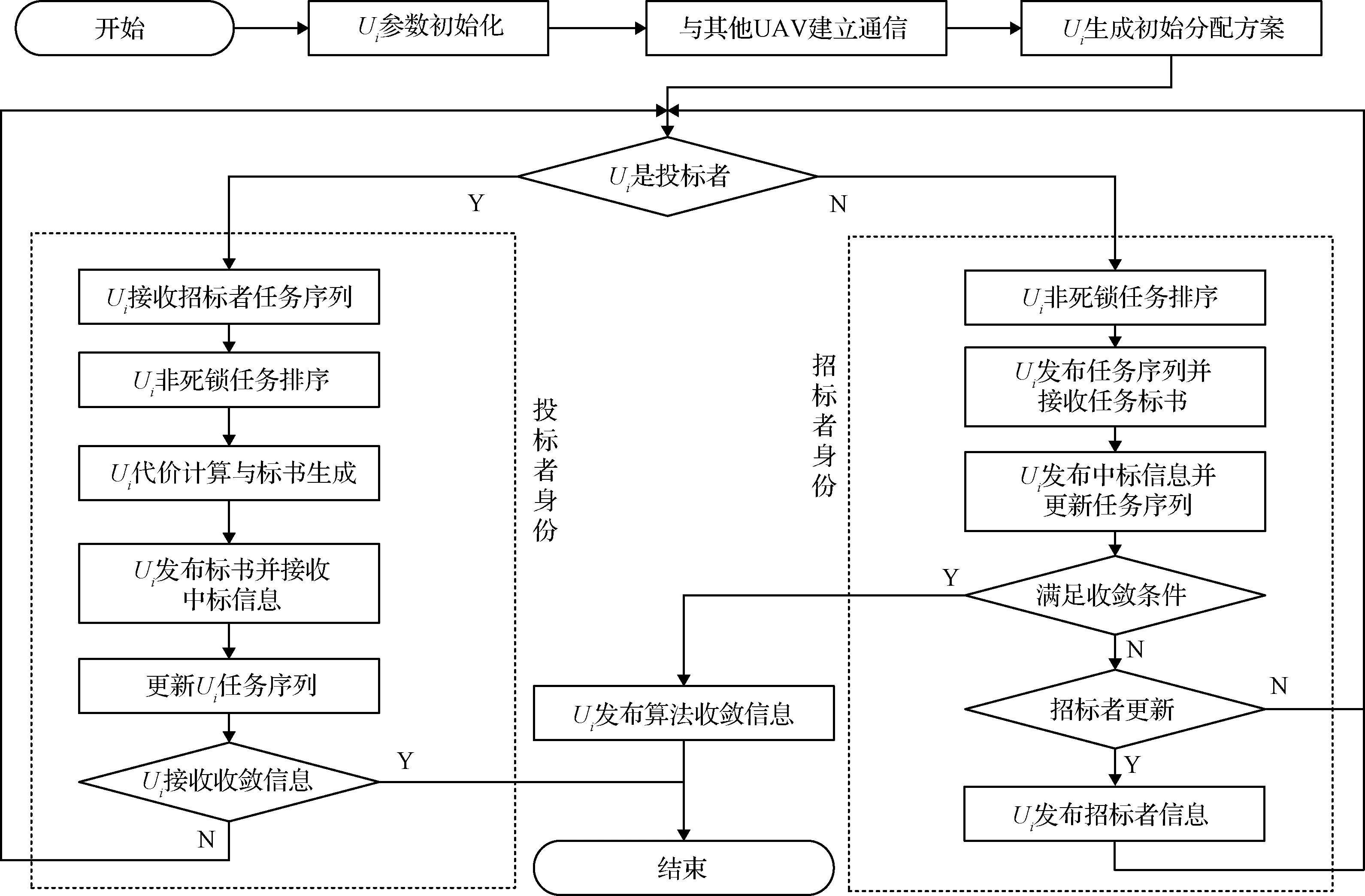
图1 DF-CNP算法流程图Fig.1 Flowchart of DF-CNP algorithm
3 局部信息条件下非死锁任务排序
针对时序任务分配中存在的死锁现象,本文给出了局部信息条件下的死锁判据,用于判断当前分配方案的全局任务死锁状态。提出了一种最近邻-深度优先混合搜索算法,对无人机自身任务进行非死锁排序,减小任务执行代价。
3.1 死锁判据
任务死锁是由不合理任务执行顺序导致的各机陷入无尽互相等待的现象,死锁分配方案对应有向图含环,环上每架无人机都在等待其他无人机任务执行结束。
全局任务分配方案对应有向图D,在局部信息条件下,本文考虑单机掌握的信息构成子图H, H⊆D,并给出如下定义。
指向子图H的有向边为子图H的入弧,其数量为子图I的入度,记为O。由子图H指出的有向边为子图H的出弧,其数量为子图H的出度,记为O。
H入弧的终点为H的入点,H出弧的起点为H的出点。若H中存在入点到出点是可达的,则该两节点称为H的边界可达对。
图2所示有向图D不存在环,因此图2为非死锁分配方案。虚线框内代表子图H,根据上述定义,,是H的入弧,,是H的入点,I=2;是H的出弧,是H的出点,O= 1;(,)是H的边界可达对。
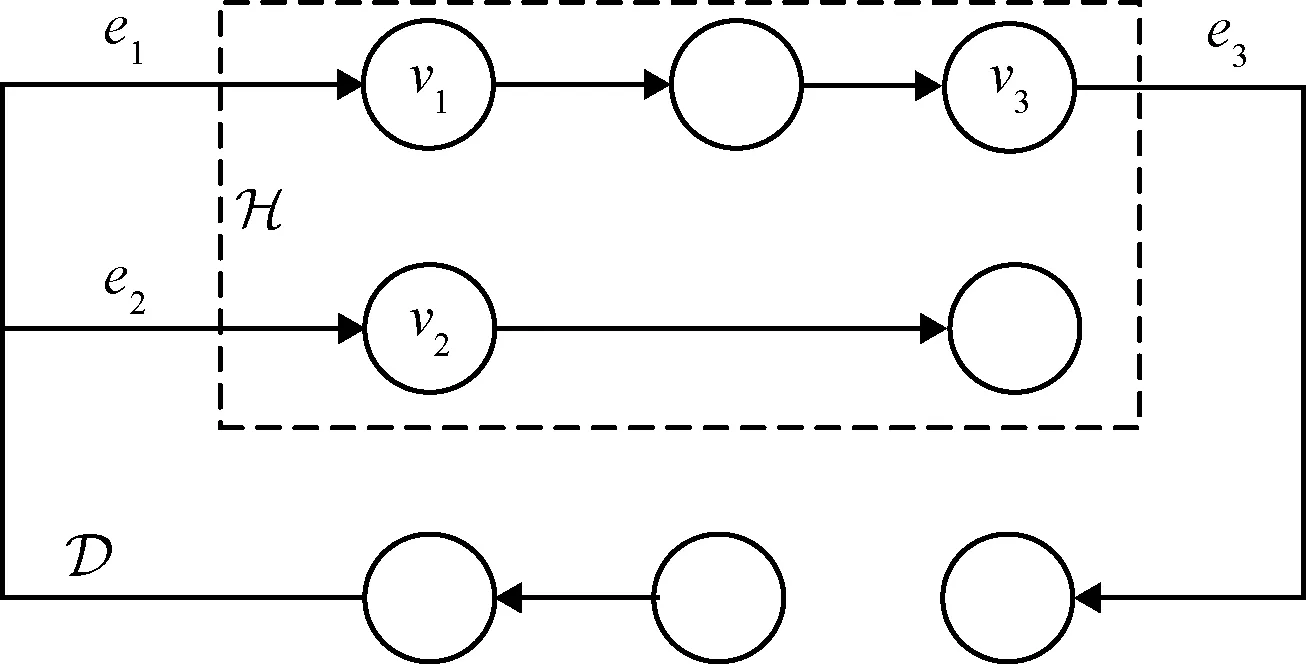
图2 典型有向图与子图示意图Fig.2 Typical directed graph and subgraph
在假设初始整体任务分配方案非死锁的前提下,本文提出单机根据局部信息(子图H)推断全局任务(有向图D)非死锁状态的判据,具体如下。
若I为0或O为0,只要任务调整后H无环,即可满足全局任务非死锁。
由于I为0或O为0,则H内任意节点无法与H外节点构成环路。由初始分配方案非死锁可知,H外节点构成的有向图内不含环路。因此,当H内节点局部调整后H无环,即整体有向图D均无环,从而保证全局任务分配方案非死锁,证毕。
若I和O均不为0,只要任务调整后H无环,且H不产生新的边界可达对,即可保证全局任务非死锁。
由初始分配方案非死锁可知,H外节点构成的有向图内不含环路。任务调整后H内无环,因此仅需考虑H内节点与外部节点构成环路的两种情况。
1) 任务调整前H存在边界可达对。任务调整后,若该边界可达对仍存在,考虑到局部任务调整对外部节点状态无影响,且调整前外部节点与该边界可达对不构成环路,因此调整后其与外部节点仍不构成环路;若任务调整后该可达对不存在,则其与外部节点不构成环路。由于该可达对的任意性,调整后的边界可达对状态均无法导致D产生环。由于任务调整不产生新的可达对,因此保证全局任务在调整后非死锁。
2) 任务调整前H不存在边界可达对,由调整后H不产生新的边界可达对可知,调整后H内任意节点与H外节点无法构成环路,因此整体有向图D均无环。满足全局任务非死锁,证毕。
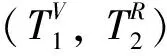
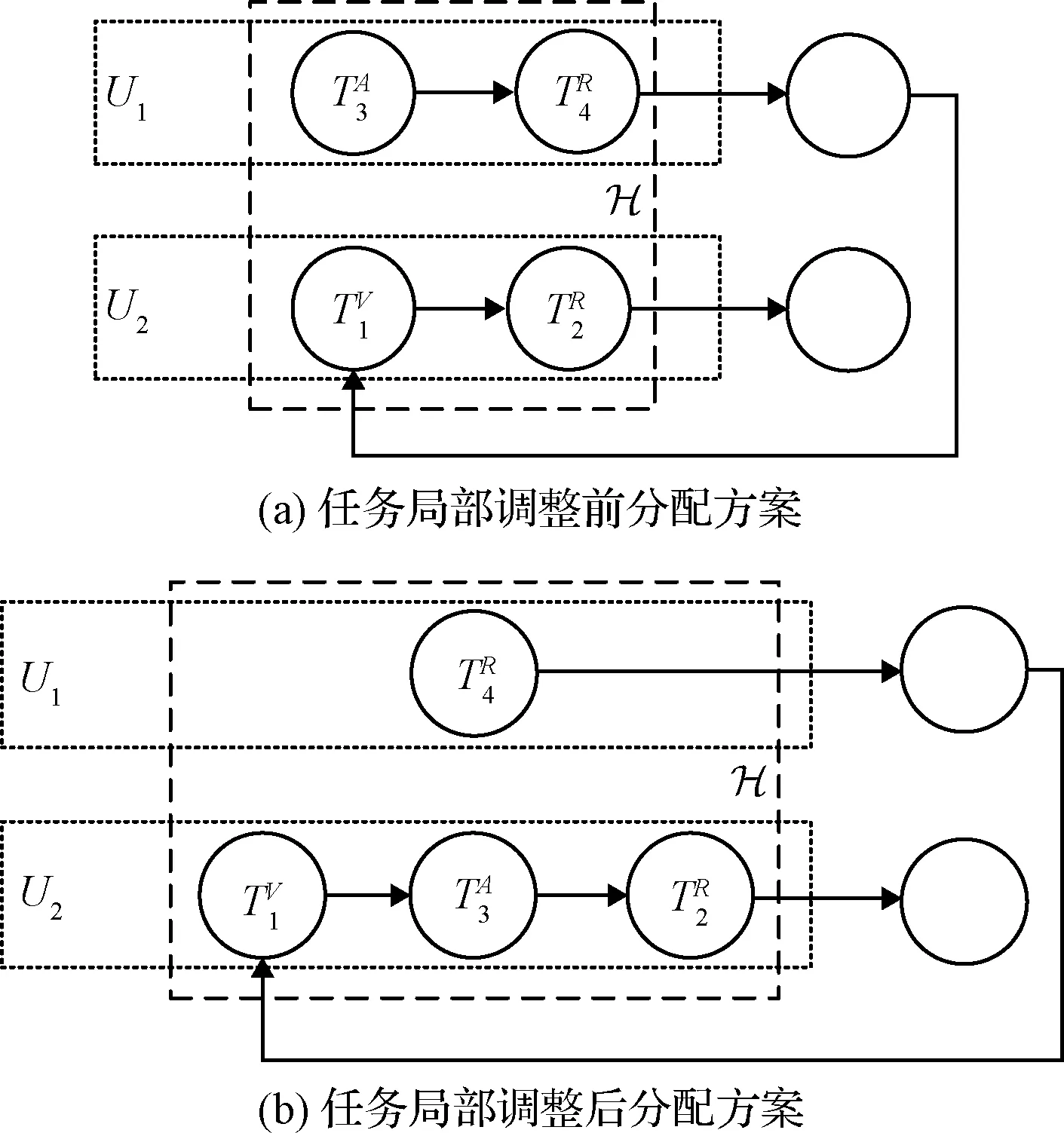
图3 任务死锁判断示例Fig.3 Example of task deadlock judgment
结合判据1~2,单机根据局部信息推断全局任务满足非死锁状态的判据可由式(6)表示
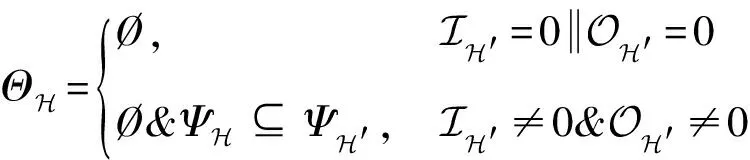
(6)
式中:H′表示调整前的子图;表示子图H内环路集合;表示H内边界可达对集合。
依据上述判据,无人机在分布式协商过程中仅需依据局部信息构建整体任务有向图子图,通过检测环路状态和子图边界可达对状态,即可推断分配后全局任务的死锁状态,舍弃陷入死锁的交易结果,保留非死锁方案持续分配过程。
3.2 非死锁任务排序
本文提出一种最近邻-深度优先混合搜索算法对各机任务排序。最近邻搜索是在排序中,选取距离当前任务最近的下一任务排入任务序列,从而降低任务执行代价,但排序过程无法考虑任务间时序关系。为此,通过深度优先搜索递归回溯实现对可行解空间的持续探索,运用死锁判据消除陷入死锁任务排序方案,确保全局任务分配结果的可行性。
设当前任务集为,为无人机持有的任务数量。考虑中任务与,构建任务间预估代价矩阵={}×,其中:
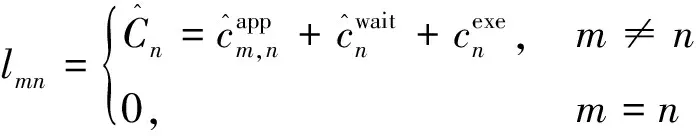
(7)
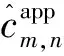
NN-DFS基于进行非死锁任务排序,具体算法步骤如下:
1)参数初始化。将持有任务视作多个节点,当前节点=1,标记全部节点状态为未访问节点,初始搜索深度=0,初始搜索次数=0。
2)任务排序。依据预估代价矩阵选择的最近邻节点*加入任务序列,标记*为已访问节点,=+1,并更新*为当前节点进行最近邻排序。重复该步骤,直至=,表明NN-DFS当前已得到一组完整的任务序列,此时令=+1。
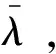
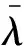
4 代价计算、招标者更新与收敛条件
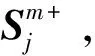
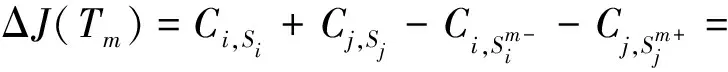
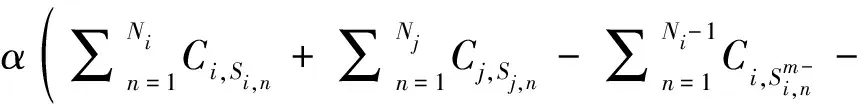
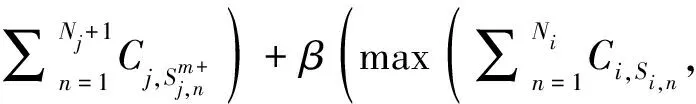
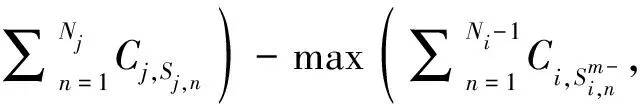
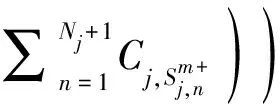
(8)
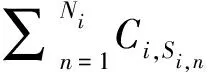
依次对中的所有任务计算买卖前后的代价变化,从中选取最小化整体代价的任务作为投标任务*,并发布标书值B,为代价变化的最大值。
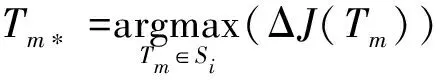
(9)
B,=Δ(*)
(10)
招标者汇集标书后,根据DF-CNP步骤5决策本轮中标者。通常,招标者的选取通过对比各机任务负载(任务数量、预期航程)选举产生。但任务负载小的无人机较难成为招标者,因此部分解的搜索空间被限制。为提升任务分配方案的最优性,设计招标者更新条件为:当多轮协商买卖后的系统整体代价无法降低,且仍存在无人机未担任招标者。
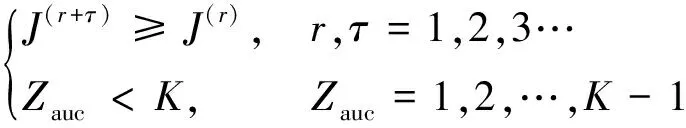
(11)
式中:表示第轮交易;为收敛指定迭代次数;为招标者编号;为无人机数量。此时招标者身份按编号顺移至后续无人机。
算法收敛条件为:若多次买卖后系统整体代价无法降低,且全部无人机均已担任过招标者,则算法收敛退出,此时式(11)中=。通常的选取与时序任务数量相关,文中需执行侦察、打击和评估任务,则取≥3。
5 仿真校验
本节在典型的任务场景下,通过仿真试验验证DF-CNP的有效性,并与非死锁遗传算法(TB-GA)、CBBA-TCC算法进行性能对比。其中对CBBA-TCC算法进行适应性改进,使其能够处理包含3类时序任务的问题。DF-CNP基于分布式架构,因此仿真试验在多台PC机上进行,计算耗时统计中考虑硬件通信传输延迟带来的影响,模拟多架无人机在真实环境下分布式信息交互。仿真硬件环境为Inter Xeon E5-4620 2.2 GHz处理器和16 G内存;软件环境为Visual Studio 2015。
为充分体现本文方法的最优性,根据文献[9]仿真参数设置,将TB-GA交叉概率与任务时序变异概率分别增加至0.85与0.3,种群规模与最大迭代次数分别增加至200与100,提升对比算法最优性;CBBA-TCC中无人机任务容量设置为想定中总任务数量,其余参数设置参考文献[21],其中任务价值递减系数根据文献[21]中救援任务设置为0.1。
5.1 想定I
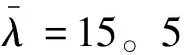
任务分配结果如图4所示,其甘特如图5所示。甘特图中方块左端时刻代表无人机开始执行当前任务,方块右端时刻代表无人机完成当前任务。方块之间的时间间隔代表无人机抵近或等待执行任务时长。由图4和图5可知,上述时序任务分配结果满足异构飞行平台约束和任务时序非死锁约束。
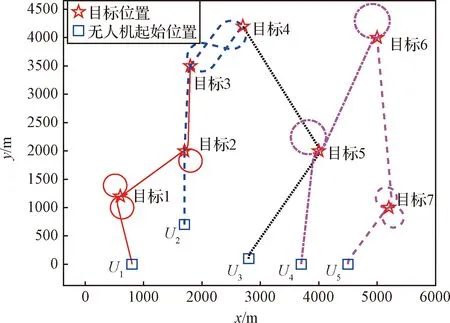
图4 任务分配结果(想定I)Fig.4 Task allocation result for Scenario I
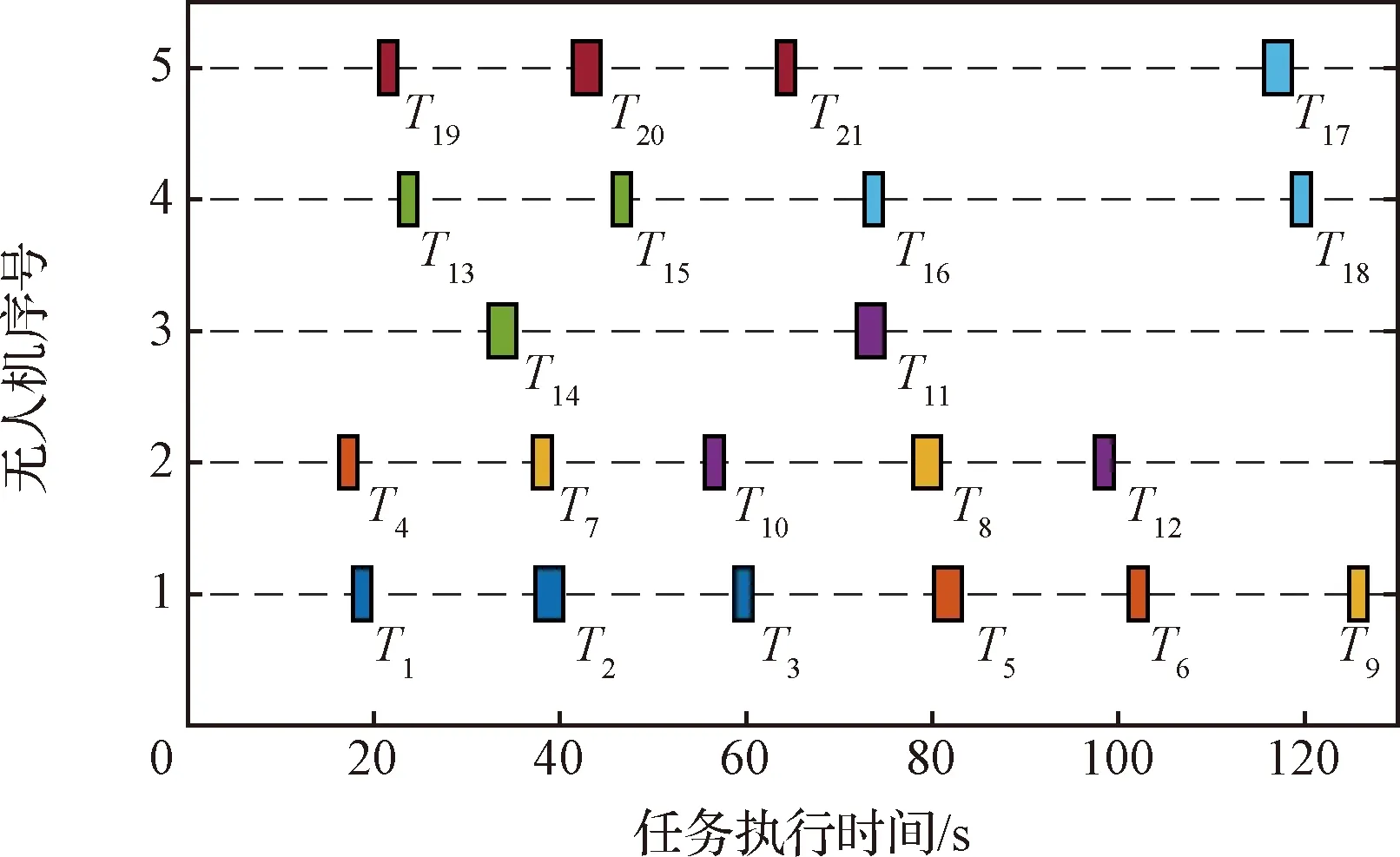
图5 任务执行时间甘特图(想定I)Fig.5 Gantt chart of task execution time for Scenario I
为充分对比DF-CNP、TB-GA、CBBA-TCC的最优性与时效性,开展50次仿真测试,统计结果如图6所示。DF-CNP目标函数均值(126.8 s)与计算耗时均值(0.489 s)相比TB-GA(目标函数均值138.6 s、计算耗时均值23.32 s)分别降低了8.5%与97.9%,表明DF-CNP在确保求解最优性的前提下,计算效率具有明显优势。由图6中数据散布可知,TB-GA计算结果具有一定随机性,而DF-CNP为确定性算法,其求解鲁棒性更优。与CBBA-TCC(目标函数均值152.8 s、计算耗时均值0.274 s)相比,DF-CNP在满足亚秒级规划效率的前提下,最大任务执行时长降低了20.5%,表明DF-CNP求解结果的最优性更高。
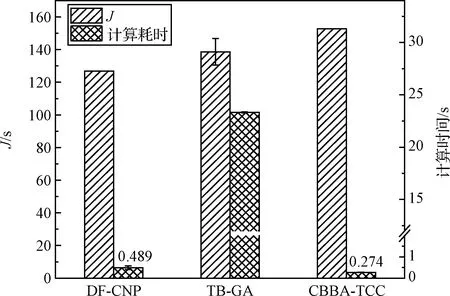
图6 算法最优性与求解耗时对比(想定I)Fig.6 Comparison of optimality and runtime for Scenario I
5.2 想定II
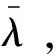
图7 任务执行时间甘特图(11个目标规模)Fig.7 Gantt chart of task execution time involving 11 targets
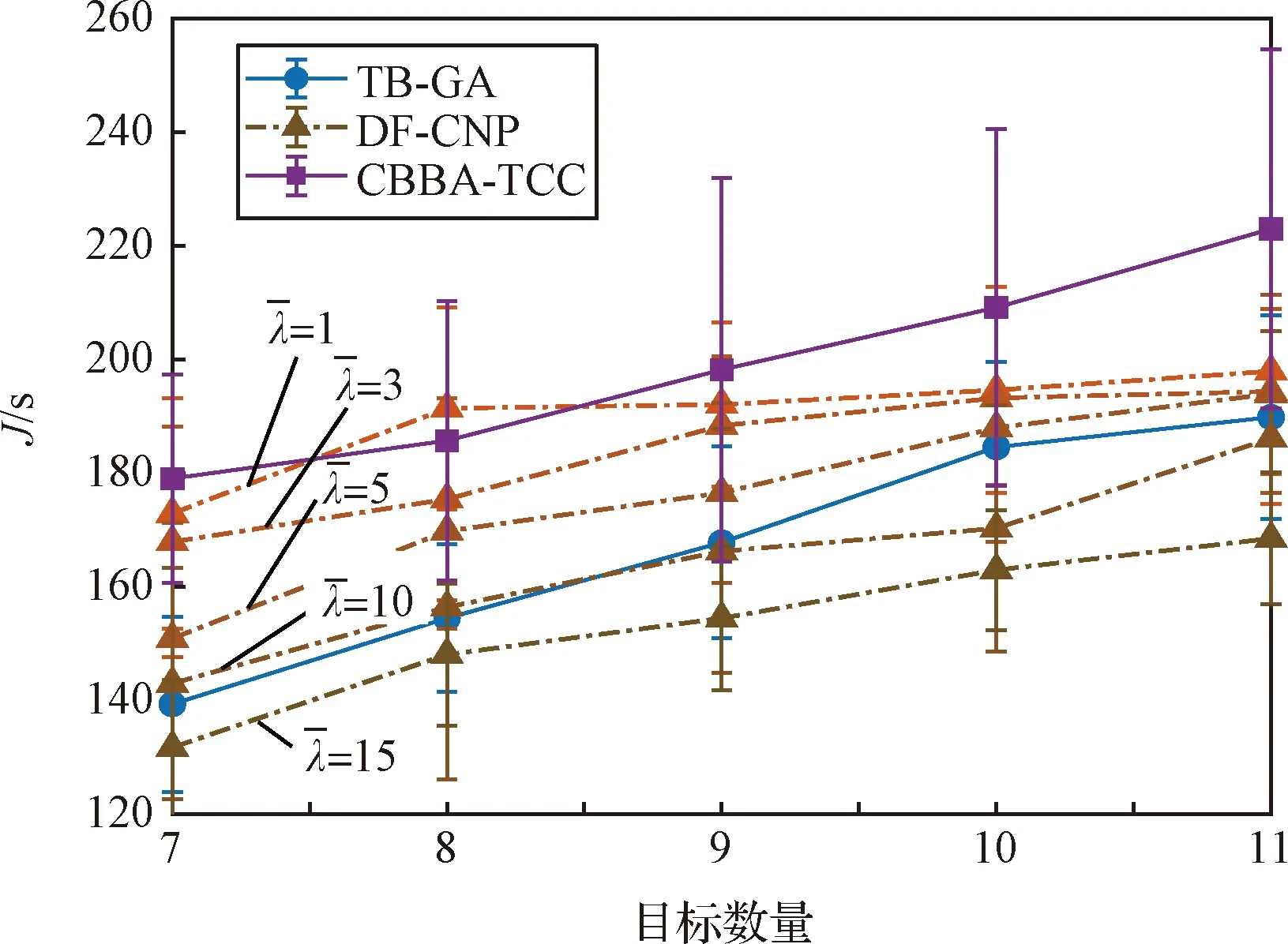
图8 代价值对比结果(目标规模7至11个)Fig.8 Comparison of cost involving 7 to 11 targets
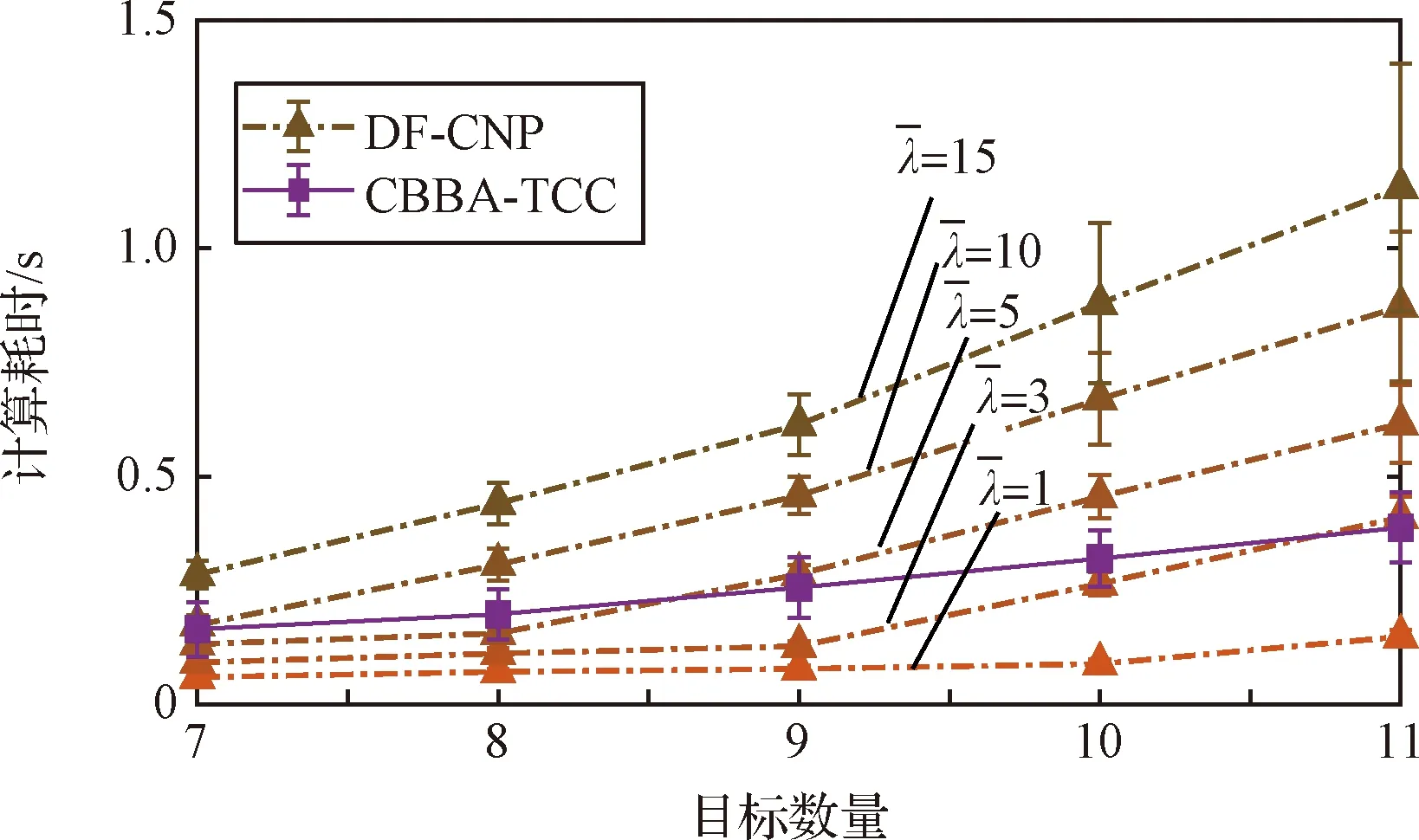
图9 求解耗时对比结果(目标规模7至11个)Fig.9 Comparison of runtime involving 7 to 11 targets
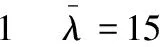
表时算法求解代价值标准差Table 1 Standard deviation of solution cost under
综上可得,DF-CNP能够实现异构无人机时序任务分配的非死锁约束。通过非死锁任务排序与招标者更新策略定制,充分扩展了合同网算法对最优解的搜索空间,提高了结果最优性;在分布式架构与市场竞争机制下,DF-CNP处理较大规模问题具备在线求解能力。
6 结 论
为实现分布式架构下异构无人机非死锁时序任务分配,本文基于市场竞争机制提出了非死锁合同网协议,通过仿真试验验证了研究成果的有效性,具体结论如下:
1)在初始全局任务分配方案满足非死锁约束的前提下,本文提出了局部信息条件下任务死锁判据,并定制了最近邻-深度优先混合搜索算法,实现各机非死锁任务排序,提升分配结果最优性。
2)本文提出的DF-CNP支持在分布式架构下有效处理异构无人机时序任务分配问题。通过与TB-GA及CBBA-TCC等算法对比,DF-CNP具备更好的求解最优性,并满足在线规划时效性需求。随着想定中无人机和目标的规模增加,DF-CNP求解最优性优势更为明显。
DF-CNP采用了传统的买卖合同机制,对有效解空间的搜索能力有限,后续研究中可定制多类型合同机制,进一步提高算法最优性。

