拦截大气层内机动目标的深度强化学习制导律

邱潇颀，高长生，荆武兴

(哈尔滨工业大学航天工程系，哈尔滨 150001)

0 引 言

近几十年，在拦截弹制导律设计领域，比例导引(Proportional navigation，PN)因其结构简单、易于实现的特点得到了广泛应用。对于无机动或弱机动性的目标，PN具备较好的拦截性能。但是，近年来飞速发展的导弹突防技术大大提升了进攻导弹的机动性，使得PN在面对此类高速、高机动性目标时显得力不从心，拦截效率显著下降。为了应对目标的强机动性，增强比例导引(Augmented proportional navigation，APN)应运而生。APN通过将目标的加速度信息叠加到PN制导指令上，实现对目标机动的补偿。然而APN需要实时获取目标的加速度信息，这给实际应用增加了难度。

当前，各类改进型的PN、最优控制和非线性控制等技术被广泛用于先进制导律的设计中。Lee等基于对剩余时间的精确估计，在PN中引出角度误差反馈项，设计了一种拦截角控制导引律，使导弹能以特定角度命中目标；Jeon等着眼于多枚导弹对单一目标的协同打击问题，通过在PN中加入命中时间误差反馈项，提出了撞击时间控制导引律。文献[6]基于最优控制理论和双曲正切函数，设计了考虑角度约束的最优三维制导律，有效解决了传统导引律初始段过载指令过大的问题。Li等针对大初始航向误差的情况，基于非线性模型设计了包含角度约束的机动目标最优拦截制导律，避免了线性最优导引律在面对较大初始航向误差时制导指令易发散的弊端。文献[8]提出了一种在特定时间拦截非机动目标的非线性次优三维制导律，同时避免了在制导律中引入剩余时间项。张浩等基于线性二次型微分对策理论，设计了面向具备主动防御能力目标的拦截制导律，促使拦截弹在规避敌方防御弹的同时能够有效杀伤目标。在基于非线性控制理论的制导律设计中，滑模和自适应方法应用最为广泛。结合非奇异快速终端滑模控制与自适应算法，黄景帅等提出了一种无需目标加速度信息的自适应制导律，能够保证误差的有限时间收敛性。文献[12]利用神经网络来搭建目标加速度预测模型，并在此基础上设计了拦截高超声速目标的最优滑模制导律，在节省燃料的同时减小了拦截末端的指令加速度。同样利用神经网络技术，司玉洁等针对执行器饱和问题，设计了一种自适应滑模制导律，一定程度上提升了制导律的鲁棒性。然而，上述导引律中的大多数是基于精确动力学模型推导所得，且需要剩余飞行时间或目标加速度等信息，这势必会增加其应用难度。

强化学习(Reinforcement learning，RL)为拦截弹制导律的设计提供了一种新思路。其作为人工智能领域的一个重要分支，近些年发展迅速。RL通常可由马尔可夫决策过程(Markov decision process，MDP)来描述，包含智能体和环境两部分。智能体不需要任何监督信号或精确的环境模型，而是通过与环境进行交互来改善自身策略，因此RL被认为是区别于监督学习和无监督学习的第三种机器学习范式。随着深度学习(DL)技术的成熟，结合DL和RL的深度强化学习(DRL)算法开始逐渐涌现，例如深度确定性策略梯度(Deep deterministic policy gradient，DDPG)、双延迟深度确定性策略梯度(Twin delayed deep deterministic policy gradient，TD3)以及近端策略优化(Proximal policy optimization，PPO)等。当前，DRL技术被广泛应用于行星探测、多弹/机协同制导、巡飞弹突防制导等领域，展现了良好的性能和广泛的应用前景。而在拦截弹制导律设计方面，国内外众多学者先后开展相关研究，但仍处于起步阶段。考虑到红外导引头仅能获取目标角度信息的限制，Gaudet等结合PPO算法和元学习技术，设计了面向大气层外机动目标的离散动作空间拦截导引律，然而这种离散动作并不适合于大气层内拦截。He等探索了将DDPG算法应用于拦截弹制导律设计的可能性，通过对比从零学习和基于先验知识的两种学习模式，指出后者有助于提升学习效率，并可能提供更好的拦截性能。然而DDPG算法所固有的收敛速度较慢、学习稳定性差等缺陷难以避免。

本文针对DDPG算法的上述固有缺陷，通过引入双重Q网络和延迟更新来改善算法学习效率，进而提出了一种基于TD3算法的拦截大气层内高速机动目标的深度强化学习制导律。首先将攻防双方交战运动学模型描述为适用于深度强化学习算法的马尔可夫决策形式,引入奖励整形函数来进一步提升算法学习速度，并通过在训练过程中随机初始化攻防双方的状态来提升算法所学到最终制导律的泛化能力。仿真结果验证了本文制导律的可行性，与PN、APN等传统导引律相比，它不仅能够降低对拦截弹中制导精度的要求，而且脱靶量更小。在多种不同工况下的蒙特卡洛仿真结果表明，该制导律具备良好的鲁棒性和泛化性。

1 问题描述

本节给出典型拦截场景下交战双方的运动模型，并将其描述为适合于深度强化学习算法的马尔可夫决策过程。在此之前，我们做出如下三点假设：

拦截弹和进攻弹双方均被视为质点运动模型；

忽略拦截弹导引头及其控制系统的动态特性，视为理想制导过程；

拦截弹和进攻弹的飞行速度均视作常值。

以上三点假设在导弹制导律设计中被广泛采纳。假设1和假设2代表了一种将制导回路和控制回路分开处理的思想：其中制导系统作为外回路，来生成由内部控制回路负责跟踪的制导指令。假设3则是考虑到拦截高速机动目标的末制导阶段持续时间较短，速度变化并不显著，因此将其视为常值。

1.1 交战场景

本文研究了如图1所示的纵向平面内交战场景。图中M表示进攻方导弹，D代表防御方拦截弹，而T为进攻方所要打击的固定目标。显然在此场景下，进攻弹M需要在躲避拦截弹D的同时命中目标T；而拦截弹D的任务就是要尽可能地拦截M从而保护T免遭杀伤。

图1 交战场景Fig.1 Engagement scenario

在图1中，笛卡尔惯性坐标系-T-代表交战所发生的纵向平面，其中目标T位于坐标原点。,,分别表示目标-进攻弹，目标-拦截弹和拦截弹-进攻弹之间的距离；,,则代表相应的视线角。和分别为拦截弹和进攻弹的弹道倾角，以正向为基准，逆时针转动为正。拦截弹和进攻弹的飞行速度在图中分别由与表示；而它们的法向加速度则被分别表示为和。

忽略重力的影响，上述场景下目标-进攻弹之间的交战运动学为：

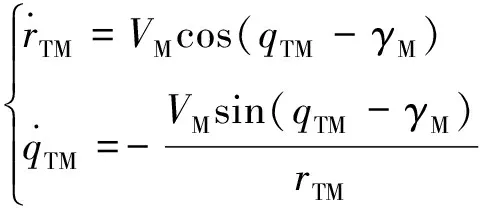
(1)

同样可以得到目标-拦截弹之间的交战运动学为：

(2)

而攻防双方的弹道倾角可分别表示为：

(3)

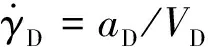
(4)

需要说明的是，这里并未直接采用拦截弹-进攻弹之间的相对运动模型的原因是便于执行如图4所示的状态随机初始化，以提升深度强化学习算法所学到最终策略的泛化能力。此外，在算法训练中为进攻弹M设计如下机动策略，以契合其躲避拦截弹D并打击目标T的战术目的：

=

(5)

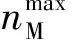
式(5)所示进攻弹M的机动模式意味着：当拦截弹D迫近到≤时，M会执行一个持续时间为、频率为的方波机动，以躲避D的追击；而在其他时间，M则是依据与目标T的相对运动关系，按照比例导引律来打击目标。显然这种机动模式与M的战术目的相一致。

1.2 马尔可夫决策过程

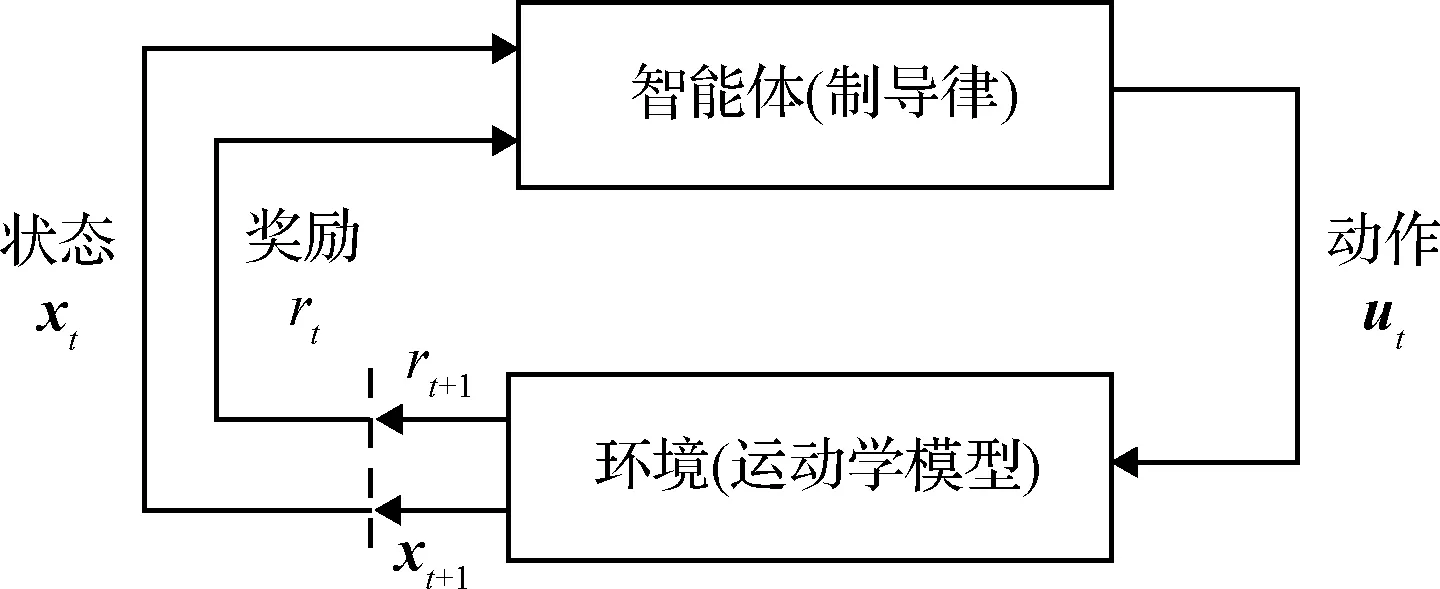
图2 MDP中智能体与环境交互过程Fig.2 Agent-environment interaction in MDP

在某一训练回合中，智能体模块在每一时刻观测到此时的交战状态，并依据当前策略(|)来决定所采取的动作～(|)。其中(|)定义为：

(6)

之后环境中的交战运动学方程在此动作的作用下向前积分一步，得到下一时刻状态+1的同时，智能体模块将获得一个来自环境的奖励+1。循环执行此交互过程直至该回合结束。在一个回合中，从时间到终止时刻,智能体所获得的总奖励可定义为：

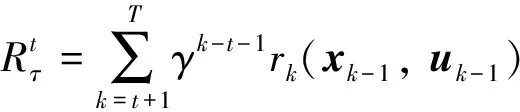
(7)

式中：={,,+1,+1, …,,}表示某一回合所对应的状态-动作轨迹；∈[0, 1]为折扣因子。

2 基于深度强化学习的制导律设计

2.1 深度强化学习

()=Ε[|=]

(8)

(,)=Ε[|=,=]

(9)

从而可将强化学习算法所优化的目标函数定义为：

≐()=Ε[|=]

(10)

此时，强化学习便可以通过最大化如式(10)所示的性能指标来获取最优策略(|)。为此，可以采用一个参数化的策略函数(|;)来近似最优策略(|)，进而通过调整参数来提升性能指标的值，从而实现对策略(|;)的优化。这可以通过式(11)所示的梯度上升法来实现，

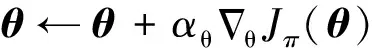
(11)

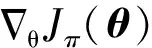
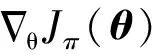
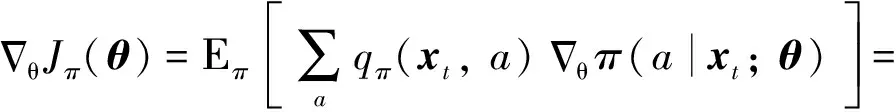
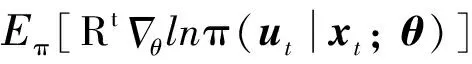
(12)

为了进一步降低算法训练过程中的方差，可以引入一个基线函数()，从而可以将式(12)改写为：

(13)

更进一步，利用动作价值函数(,)的参数化近似(,;)和状态价值函数()的参数化近似(;)，来分别替代式(13)中的和()两项，便可以得到执行者-评价者(Actor-Critic)算法的梯度更新方向为：

(14)

式中：(,;)=(,;)-(;)称作优势函数。

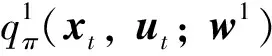
在引入经验回放机制后，用于更新价值函数网络参数的损失函数可以定义为：

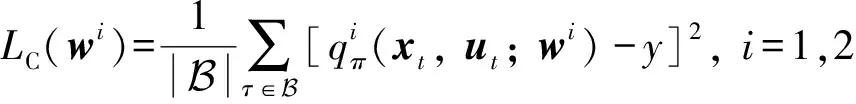
(15)

式中：|B|代表数据集B的长度。

与深度Q学习不同的地方在于上式中的表达式，TD3算法在计算时选用了两个价值函数目标网络中输出较小的那一个，以避免对价值函数的过估计；并且在策略目标网络输出的动作～(|;)的基础上叠加了一个随机噪声，以提升算法稳定性。因此式(15)中的表达式为：

(16)

式中：～((0,),-,)，其中函数定义为：

相应地，策略网络(|;)参数更新的损失函数可表示为：

(17)

参数和便可分别按照式(18)、(19)更新，以最小化损失函数()与()。

(18)

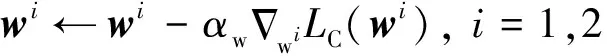
(19)

为了保证训练的稳定性，TD3算法中三个目标网络的参数可按下式进行软更新：

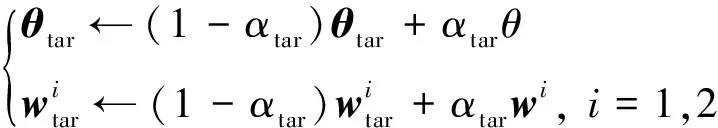
(20)

式中：被称为惯性因子。

需要补充的是，为了保证算法在训练中具有足够的探索性以避免陷入局部最优点，与DDPG算法类似，需要在动作～(|;)的基础上叠加一个随机噪声N～((0,),-,)。

2.2 制导律设计

基于上文所介绍的TD3算法和式(1)～(4)所示的攻防双方交战运动学方程，图3展示了本文所设计的深度强化学习制导律全系统结构框架。如图所示，系统环境是在交战运动学模型的基础上，又附加了状态随机初始化和随机航向误差而搭建起来的。在训练中引入随机初始化和随机航向误差均是为了提升算法所学习到最终策略的鲁棒性和泛化能力。

图3 系统结构框图Fig.3 Block diagram of the system

1)训练场景

为了保证TD3算法的训练速度，需要对攻防双方的初始状态做出如图4所示的限制。其中为初始视线角TM与TD的下界，而则为上界；和分别为初始目标-拦截弹距离的上界与下界，而和则是初始目标-进攻弹距离TM的边界。此外，将拦截弹的初始航向误差表示为，即拦截弹的初始航向角为：

(21)

式(21)意味着当=0时，拦截弹的航向满足进攻弹不机动时的碰撞三角。

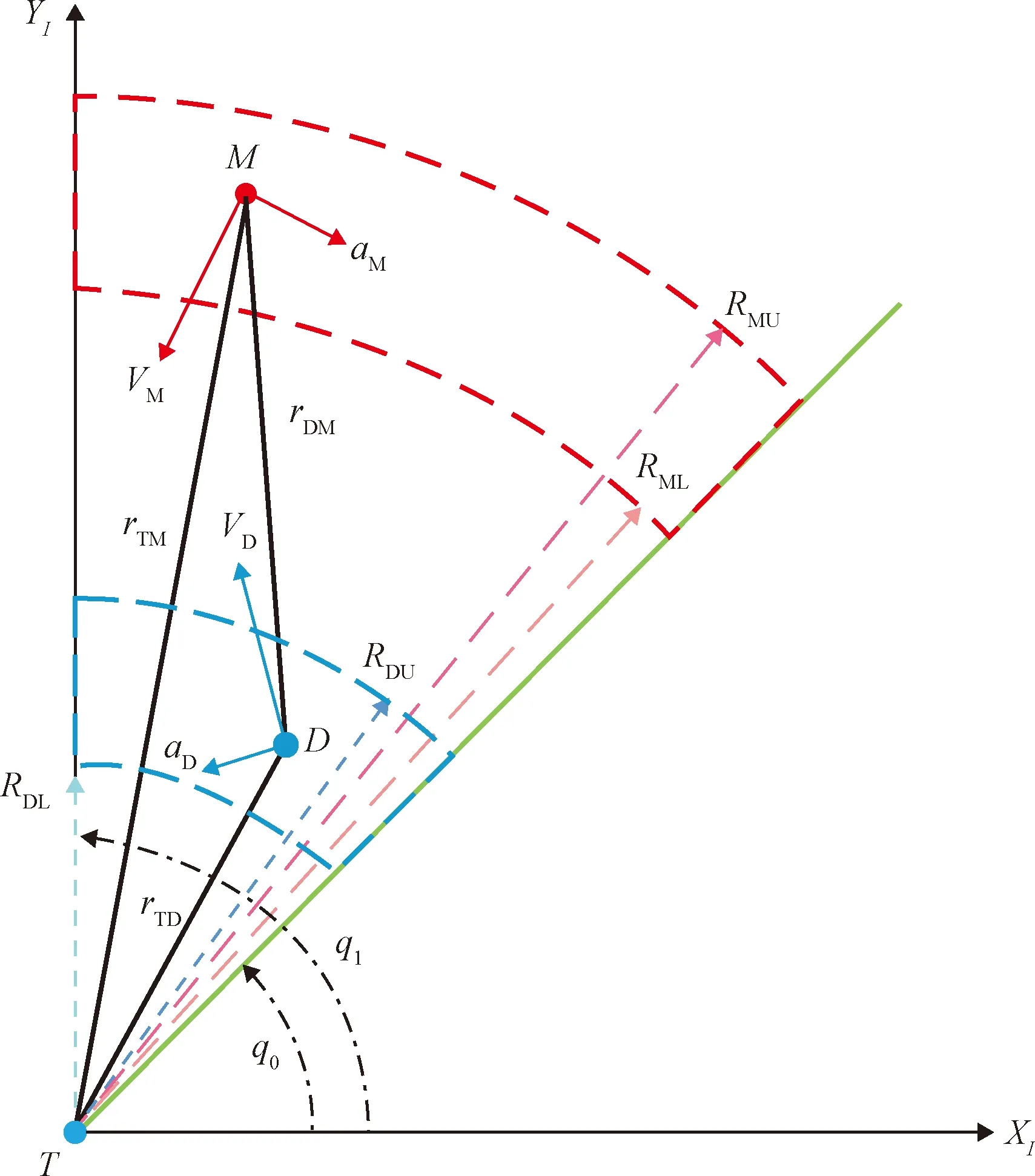
图4 训练场景Fig.4 Training scenario

表1 训练场景边界Table 1 Limits of the training scenario

2)状态空间与动作空间

在深度强化学习算法中，策略网络(|;)直接将状态量映射为动作，也就是说策略网络本身相当于一个如式(22)所示的非线性函数

=()

(22)

对于本文所研究的交战场景，拦截弹的战术目的就是尽最大可能拦截进攻弹，因此可将状态空间设计为拦截弹-进攻弹之间的相对状态，即：

(23)

而当假设速度为常值时，拦截弹的运动状态便仅由其法向加速度控制，因此可将动作空间设计为：

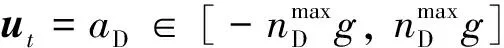
(24)

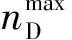
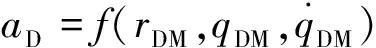
(25)

3)奖励函数

设计一个合适的奖励函数对于强化学习算法来说至关重要，会直接影响到算法的训练速度甚至是可行性。为了解决稀疏奖励所造成的算法收敛性差、学习速度慢等问题，本文引入了奖励函数整形。所设计的奖励函数为：

=+

(26)

其中：

=exp(-(Δ))+

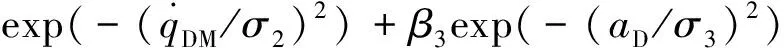
式中：和均为超参数; Δ=-DM。

4)网络结构

策略网络和价值函数网络均由包含三个隐含层的全连接神经网络来实现，其中隐含层的激活函数选取为ReLU函数，其定义为：

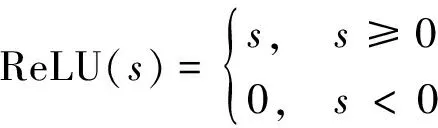
(27)

表2 网络结构Table 2 Architecture of the networks

3 仿真校验

为验证所提出基于TD3算法的拦截弹制导策略的有效性，本节开展了数值仿真。首先通过合理地选取超参数，得到了训练过程曲线。之后在多种不同工况下对所提出制导方案展开测试，并基于蒙特卡洛仿真与比例导引(PN)和增强比例导引(APN)两种经典制导方案作对比，体现本文方案的性能。

3.1 训练过程

本文中所有的仿真实验均是基于Python 3.7和Tensorflow 2.4框架开展的。硬件信息为Intel i7-10700K@3.80 GHz,RTX2070 8 GB,DDR4 16 GB,512 GB SSD。

强化学习训练环境由四阶龙格库塔积分器进行更新，当拦截弹-进攻弹的距离大于500 m时，积分步长为0.01 s；反之，积分步长取为0.0001 s。拦截弹和进攻弹的制导周期均取为0.05 s；总的训练回合数取为=50000。附加在动作值上的随机噪声N的界限在前5000个回合内由0.05逐渐衰减为0；而只有当经验池中的经验数量大于50000时，才会开始更新网络参数。训练中相关超参数的具体数值如表3所示。

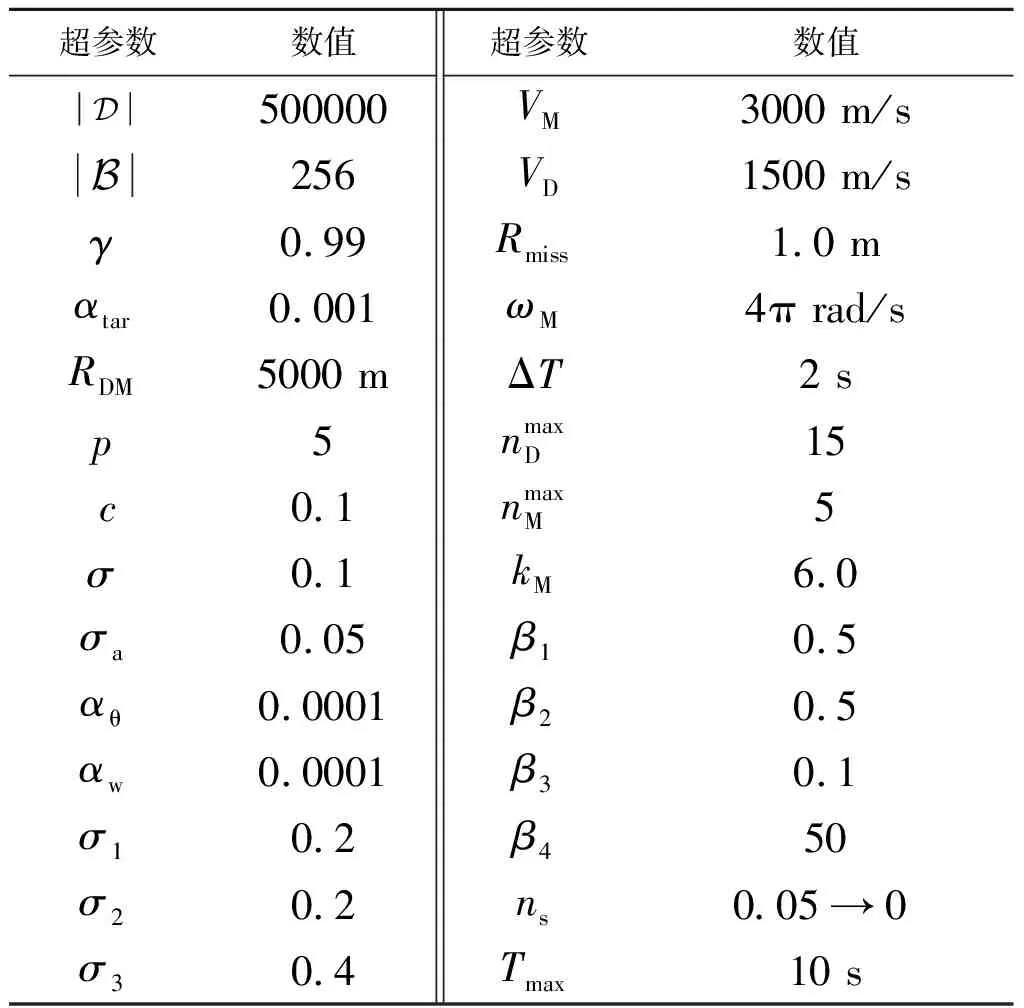
表3 训练所需超参数Table 3 Hyper-parameters needed in training

在训练过程中，为了保证算法所得到最终策略的泛化能力，拦截弹和进攻弹的初始状态分别在图4所示的可行域内随机初始化，且拦截弹的初始航向偏差也按照表1给出的范围随机选取。图5展示了算法的训练过程，其中图5(a)给出了训练过程中智能体每次与环境交互所得平均奖励的变化曲线；图5(b)则给出了经过不同回合数的训练后，所得到的策略在1000次蒙特卡洛仿真测试下的性能表现。综合图5可见：在算法训练的最初15000个回合内，智能体处在探索阶段，所获得的奖励值徘徊在低位，此时所得策略的拦截成功率几乎为0，性能很差；而在训练进行到第15000～35000回合中间时，智能体所获得的奖励开始逐渐增加，同时策略的拦截成功率也逐步提升、脱靶概率显著下降，这说明在此阶段策略得以优化；而在训练进行到35000回合以后，奖励值平稳地维持在高位，同时所得策略的拦截成功率也始终保持在较高水平，这说明此时算法逐渐收敛。此外由图5(a)中的算法对比曲线可见，本文所采用的TD3算法相对DDPG在学习速度上有明显提升，能够更早地改善智能体策略并达到收敛。

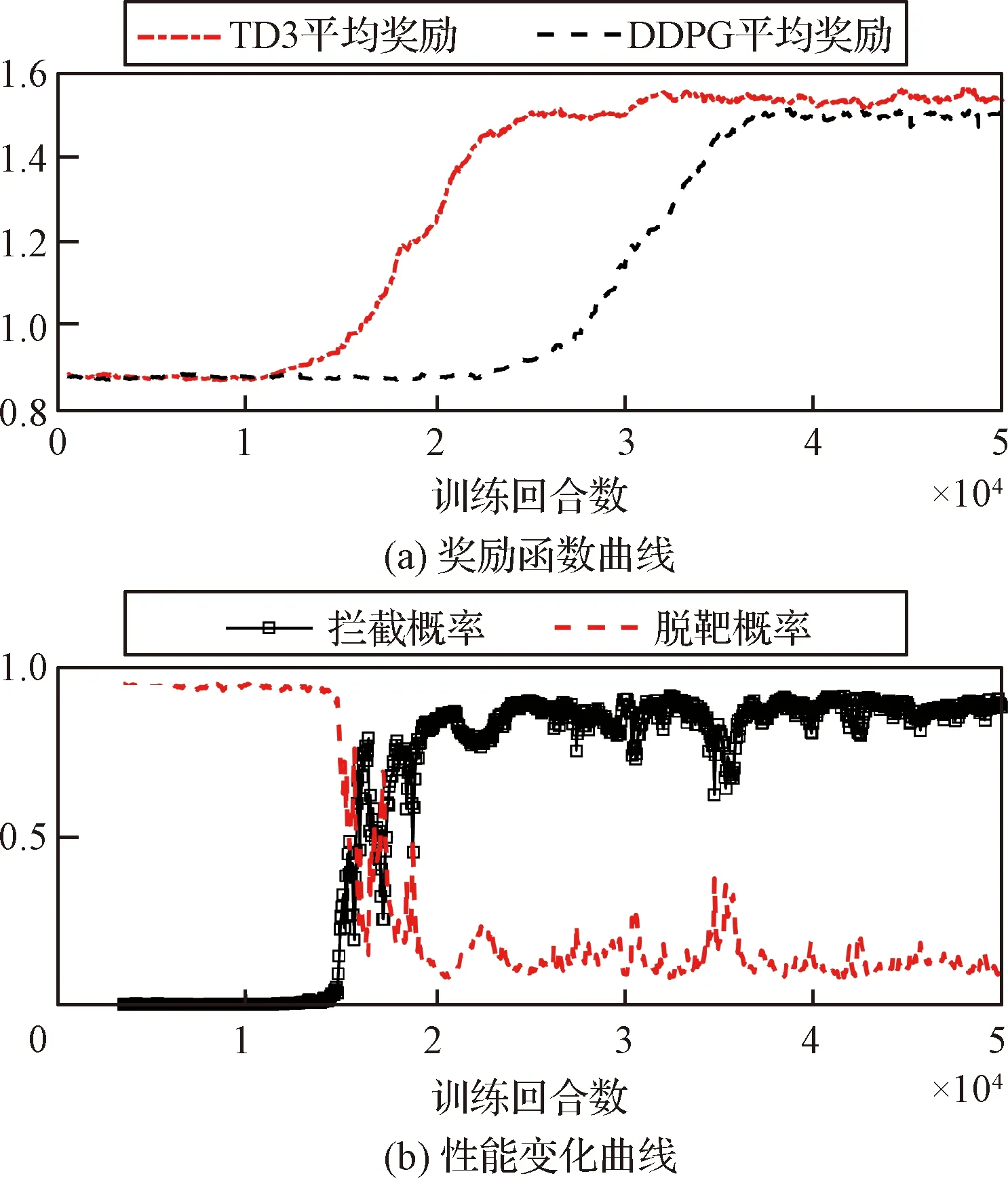
图5 训练曲线Fig.5 Training curves

3.2 测试过程

为测试算法训练所得拦截弹制导策略的性能，选用第41600回合所得到的策略网络模型，开展如下测试。

1)训练场景下的测试

首先在与训练场景相同的参数设置下开展测试，验证制导策略的有效性。为了充分测试深度强化学习制导律的性能，以式(28)所示的PN和APN导引律作对比，本文进行了1000次的蒙特卡洛仿真。图6给出了这三种制导方案的脱靶量散布，表4则给出了脱靶量散布的统计特性。

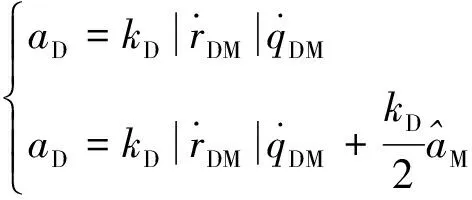
(28)

综合图6和表4可以看出，相对于PN和APN两种制导律，基于TD3的制导策略脱靶量更小。考虑到当前末端拦截弹多采取直接碰撞来袭目标的杀伤方式，显然较小的脱靶量更利于实现这种碰撞杀伤。此外，方差的数值彰显了本文制导策略在面对不同交战条件时性能的平稳性，不会出现过大波动。

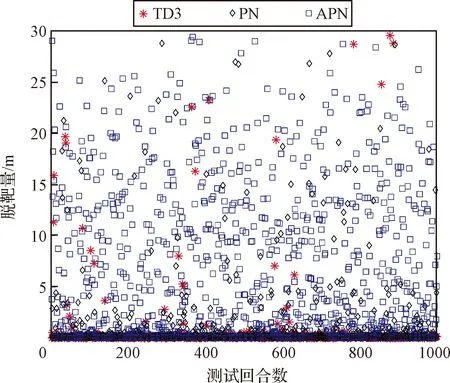
图6 不同导引律脱靶量Fig.6 Miss distances under different guidance laws

2)未学习场景下的测试

本小节将强化学习训练所得到的制导策略应用于多种未学习场景，并开展蒙特卡洛仿真实验，以验证该策略的鲁棒性和泛化能力。测试主要分为三部分。第一部分是测试制导策略应对不同初始航向误差时的性能。改变的取值范围，经过1000次蒙特卡洛仿真后所得不同制导策略的性能对比如图7所示。第二部分为测试当来袭导弹的机动模式改变时，本文制导策略的性能。将进攻弹的机动模式改为正弦机动，而非训练时所采用的方波机动，即：

(29)

此时的蒙特卡洛仿真结果如图8所示。第三部分测试则是减小进攻弹的机动频率。由横向位移的计算公式Δ2可知，当机动频率降低时进攻弹的横向位移会增大，即拥有更大的机动范围。此时三种制导策略的性能表现如图9所示。

图7 目标方波机动时性能对比Fig.7 Performance comparison of square wave maneuvering targets

图8 目标正弦机动时性能对比Fig.8 Performance comparison of sinusoidal maneuvering targets

由图7可见，在面临不同的初始航向误差时，相对于PN和APN，本文所提出的深度强化学习制导律均具备更高的拦截概率、更低的脱靶几率。进一步观察图7可以发现，本文制导策略的优势在较大时更加显著，即该策略能够应对更大的初始航向误差。以上分析说明本文所提出的末段制导策略可以降低对拦截弹中制导精度的要求，这在一定程度上有助于简化拦截弹中制导律设计。

图9 目标不同机动频率下的拦截概率Fig.9 Interception probabilities after changing the maneuvering frequency

综合图8和图9的仿真结果，可以看到无论来袭导弹的规避机动模式发生怎样的改变，基于TD3算法的制导策略相对于另外两种均具备更好的性能表现。进一步观察图9可见，随着目标机动频率的降低即机动范围的增大，TD3策略相对于PN和APN的优势趋于显著，这说明它不仅能够克服拦截弹自身的初始航向误差，同时能够有效应对来袭导弹较大范围地规避机动。以上分析验证了本文所设计的深度强化学习制导律能够在多种复杂工况下保持优异的性能，具备良好的鲁棒性和泛化能力。

4 结 论

本文提出了一种适用于大气层内拦截高速机动目标的深度强化学习制导律。将拦截交战运动学模型描述为马尔可夫决策过程，并设计了合适的训练场景、状态空间、动作空间和网络结构，分别引入奖励函数整形和随机初始化来提升算法的训练速度及最终策略的鲁棒性。仿真结果验证了本文制导策略的可行性。相对于PN和APN，本文方法脱靶量更小、性能表现更为稳定并降低了对中制导精度的要求，在多个未学习场景下的测试结果彰显了此策略良好的鲁棒性和泛化能力。此外，该制导策略对计算能力要求较低，便于在弹载计算机上运行。