天梯动力学与控制研究进展

关英姿，文梓达，汪小卫，张烽，崔乃刚

(1.哈尔滨工业大学航天学院，哈尔滨 150001；2. 中国运载火箭技术研究院研究发展部，北京 100076)

0 引 言

太空电梯(后文简称“天梯”)是一种通过攀爬器沿绳索往返运动将有效载荷从地球表面运送到太空的新型天地往返运输系统。相比于运载火箭、航天飞机等运载器，天梯具有低成本、快速、安全、可靠、高效的特点，颠覆性地改变了现有进入空间的方式。因此，天梯的成功部署和使用必将引起航天运输领域革命性的变革，是未来进行大规模空间开发和确保空间优势的重要保障手段。

天梯的起源最早可追溯到1895年Tsiolkovsky提出的“赤道通天塔”的构想。60余年后，Artsutanov提出了现代天梯的概念，此后这一概念被反复提及并不断完善。然而限于当时没有一种材料的强度能够满足天梯绳索的要求，天梯技术的研究并没有广泛开展。直到1991年碳纳米管材料的出现，使天梯的建造成为可能，于是20世纪90年代末掀起了天梯技术的研究热潮，这一时期学者们主要对地球赤道天梯的总体构建方案、各子系统方案以及建造和运行天梯面临的技术挑战等进行系统研究，随后也出现针对月球天梯的研究。

国际太空电梯联合会(International Space Elevator Consortium，ISEC)是致力于促进天梯开发、建设和运营的组织，从2010年起ISEC每年赞助一项关于天梯的重点主题研究，对天梯的总体架构和发展路线进行了详细的阐述，并给出了天梯模拟器的软件设计。2019年ISEC报告中提出了多级天梯的概念，多级天梯基于许多已有技术，有望使天梯比原计划提早实现。近两年ISEC报告针对未来空间任务对运载能力和规模的强大需求，讨论运行在银河港内的太空电梯技术。

天梯是空间系绳的应用之一，其本质属于超长绳系系统，是由延长绳系卫星系统发展而来的。但是天梯系统的绳索长度远大于绳系卫星的绳索长度，绳索本身的柔性特性往往不可忽略，因此天梯系统的部署和运行中存在的由绳索柔性引起的动力学问题更为复杂。此外，对于天梯动力学研究还需考虑攀爬器运动对绳索运动特性的影响。可见天梯动力学研究对于了解和掌握天梯系统的动力学特性至关重要，是研究和部署天梯系统的前提和基础。

近十年来,各国学者已从天梯力学原理、天梯系统可行性研究、天体总体方案构建过渡到天梯运行动力学和天梯部署动力学的研究。本文首先对天梯系统的组成和天梯初始部署方式进行简要的介绍；其次，针对天梯初始部署和运行中存在的复杂动力学与控制问题，分别从天梯动力学建模、天梯稳定性、天梯绳索振荡、攀爬器运动引起的绳索振荡及振荡抑制、天梯初始部署动力学五个方面分析归纳天梯动力学与控制的发展状况，最后结合目前天梯动力学与控制研究存在的难点及问题，提出后续的发展方向。

1 天梯系统的组成及初始部署形式

一个完整的地球赤道天梯系统如图1所示，主要包括地面锚节点平台、绳索(典型情况绳索长度可达10km)、攀爬器以及天顶锚。绳索与地球同步旋转，靠地球引力和离心力的共同作用，使天梯保持在铅垂位置。

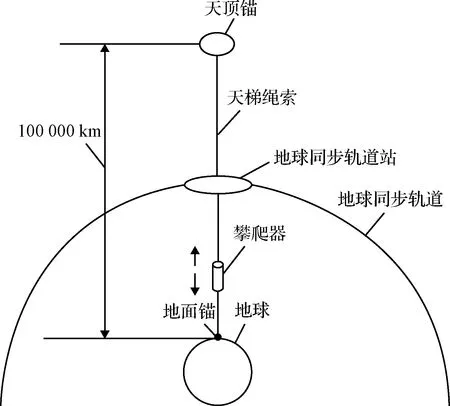
图1 天梯系统的组成Fig.1 Components of the space elevator

在NASA创新先进概念研究所(NIAC)资助下，Edwards针对天梯系统总体方案开展了大量工作，阐述了天梯系统建立的必要性，研究了天梯系统的构建方案、系统各组成部分的功能和质量的确定等问题。此外，文献[26]和[27]针对地面锚节点平台和天顶锚进行了专门讨论。

1.1 天梯绳索

绳索作为天梯系统的重要组成部分，是决定天梯系统规模的关键，因此在天梯概念提出后,研究者最先对构成天梯系统的绳索进行了大量研究，主要涉及绳索长度、绳索截面轮廓、绳索质量的计算以及绳索材料的选择等。

对天梯绳索进行受力研究，得出绳索在地球同步轨道处所受拉力最大的结论，于是从绳索各截面等应力的角度考虑，采用绳索横截面积从地球同步轨道处向两侧逐渐减小的设计。定义了绳索的锥度比(地球同步轨道处的绳索横截面积与地表锚点处的绳索横截面积之比)来表示绳索横截面积的变化，研究表明,在天梯绳索长度一定时，绳索锥度比取决于绳索材料的强度密度比。为避免地表锚点处绳索横截面积过大，绳索材料需要具有极高的强度密度比。Edwards假设绳索材料强度为130 GPa，密度为1300 kg/m，计算得到绳索的锥度比为1.5，这使得部署天梯成为可能。

碳纳米管一直被认为是最有潜力的天梯绳索材料。目前单个碳纳米管的强度已达到200 GPa，然而将碳纳米管合成一定尺寸的带状天梯绳索十分困难，目前最好的结果是强度达到9.6 GPa，密度为1850 kg/m，这与Edwards研究中所假设的材料性能还有很大差距。可见制备强度足够的天梯绳索仍然是目前建造天梯最主要的挑战之一。

1.2 攀爬器

攀爬器的本质是一种带有攀爬装置的航天器，主要用于运送有效载荷。Edwards的研究报告首次从用途、结构、供能等方面详细阐述了攀爬器。2013年ISEC报告针对系绳攀爬器的研究状况进行了总结。

攀爬器主要有以下3种用途：(1)用于对初始绳索进行加固。天梯初始绳索部署完成后，由攀爬器携带与绳索相同的材料沿绳索移动，对绳索进行加宽加厚，实现绳索的加固。(2)用于运送有效载荷。天梯系统投入使用后，可以由攀爬器携带有效载荷运送到任意轨道高度。(3)用于绳索修复。攀爬器将配备传感器，以检测系绳上的孔洞和撕裂，并配备设备进行维修。针对不同的任务类型，要求设计不同类型的攀爬器，文献中给出了6种不同类型的攀爬器，每种攀爬器具有各自的特点，并且供能方式也可能不同。

为实现攀爬器沿天梯绳索移动，Edwards给出了攀爬器的履带和滚轮设计，其中履带用于攀爬器抓附绳索，滚轮用于攀爬器在绳索上的移动。而Smitherman给出了不同的设计方案，攀爬器通过电磁悬浮，不与绳索接触。

攀爬器的移动需要对其供能，目前提出的可用能源包括：太阳能、光束能源(激光、微波等)、沿绳索传输的能源(电力、振动)以及攀爬器器载储能(化学能、电池/超级电容器、核能)。为避免能源传输中断，在攀爬器运输有效载荷时，应选择无线的能源传输方式对其进行供能，如激光或者太阳能。2013年ISEC报告中总结了激光供能和太阳能供能的优势与不足，认为采用两种供能方式的混合设计是最优的攀爬器供能方案。

当攀爬器穿越大气层时，可能会受到外界环境的影响(大风、闪电、暴雨等)而造成损坏。因此有学者提出在40 km高度以下需对攀爬器作保护，他们设计的保护盒能够将攀爬器与外界环境隔开，起到有效的保护作用。

按照ISEC报告的研究结果，攀爬器的设计要求为：自身重量约为6 t，携带的有效载荷质量为14 t，攀爬器能够实现每天发射，一周的时间可到达GEO轨道。研究者认为，当前技术能够满足上述要求，可实现攀爬器的设计与生产，保证未来天梯系统的运行。

1.3 天梯的部署方式

天梯系统的构建中绳索展开是天梯系统成功部署的关键。Edwards提出的地球天梯单向展开构建方案如图2所示。此外，Edwards还提出了双向展开的天梯构建方案。

图2 天梯系统单向展开构建示意图[5]Fig.2 One-way deployment and construction of the space elevator[5]

单向展开是指绳索自地球同步轨道处单向向下展开，并且随着绳索的展开，航天器需要携带绳索一起向上移动以提升轨道高度，保证整个天梯系统的质心在地球同步轨道之上。待绳索下端到达地面后锚定，航天器到达远端成为天顶锚。双向展开则是绳索在地球同步轨道处同时向上向下展开，绳索完全展开后，绳索下端在地面锚定，而后地球同步轨道处的航天器向上移动到达绳索上端作为天顶锚。

研究表明，单向展开只需要对向下展开的绳索进行控制，更容易实现天梯绳索的部署，但展开耗时较长。双向展开需要同时控制绳索的上下两端，控制较为复杂，但是部署时间短。考虑到部署时间与消耗燃料的关系，目前研究中对于天梯初始绳索构建中多采用了双向展开的绳索部署方式。

2 天梯动力学研究

前文所述的绳索从地球表面开始延伸到地球同步轨道以上高度的天梯称作完全天梯(Full space elevator，SE)，也是通常意义上的天梯。2009年Woo提出了部分天梯(Partial space elevator，PSE)的概念。与规模为10km长的完全天梯不同，部分天梯中连接主卫星和子卫星的绳索长度较短(通常为10～100 km)，攀爬器在两卫星之间的绳索上爬行。因此部分天梯部署所需时间更短、成本更低、安全性更高，对于绳索的强度要求也相对较低，同时也降低了空间碎片碰撞绳索的风险。以目前的技术来看，部分天梯更容易在近期实现。本文总结天梯动力学的发展状况，不仅包括完全天梯，还包括部分天梯。

2.1 天梯系统动力学模型

对于天梯来说，不同动力学模型的区别主要在于对天梯绳索的建模。常用的绳索模型包括刚性杆模型、集中质量模型和连续体模型。

1)刚性杆模型

刚性杆模型忽略绳索的弹性，将天梯绳索简化为刚性杆，包括考虑杆的质量和不考虑杆的质量的模型。刚性杆模型是最简单的天梯动力学模型，容易得到运动方程的解析解，但其精度较低，仿真得到的结果与实际偏差较大，一般用于对天梯绳索动力学特性的初步研究，如天梯稳定性的研究和天梯绳索展开动力学特性研究。

2)集中质量模型

集中质量模型是将天梯绳索离散化成若干段，将每一段的绳索质量集中于一个质点处，质点之间采用无质量刚性杆或者无质量弹簧连接，分别称为“刚性杆-珠点”模型和“弹簧-珠点”模型。图2示出了“弹簧-珠点”模型，该模型能够表示出绳索展开中绳索长度变化导致的绳索质量的变化，同时还能反映绳索的柔性特性，因此在天梯动力学研究中用于研究天梯部署动力学问题以及绳索振荡的抑制问题。Williams考虑到天梯绳索的变截面特点，基于集中质量的思想，建立了天梯绳索的丝带模型，丝带模型中各离散质点质量不同，其质量的变化反映了天梯绳索的锥化截面特性，更贴近天梯绳索的真实情况，是对弹簧-珠点模型的进一步发展。

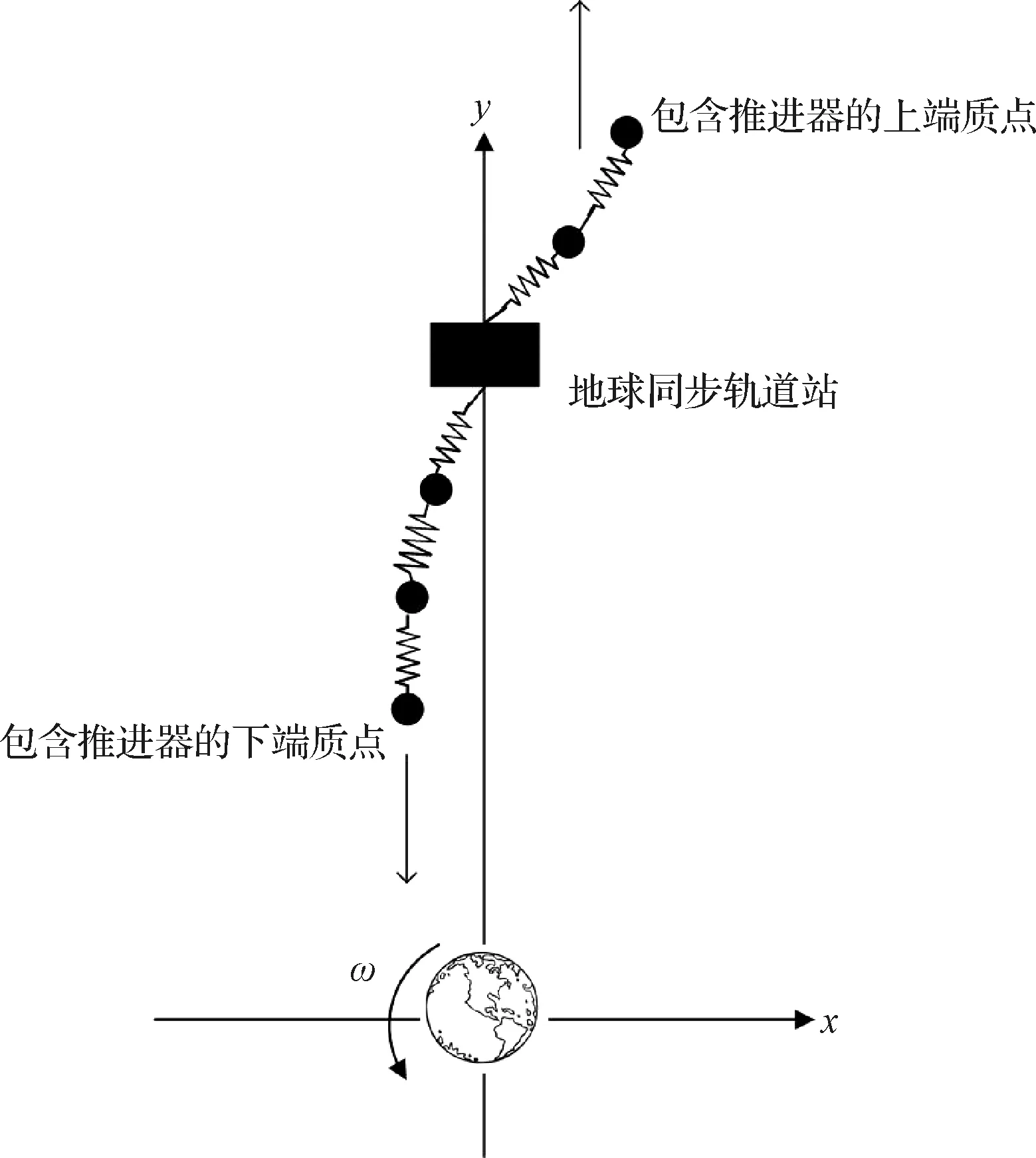
图3 弹簧-珠点模型Fig.3 Spring-bead model

3)连续体模型

连续体模型直接将天梯绳索作为连续的柔性体建模，其形式是由一组偏微分矢量方程表示的数学模型。连续体模型虽然最能反映天梯绳索柔性特性，是一种较精确的数学模型，但是求解中需要用假定模态方法或有限差分方法对偏微分方程进行离散，模型求解较为复杂，计算量庞大。目前采用连续体模型进行的天梯动力学研究主要集中在天梯完全展开后绳索振荡的研究上。

此外，早期在对天梯稳定性的初步研究中，出现过考虑绳索弹性但不考虑绳索质量的模型，该模型中天梯简化成一个质点通过一个长度为的不可伸缩的弹性绳索与地球赤道上的某点连接。为叙述方便我们将该模型称为无质量弹性绳索天梯模型。

2.2 天梯运行动力学研究状况

对于完全天梯来说，天梯运行动力学是指天梯绳索已经完全展开释放并且地面锚已锚定后的天梯动力学，即初始部署完成后的情况。对于部分天梯亦指绳索已完全展开。

1)天梯稳定性研究

由于地面锚已锚定，因此此时的天梯稳定性是指天梯的姿态稳定性，即天梯系统在其静平衡点附近的姿态运动稳定性。Beletskii等将天梯简化为由一个质点和一条无质量柔性绳索组成，绳索的下端固定于地球赤道面内地球表面某处，另一端与质点松散连接。建立了描述天梯在赤道平面内运动的第一类拉格朗日方程，给出了质点与绳索紧连接条件，在此基础上应用相平面方法研究了对应6个不同参数区域静平衡位置的运动稳定性，得到了静平衡位置运动稳定性条件同质点与绳索张紧连接条件完全一致的结论。

文献[35]仅研究了天梯在静平衡位置面内运动的稳定性问题。而王振坤对天梯稳定性的研究同时考虑了面内运动和面外运动。基于小角度运动假设，对建立的赤道天梯两自由度非线性动力学模型进行简化，应用线性稳定性定理对其拓扑等价的线性化系统的平衡点进行稳定性分析，得到天梯系统在平衡点附近具有渐进稳定性特征的结论。

2)绳索本身的振荡问题

绳索振荡是天梯系统的动力学特性之一，许多学者采用模态分析的方法研究绳索的振荡问题。Cohen等将天梯绳索采用一组可容许的基函数离散，并利用拉格朗日方程推导离散系统的运动方程，在假设横向振荡和纵向振荡解耦的情况下分别对两种振荡形式进行了模态分析，得到了给定绳索特性下天梯的纵向振荡和横向振荡的频率和相应的振型。Ohkawa等采用有限元方法对天梯绳索的连续体模型进行离散，分析了带有远端配重的绳索的横向和纵向振荡，发现远端配重能够减小绳索自由端的位移。此外文献[38]推导了保证系统稳定情况下配重质量满足的不等式关系。

文献[37]和[38]在研究绳索的振荡时均没有考虑空间环境的变化对绳索动态特性的影响，而在实际中天梯系统处于复杂的太空环境中，温度、辐射等因素都可能会导致绳索的振荡。Otsuka等假设天梯系统处于平衡状态，考虑温度对杨氏模量的影响，采用绳索的集中质量模型研究了温度变化对天梯系统动力学特性的影响。研究表明，温度变化会导致绳索的膨胀和收缩进而产生科氏力,导致绳索的纵向振荡和竖直方向上的拉伸和收缩。

3)攀爬器运动产生的振荡问题

天梯系统在轨运行期间，需要利用攀爬器进行有效载荷的运输，而攀爬器在绳索上运动产生的科氏力会引起绳索的振荡。因此，需要对攀爬器运动引起的振荡进行研究。

国内外学者针对这一问题进行了大量研究，如表1所示。为了突出攀爬器的影响并简化研究问题，研究中均忽略绳索本身产生的振荡。Cohen等采用考虑绳索质量的刚性杆模型，研究单个攀爬器在绳索上匀速向上或向下运动对天梯绳索天平动的影响。研究表明攀爬器向上或向下运动都会导致绳索的天平动，其中向下运动导致的振荡幅度更大，并且攀爬器引起的绳索振荡是在平衡位置附近的无阻尼振荡。而Lang利用广义绳系物体仿真系统(Generalized tethered object simulation system, GTOSS)对天梯进行时域模拟研究，获得了攀爬器向上运动并考虑空气动力载荷时绳索动力学响应和绳索内应力的数值结果。研究中向上运动的攀爬器的运动方式包括加速减速运动、突然刹车等。研究发现当攀爬器加速和减速运动时对绳索的纵向振荡影响更剧烈。

表1 攀爬器产生的振荡问题研究状况Table 1 Research status on oscillation caused by climbers

Williams和Ishikawa等采用集中质量绳索模型，并且考虑了天梯绳索变截面特性，研究了单一攀爬器以不同速度在绳索上匀速运动对绳索振荡的影响。研究发现速度的增加会导致绳索横向振荡幅度的增加，并且速度和绳索横向振荡振幅之间不为线性关系。文献[42]计算得到攀爬器向上和向下运动引起的绳索振荡周期大约为5天，与Cohen等得到的结果基本一致。文献[34]和[42]中还研究了攀爬器质量对绳索运动的影响，攀爬器质量的增加会导致绳索振荡幅度的增加，但不会影响振荡的周期。

Ohkawa等采用天梯绳索的连续体模型推导了单一攀爬器在绳索上运动时的运动方程，并将运动方程表征为一个分布参数系统，对攀爬器以恒定速度运动时天梯绳索的横向振荡进行了模态分析。

王振坤采用天梯绳索的刚性杆模型，并通过力来控制攀爬器的运动，研究了攀爬器以半正弦函数加速再匀速最后以半正弦函数减速的运动时，系统面内横向振荡角度随时间的变化和科氏力随时间的变化，研究表明攀爬器运行产生的科氏力是造成系统振荡的外部激励，并仅在赤道平面内对系统造成扰动，极限残余振荡角度幅值在10度量级。

上述文献中使用了两种攀爬器模型，一种是用攀爬器上方和下方的绳索的长度来表示攀爬器的位置，用攀爬器上方/下方系绳长度的变化率代表攀爬器沿系绳的移动速度，称作攀爬器的运动学模型。另一种是通过力来控制攀爬器的运动，根据攀爬器在轨道坐标系中的当前位置定义两个矢量，通过对两个矢量进行计算判断攀爬器所在的绳索位置，通过攀爬器的位置反映攀爬器的运动，称作攀爬器的动力学模型。Williams基于两种攀爬器模型对采用运动学攀爬器模型和动力学攀爬器的天梯系统进行了天梯系统的模态分析，结果表明两种不同攀爬器模型下天梯系统的模态分析结果基本一致，可见对于研究攀爬器运动对天梯绳索振荡的影响，攀爬器运动学模型的精度满足要求。

对于部分天梯，也有针对攀爬器产生的振荡问题的研究。Woo等建立了考虑绳索质量的部分天梯的绳索刚性杆模型，使用拉格朗日方程推导了部分天梯的非线性运动学方程，并在平衡位置附近对方程进行线性化处理得到数值解。文中分别研究了单一攀爬器以先加速后匀速最后减速在绳索上向上向下运动对绳索的动态响应，其中加速和减速期间速度以正弦函数形式变化。仿真结果表明，攀爬器的运动导致了部分天梯绳索的振荡，低频振荡占主导地位并且改变系统参数，如绳索的厚度和攀爬器的质量，对响应的性质影响不大。

而Sun等将部分天梯的绳索近似等效为柔性梁，利用绝对节点坐标公式建立绳索的动力学模型，并引入绳索分布质量和弹性影响，是一种高精度的动力学模型。针对主卫星和子卫星之间两种不同的空间相对位置，分别研究了单一攀爬器在绳索上向上和向下运动对绳索的动态响应。研究发现主、子卫星的相对位置与攀爬器的运动方向相比对绳索的动态响应影响可以忽略。

4)攀爬器运动引起的绳索振荡的抑制

国内外学者主要针对部分天梯研究了攀爬器运动引起的振荡的抑制问题，如表2所示。研究中采用的天梯绳索模型包括刚性杆模型和利用绝对节点坐标法建立的高精度有限元模型。其中，刚性杆模型不考虑绳索质量，将整个系统按照多体系留系统进行处理。有限元模型与刚性杆模型相比，精度更高，文献[49]中引入可变长度的模型来反映攀爬器沿着绳索的移动以及绳索在末端卫星上的展开和收回。

表2 攀爬器运动引起的绳索振荡抑制研究概况Table 2 Research status on oscillation suppression of cable caused by the motion of climbers

学者们分别针对单个攀爬器和多个攀爬器在天梯绳索上运动进行了振荡抑制的研究。对于单个攀爬器，文献[45]和[49]中攀爬器以恒定速度沿绳索向上和向下运动，研究了攀爬器速度对系统天平动的影响，系统的振荡幅度随攀爬器速度的增加而增加；研究了在攀爬器运动的同时展开端体对系统天平动的影响。文献[47]和[48]研究了单个攀爬器在绳索上以可变速度运动的情况。

Shi等研究了绳索上有三个攀爬器的情况，其中中间的攀爬器静止不动，两端的攀爬器可沿绳索上下移动。作者研究了两端的攀爬器以不同的组合方式运动时对绳索振荡的影响。研究表明攀爬器同时向相反方向移动的天平动幅度小于攀爬器同时向相同方向移动的天平动幅度。

绳索振荡的控制中选取的控制输入包括绳索的张力、攀爬器的速度和加速度。文献[45]针对三体绳系系统，选择攀爬器下部绳索所受张力作为控制输入，采用滑模控制律对张力进行控制。研究表明这种控制策略对抑制攀爬器的振荡非常有效。文献[48]分别采用攀爬器上部绳索所受张力最小的最优控制律和攀爬器移动时间最小的最优控制律,研究基于天梯系统哑铃模型和连续体模型的绳索振荡的抑制问题，结果表明,采用高保真连续体模型和简单的哑铃模型获得的天梯的动态性能基本一致，高保真模型更适用于验证由哑铃模型提出的控制策略。同时，文献[46]选择移动的攀爬器加速度作为控制输入通过找到攀爬器速度的最佳轨迹，最小化运行时间的成本函数。文献[47]选择攀爬器上端绳索长度变化率和绳索总长的变化率作为控制输入，采用与攀爬器和子卫星相对摆角、摆角变化率以及绳长变化的线性组合的控制律对其进行控制。文献[46]指出，所提出的速度控制比文献[45]中提出的张力控制有效，同时速度控制能够转化成张力控制。

为了提升天梯的运输效率，Li等提出了一种具有平行绳索和多攀爬器的部分天梯设计。当两条绳索上的攀爬器运动相同时，平行绳索的部分天梯可以按照一般的部分天梯进行研究。文献[50]中研究发现当多个攀爬器的瞬时运动不同时绳索会发生碰撞，可能加剧部分天梯的天平动，因此采用平行绳索的设计需要对攀爬器的运行轨迹进行优化以避免两根绳索之间的相互碰撞。在此基础上，文献[51]针对平行绳索的部分天梯提出了最小化攀爬器上端加速和最小化系统总摆动的最优控制策略，其中系统的总摆角最小化通过控制攀爬器的速度实现。研究表明，该控制策略在提升运输效率的同时也对平行天梯末端体的天平动起到较好的抑制效果。

2.3 天梯部署动力学研究状况

天梯的初始部署是通过绳索展开实现的。针对天梯系统初始构建过程，研究者主要研究了以下三个方面的问题：1)天梯系统的轨道稳定性问题；2)天梯绳索展开动力学与控制问题；3)天梯绳索展开过程中燃料的消耗问题。

1)天梯系统的轨道稳定性问题

天梯绳索的初始部署是十分困难的，难点之一是绳索展开过程中天梯的轨道可能是不稳定的，因此许多学者对天梯锚定前绳索展开中的轨道稳定性问题以及轨道保持问题进行了研究。

Mantri基于绳索展开过程的动力学仿真对天梯初始部署中的轨道稳定性进行了研究。为了研究绳索质量对展开过程的影响，分别采用不考虑绳索质量的哑铃模型和考虑绳索质量的刚性杆-珠点模型对天梯进行动力学建模，假设绳索从地球同步静止轨道同时向地球和远离地球的方向恒速展开，展开过程中推力器的推力大小相等、方向相反。文中定义天梯轨道偏心率小于等于0.01时，认为轨道是稳定的。从仿真结果中发现，展开过程中当绳索长度达到9×10km时轨道就不稳定了，因此无控条件下长度为10km的天梯绳索无法全部展开，可能坠落到地面。Mantri利用有质量和无质量绳索天梯动力学模型得到的天梯展开过程中质心随绳长的变化以及面内摆角随绳长的变化十分相似，证明了完全可以采用不考虑绳索质量的简化模型来研究天梯绳索初始部署的轨道稳定性问题。

Nicola等采用减少能量动量方法(Reduced energy momentum method, REMM)评估天梯径向相对平衡点的稳定性。首先采用刚性模型，推导出当哑铃卫星两质量间的距离大于轨道半径的0.63569倍时，哑铃卫星径向相对平衡位置将失去稳定性，即轨道不稳定。随后，采用连续质量绳索模型研究了相对径向位置稳定性问题。研究结果表明,连续体模型的天梯系统在展开过程中是不稳定的，可以通过在地球静止轨道上增加卫星使系统在展开过程中稳定，并且卫星的质量随着绳索长度的变化而改变。

Noboru等对天梯绳索已全部展开但绳索下端未锚定情况下天梯的轨道保持问题进行了研究。假设部署过程中燃料没有消耗，忽略天梯系统天平动的影响。文中设计了一条参考轨道，使天梯及其质心在保持地球静止轨道速率的情况下沿地球静止位置垂直上升。采用推力控制天梯使其能够跟踪参考轨迹，同时采用线性控制稳定参考轨迹。数值仿真验证了所提出的轨道控制策略的有效性，但是由于该控制策略基于较为简单的哑铃模型，同时没有考虑部署过程中燃料的消耗带来的质量变化，与实际情况存在较大差距，仍然需要后续进一步的深入研究。

2)天梯绳索展开动力学与控制问题

目前天梯绳索展开动力学控制方面的文献较少，公开发表的文献均是针对双向展开方案进行仿真研究的，对绳索展开中的动力学行为、绳索展开控制方式的研究并不深入。

Lang研究了绳索无控展开时的情况，发现如果在绳索展开阶段不对绳索进行控制，会造成系统质心轨道高度不断降低，最终导致绳索坠毁，部署失败。随后Lang提出了分阶段展开控制方案，将绳索的展开部署分为初始阶段、中间阶段、大气进入阶段和末阶段4个阶段。在中间阶段对上端体进行水平和垂直方向速度控制。文中仅给出了初始段和中间段的仿真结果，仿真结束时下端绳索长度已达35×10km。

Yamagiwa等建立天梯绳索的集中质量模型，选择基于展开速率的控制方式对天梯绳索的展开过程进行研究。设计了两种展开控制方案。方案1中,上下端体展开速度均沿铅垂方向，且绳索展开速度与相应端体的速度相同并保持恒定。方案2中,绳索的展开速度是变化的，上下端体铅垂方向的速度由设定的绳索张力阈值来控制，并控制端体水平方向位置保持在±250 km范围内。仿真结果表明，两种展开控制方案均能实现绳索的展开。其中，前者展开过程绳索最大横向振荡可达300 km。后者绳索最大横向振荡可达700 km。

3)天梯绳索展开过程中的燃料消耗问题

日本静冈大学Yamagiwa教授的团队对天梯绳索展开过程中燃料消耗问题进行了研究。发现适当控制绳索展开速度可以减少消耗推进剂的质量。但是研究中的上下端端体质量并未包含展开过程需消耗的燃料质量，也没有考虑燃料消耗带来的端体质量变化，研究条件与实际相差较大，会导致仿真结果与实际有出入;也没有讨论绳索振荡导致的天梯无法成功展开的问题。因此，在未来关于天梯绳索展开控制的研究中，需要研究绳索下端质量较大(包含消耗大量推进剂的质量)情况下绳索展开过程中燃料的消耗问题。

3 天梯动力学与控制研究的发展方向

3.1 天梯动力学建模方面

动力学模型是研究天梯初始展开部署动力学特性以及攀爬器运行期间天梯绳索动力学特性的基础。针对所研究的动力学问题特点选择适合的动力学模型是问题研究的关键。在早期天梯系统运行动力学研究中多采用刚性模型，初步得到了天梯系统基本的动力学特性。随后许多学者采用考虑绳索柔性的集中质量模型研究天梯系统初始展开部署中的绳索动力学特性。针对攀爬器运动引起的天梯绳索振荡问题研究多采用集中质量模型和连续体模型。

然而上述动力学模型在精细化上仍存在不足，为了更深入的研究天梯系统展开部署动力学特性和运行中攀爬器与绳索的耦合运动特性，未来需要建立更为精确的天梯初始部署动力学和运行动力学模型，主要考虑以下三方面：

1)考虑绳索截面形状特性的绳索动力学模型

按等应力设计的天梯绳索横截面尺寸是变化的，目前的绳索模型中仅考虑了绳索横截面积变化导致的绳索质量变化，而没有考虑绳索的形状特性。然而绳索截面形状特性对绳索不同方向弯曲刚度、截面惯性特性、扭转变形等均有影响，因此应建立考虑绳索截面形状特性的绳索动力学模型。

2)建立精确的攀爬器动力学模型

攀爬器是天梯系统的重要组成部分。目前对于攀爬器模型多采用运动学模型，也就是通过攀爬器前后绳长的变化来表示攀爬器的位置和速度。虽然也给出了攀爬器的动力学模型，但给出的各种力模型较粗略，因此需要针对攀爬器的运动机理建立更为精确的攀爬器动力学模型。

3)对空间环境力的精确建模

天梯系统动力学建模需要考虑许多环境因素，如太阳和热辐射，大气中的气动力，以及太阳和月亮的潮汐力等。其中最主要的环境力就是气动力。天梯初始部署中，绳索和绳索下端锚体将跨真空、稀薄大气、稠密大气层，大气特性变化显著，特别是稠密大气层内，气动力对绳索展开的动力学特性有较大影响，因此需对不同区域绳索和下端体的气动力进行精确建模。

3.2 天梯初始部署中的动力学与控制问题

天梯系统本质上是空间超长绳系系统，天梯绳索的展开过程中由于处于复杂的空间环境以及绳索的大柔性，因此表现出十分复杂的动力学行为，如果不进行有效控制，将存在非常复杂的动力学问题，可能会出现绳索打结、绳索振荡幅值过大、绳索其它部位先于绳索下端接触地面等情况。需要考虑绳索的大柔性、强非线性以及复杂空间环境等。为保证绳索可靠展开，需要研究绳索展开的轨迹规划问题，研究满足特定任务要求(摆角要求、展开时间要求等)，同时符合绳索本身的动力学约束、展开过程中绳索能承受的最大张力等过程约束和绳索上下端体终端约束条件下的最优展开轨迹问题。在此基础上研究最优轨迹的跟踪控制问题，探索新的控制方法，设计最佳的绳索展开控制律。

3.3 攀爬器运动引起的绳索振荡及振荡抑制问题

天梯系统从本质上来说是不稳定的，这是因为攀爬器运动过程中作用于攀爬器上的科里奥利力垂直于绳索，会引起绳索的天平动，若这种天平动不被很好地抑制，就会导致天梯系统的倾斜。目前对于单个攀爬器以不同速度、加速度方式运动导致的天梯绳索的振荡已进行了详细的研究，考虑到天梯的实际运行情况，未来的研究重点应是多攀爬器同时运动的绳索响应问题。此外，关于绳索振荡抑制问题，目前都是针对部分天梯进行研究的，但部分天梯的绳索长度远远小于完全天梯的绳索长度，绳索振荡的幅度远小于完全天梯，部分天梯抑制天平动的控制策略不一定适用于完全天梯，需针对完全天梯开展攀爬器运动引起的绳索振荡抑制研究。

4 结束语

天梯作为一种全新的空间运输概念，逐渐受到国内外学者的广泛关注。然而在天梯的构建过程中还有许多问题有待解决，其中天梯动力学与控制问题就是需要解决的重要问题之一。本文回顾了国内外天梯动力学与控制的研究状况，从天梯动力学建模、天梯运行过程中的绳索动力学、天梯初始部署动力学与控制等方面梳理了天梯动力学与控制中的关键问题，结合目前研究存在的难点及问题，提出了天梯动力学与控制研究的后续发展方向。

天梯系统是十分复杂的空间运输系统，虽然目前许多学者对天梯动力学与控制问题进行了较为深入的研究，对有望成为天梯绳索材料的碳纳米管料特性的研究也不断深入，但建造天梯仍然存在诸多困难和挑战，包括满足强度和尺寸要求的天梯绳索的制备、地面锚节点平台的选址建造、绳索展开控制、系统完全部署后的在轨稳定运行等问题。未来研究中需要针对上述难点问题进一步进行深入研究以寻找解决途径。