复杂禁飞区高超声速飞行器路径-轨迹双层规划

张 源，张 冉，李惠峰

(北京航空航天大学宇航学院，北京 100191)

0 引 言

高超声速飞行器具有机动突防能力强、全球快速响应等特点，已成为各国军事上关注的焦点。在再入滑翔段，高超声速飞行器需满足复杂的约束条件，禁飞区属于一种路径约束，禁飞区数量越多分布越复杂，轨迹规划的难度就越大。

在复杂禁飞区任务中，任务规划是一个包含决策层和物理层规划的混合问题。决策层指的是路径规划，即选择禁飞区的规避路线；物理层指的是轨迹规划，即设计高超声速动力学来满足再入飞行的各类约束。现有研究大都是针对物理层的，通过轨迹优化或设计横向制导逻辑规避禁飞区。在轨迹优化方面，主要包括伪谱法、凸优化、启发式算法等方法。原理是将禁飞区约束引入轨迹优化最优控制问题中，并用上述数值优化算法求解。前两种方法局部最优性和收敛性好，但由于禁飞区约束的强非凸性，算法多依赖于初始猜想。而启发式算法在全局搜索方面具有优势，但求解效率低下，难以实际应用。在横向制导逻辑设计方面，方法主要包括触角法、人工势场法、倾侧角符号反转法等。原理是在任务初值设定的前提下，基于上述方法使飞行器横向机动，从而规避禁飞区。在横向制导逻辑基础上，闭环制导律具有良好的可解释性和鲁棒性，在工程中应用广泛。为了提升闭环反馈的实时性，有学者通过推导解析解的方式设计制导律。Yu等以能量为自变量，推导了滑翔弹道解析公式，并基于该公式规划倾侧角符号的反转序列，使飞行器能够规避多禁飞区。但当飞行器进行大范围横向机动时，动力学非线性强，解析公式往往误差较大。

上述两类方法在针对复杂禁飞区规避任务时均存在问题。由于高超声速飞行器在任务规划时有多种绕飞路线选择，而轨迹优化方法强依赖于初始猜想，横向制导设计依赖任务初值设定，不具备决策能力。因此，本文将决策层的路径规划引入轨迹规划中，提出了复杂禁飞区路径-轨迹双层规划模型，通过组合优化的方式，使算法不依赖任务初值，提升轨迹的全局性能。然而，高超声速动力学具有强非线性，路径与轨迹规划之间往往是强耦合的，计算复杂度高，难以直接求解，因此如何对双层规划进行解耦协调是求解该问题的主要难点。

本文将上述耦合问题简化为两层进行快速求解，上层为路径规划，下层为轨迹规划。对于上层规划，基于图建模将路径规划转化为有向图搜索问题，搜索路径的评价指标根据一种路径点跟踪制导律仿真计算得到，仿真采用简化的动力学替代轨迹规划，实现双层规划的解耦。对于下层规划，由于引入了路径点信息，轨迹规划模型具有能够分段解耦横纵向动力学的优点，因此解析推导了横纵向飞行剖面，每段横程范围小，减小了解耦误差，提出了大范围横向机动的高超声速飞行器半解析在线轨迹规划方法。本文实现了物理层与决策层的融合规划，提高了轨迹的全局性能，对提升飞行器的自主决策能力具有指导意义。

1 高超声速飞行器复杂禁飞区规避路径-轨迹双层规划问题建模

考虑高超声速飞行器在再入滑翔段具有大范围的横向机动能力，可以根据不同路径进行禁飞区规避。上层规划根据禁飞区的分布构型布置路径点，从能量较优的角度优选路径点序列，进行路径规划。下层规划则基于上层规划优选得到的路径点序列，在轨迹经过路径点的前提下，设计合理的横纵向飞行剖面，得到飞行器的再入滑翔轨迹，以满足再入滑翔的过程约束、终端约束和禁飞区约束。

在双层规划中，上层规划反映能量消耗的路径优选指标(最小控制力)需要根据下层动力学仿真计算得到，同时下层规划的路径点目标由上层规划决定。该双层规划问题在相互影响中最终做出满足条件的决定，得到可行的飞行轨迹。在数学上，该双层规划模型可写为如下形式：

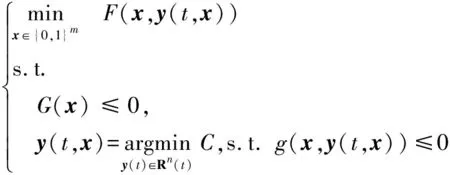
(1)

式中：为由0/1变量组成的向量，表示路径的选择；为当前路径下飞行轨迹变量组成的向量，是时间的函数；：{0,1}×()→是上层规划的目标函数，它是由下层轨迹规划结果反馈上来的；∈为常数，即下层规划无优化目标，得到合理的可行解即可；：{0,1}→{0,1}′,：{0,1}×()→′()分别为上层和下层规划的约束集，包含等式约束。其中,为0/1变量维数,为轨迹变量维数,′为上层约束集的维数,′为下层约束集的维数。

1.1 复杂禁飞区规避上层路径点规划模型

(2)

式中：=1表示弧(,)包含在该路径中；=0表示弧(,)不包含在该路径中。当某一条路径确定后，可转化成一系列的路径点约束。

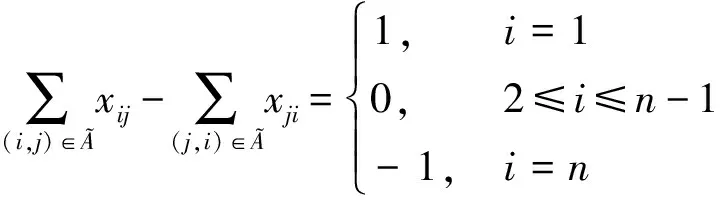
(3)

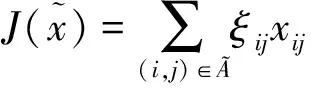
(4)

因此，给出以下上层规划模型：

(5)

其中，由于高超声速飞行器飞行状态、控制量的不同和严格的物理约束，即使同一条弧(,)，在不同路径中的值也不同，且无解析表达式。因此需要通过下层轨迹动力学仿真得到轨迹后计算得到。

1.2 高超声速飞行器下层轨迹规划模型

飞行器再入滑翔阶段需满足的前提条件包括动力学约束、路径约束、控制量约束和终端约束，也包括禁飞区约束和上层规划输出的路径点约束。

根据球形旋转地球假设，飞行器动力学模型表达式如下：

(6)

上述各式是对时间进行微分所得，式中：为地球中心到飞行器重心的径向距离；和分别为对应的经度和纬度；为飞行器相对于地球的速度；为航迹倾角；为航迹偏角；为倾侧角；为地球旋转角速度；为重力加速度；为飞行器质量；其中航迹偏角是速度向量在当地水平面的投影与正北方向的夹角，顺时针方向旋转为正；和分别为升力加速度和阻力加速度，其表达式如下所示：

(7)

式中：()为大气密度，它是海拔高度的函数；=-,为地球半径；为飞行器参考面积；为攻角；为马赫数；(,)和(,)分别为升力系数和阻力系数。

轨迹的能量消耗指标定义为：

(8)

作为上层评价当前路径的指标。式中：为横向加速度，,分别表示飞行器到达路径点和时的时间。该指标为横向分配的最小控制力，是反映无动力滑翔飞行器能量消耗的重要指标。由式(8)可以看出，受飞行器每个时刻的飞行状态影响，在轨迹得到前无法预知，所以在上层规划中需要通过下层动力学仿真得到路径指标。

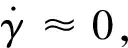
除了上述传统的约束，在本研究的飞行任务中还存在地理约束，即禁飞区约束和上层规划传递下来的路径点约束。

定义禁飞区为无限高的圆形区。禁飞区的圆心位置和半径预先确定。如果飞行轨迹上各点(,)到第个禁飞区圆心位置(,)的大圆距离大于相应的半径，则认为满足第个禁飞区约束，=1,2,…,’，’是禁飞区的总数，即：

(9)

飞行器的路径点约束为上层规划中搜索得到的路径点序列，由于路径点为虚拟设定的，因此该约束为软约束，目的是限定飞行器绕飞禁飞区的路线。当∃使得=1，=1,2,…,时，路径点包含在路径中，作为路径点约束。假设表示路径点约束，(,)为对应的位置坐标，∈{1,2,…,}，路径点个数不固定，由上层规划决定，则该约束可表示为：

(10)

因此，下层轨迹规划即基于当前的飞行状态，找到每个时刻合适的倾侧角控制指令()，使得相应的飞行轨迹满足上述动力学约束、路径约束、控制量约束、终端约束、禁飞区约束和路径点约束。

1.3 路径-轨迹双层规划方法框架

为了求解上述模型，本文提出方法的技术路线图如图1所示。

图1 路径-轨迹双层规划方法框架Fig.1 Framework of the dual-level path-trajectory generation method

通过解耦双层规划模型，对上层规划和下层规划分别求解。根据双层规划模型，上下层的耦合点在于：1) 上层规划中路径评价指标与下层规划的高超声速动力学约束耦合；2) 下层规划中的路径点约束与上层规划的优化变量耦合。注意到路径评价指标只与横向动力学耦合，在路径规划中，用简化的横向动力学仿真替代轨迹规划，以计算路径评价指标，实现上层规划与下层规划的解耦。在上层规划得到最优路径后，将最优路径点序列作为路径点约束，根据精确的高超声速动力学约束，进行下层轨迹规划，实现下层规划与上层规划的解耦。通过这样处理，既可以考虑路径-轨迹的动力学耦合特性，使路径评价指标合理，也可以解耦双层规划以降低算法的复杂性。

在实际应用中，本文根据禁飞区分布构型构造路径点，建立有向图模型，将上层路径规划转化为一个图搜索问题。在对搜索得到的路径进行指标评价时，简化动力学，保留与路径评价指标耦合的横向动力学，用横向动力学仿真替代复杂的轨迹规划过程，使路径规划与轨迹规划解耦。其中，在横向动力学仿真时应用了一种解析的路径点跟踪制导律。在下层轨迹规划中，直接将最优路径的路径点序列作为轨迹规划的路径点约束，解耦上层路径规划，解析推导高超声速飞行器的横纵向飞行剖面，设计自适应剖面跟踪制导律，完成双层规划。

2 考虑高超声速动力学的上层路径规划方法

通过引入禁飞区分布构型，进行有向图建模，建立路径集，基于横向动力学仿真得到路径评价指标，为下层轨迹规划提供最优路径点序列。

2.1 禁飞区规避路径建模

根据任务环境中禁飞区的分布构型布置路径点，引入全局信息，建立有向图模型。在作者之前的工作中，提出了一种适用于高超声速飞行器禁飞区规避的图建模方法，具体建模方法详见文献[22]。本文基于上述图建模方法进行上层路径优选，这里简要列出图建模方法。

1)布置路径点

2)有向边连接

(1)连接起点与串行线第一个禁飞区的两路径点；

(2)连接串行线中相邻两禁飞区的各个路径点；

(3)连接串行线中最后一个禁飞区的两个路径点与飞行终点。

图2 连边规则示意图Fig.2 Schematic diagram of directed edges connection

3)遍历路径

该建模方法结合了高超声速飞行器转弯能力有限的动力学特性，可以包含飞行器可行的绕飞方式。同时，连边策略能够减少无效边的连接，进而避免组合数的急剧增加。

2.2 路径评价

由于有向图中路径是离散路径点序列形式存在的，不满足高超声速动力学，因此通过对目标函数有直接影响的横向动力学，基于一种最小控制力路径点跟踪制导律进行数值积分，计算路径指标。

由式(8)，上层规划的目标函数与横向加速度=sin相关，暂时无需考虑纵向运动和强非线性的气动方程，忽略地球自转，得到如下运动模型：

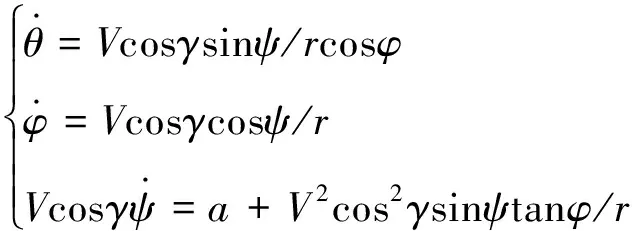
(11)

(12)

式中：和LOS表示与第个路径点的相对大圆距离和视线角；Δ=LOS-表示航向误差。

假设个路径点是按其相应到达时间,增加排序的，即,<,+1。在飞行器接近路径点时，到达时间可以近似为：

(13)

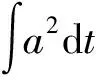
(14)

其中，拉格朗日乘子向量=[,,…,]可以解析求解，具体推导过程详见文献[18]。该制导律本质上是一种推广的自适应比例导引律，路径点跟踪精度高，且普适性强。

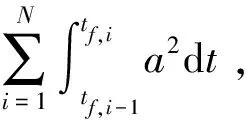
上述过程利用禁飞区分布构型，建立有向图模型进行路径规划，实现了高超声速飞行器路径-轨迹紧耦合，为下层提供合理路径点序列。

3 基于上层优选路径的高超声速飞行器分段半解析轨迹规划方法

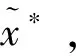
由于飞行器非线性较强，需合理分配横纵向飞行能力。其中，纵向剖面需要在满足滑翔过程约束和控制量约束的基础上，满足终端航程和状态量约束；横向剖面设计需要满足路径点要求和禁飞区绕飞要求，控制飞行能量在合理范围内。

3.1 高超声速飞行器纵向解析剖面规划

基于小量假设，将纵向运动与横向运动解耦处理，根据平衡滑翔条件确定阻力加速度-速度剖面，推导待飞航程解析式，求解剖面参数。在推导待飞航程预估闭环解析公式时，忽略因地球自转产生的哥氏加速度和离心加速度，得到如下所示运动公式：

(15)

令表示第段轨迹的预估航程，=1,2,…,。由航程的变化率：

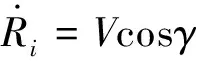
(16)

则航程计算公式为：

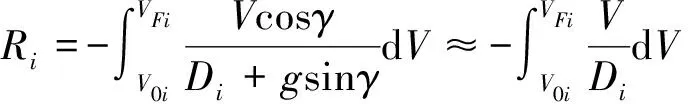
(17)

式中：0为每段初始速度；为每段终端速度；sin≈0; cos≈1。通过将阻力加速度表示为相对速度的函数关系()，便可根据式(17)直接得到航程解析表达式。

(18)

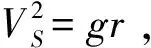
将式(18)代入式(17)中，可推导得到航程解析表达式如下所示：

(19)

根据每段轨迹的实际航程需求，可反解求得剖面参数/，确定阻力加速度剖面，=1,2,…,。则/为：

(20)

3.2 高超声速飞行器横向解析剖面规划

基于纵向航程预估设计的剖面，提出飞行器横程预估的解析表达式，令每段轨迹的横程为0，得到每段轨迹对应的倾侧角反转点，使得飞行器能够经过路径点。

由动力学方程(15)，在广义赤道的基础上，设,为小量，采用sin≈0, cos≈1, tan≈0的假设条件，可简化为：

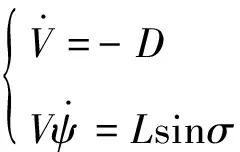
(21)

则：

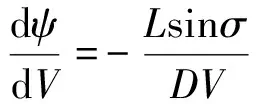
(22)

令每段倾侧角反转点速度为，初始倾侧角符号表示为()，=1,2,…,。则可得每段航迹偏角计算公式为:

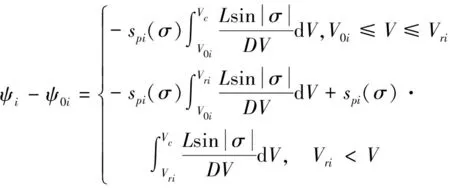
(23)

式中：为当前速度；0为每段航迹偏角初值，=1,2,…,。

在基于平衡滑翔条件设计剖面时，/参数给定，可得到参考阻力加速度对应的铅垂面内升阻比(/)≈/。由于剖面给定，因此飞行器实际升阻比可由下式计算得到：

(24)

当攻角变化不大时，可将的幅值近似为常值。则式(23)可简化为：

-0=

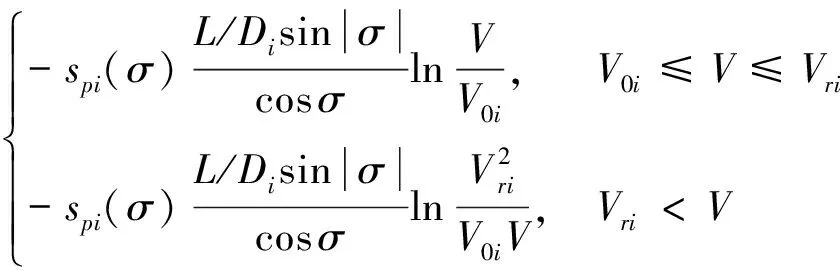
(25)

由每段横程的变化率：

(26)

式中：LOS为每段目标点的视线偏角，每段横向机动较小，可假设Δ为小量。将式(25)代入式(26)中，横程对速度的变化率为：

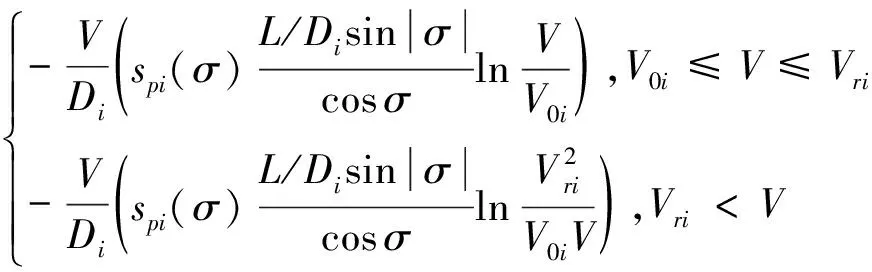
(27)

因此，可得如下所示的横程计算公式：

(28)

式中：为每段终端速度。

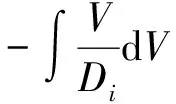
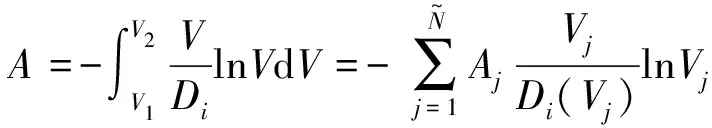
(29)

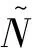
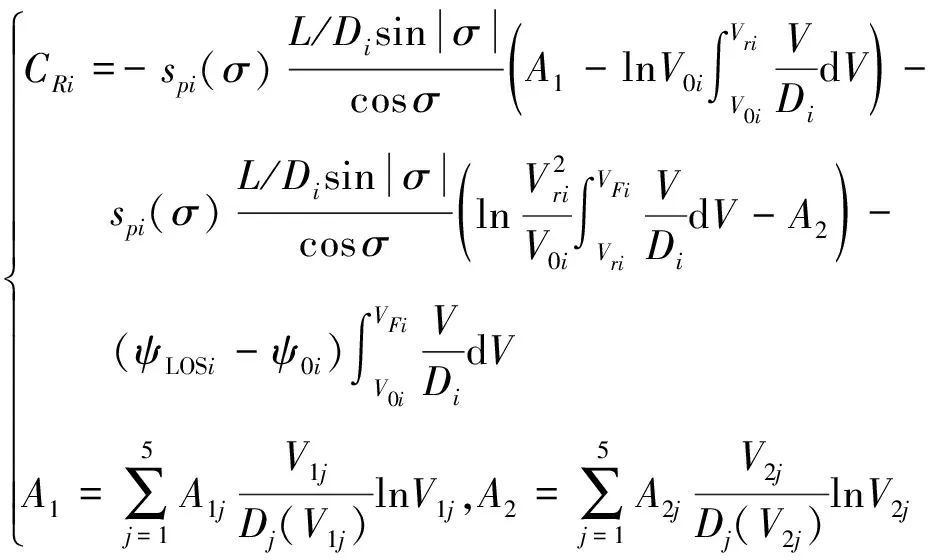
(30)

令=0，利用简单迭代法得到倾侧角反转点的位置，=1,2,…,。

3.3 横纵向解析剖面跟踪制导逻辑

根据剖面形式，设计自适应跟踪制导律，完成轨迹规划。飞行剖面跟踪制导逻辑具体如下：

采用倾侧角和攻角两个控制量，倾侧角为主控制量，攻角采用标称剖面以减小飞行器气动加热分布变化。倾侧角完成航程与横程的控制：幅值控制航程,符号控制横程。

1)纵程控制

采用“前馈+反馈”的控制策略完成整个再入过程阻力加速度剖面的在线跟踪，形式如下：

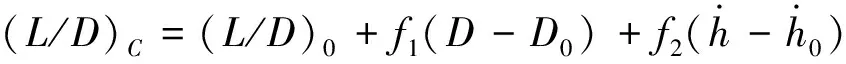
(31)

则倾侧角幅值指令：

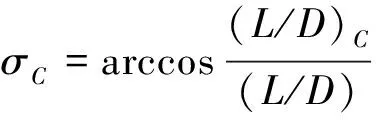
(32)

式中：(/)为飞行器实际升阻比。

2)横程控制

每段规划一个反转点，根据横程公式，式(30)，计算反转点位置，经过路径点。在最后一段轨迹，为更好的瞄准目标，采用航向瞄准误差作为横向死区，实现横程控制。

通过本方法，可以根据路径优选得到的路径点序列，将轨迹分段处理，基于小量假设进行横纵向解耦，解析推导横纵向飞行剖面。分段减小了横向机动带来的解耦误差，提高了剖面解析精度，实现了大范围横向机动的半解析轨迹规划算法。

4 方法实现

本节介绍高超声速飞行器复杂禁飞区的路径-轨迹双层规划方法的数值实现过程。整个双层规划的流程图如图3所示。具体实施步骤可总结为：

1)进行有向图建模，使用深度优先算法遍历飞行路径；

4)根据最优路径对应的路径点序列，分割滑翔轨迹，分配分段点速度值;

5)设定攻角剖面和初始高度，根据剖面跟踪控制律跟踪轨迹，计算倾侧角幅值指令;

6)在每段初始位置，根据横程预估解析表达式求解该段的倾侧角反转点,当到达最后一段初始位置时，切换为死区控制;

7)以速度到达终端速度作为停机条件，得到最终的剩余航程，依据剩余航程是否满足要求反向调整纵向初始高度和攻角剖面，完成下层轨迹规划;

8)输出上层路径优选的路径点序列和下层轨迹规划的飞行轨迹，即状态量及控制量，完成双层规划。

图3 方法实现流程图Fig.3 The flow chart for implementation

5 仿真校验

本节中应用本文提出的高超声速飞行器路径-轨迹双层规划方法求解一个复杂禁飞区规避的算例，以说明方法的有效性。

飞行器在任意初始航向角的滑翔过程中，需要避开5个圆形禁飞区。飞行器在经纬度坐标中的初始位置为(0°, 0°)，终点位置为(100°, 0°)。禁飞区约束的圆心经纬度坐标和半径见表1。

飞行器初始状态为：=7002 m/s，=60～70 km，=0°，指向第一个路径点。滑翔终端要求：>42 km，剩余航程150 km≤≤250 km，终

表1 禁飞区分布Table 1 Information of no-fly zones

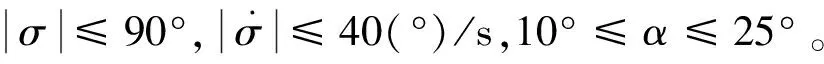
5.1 飞行器复杂禁飞区上层路径规划仿真

根据上层规划中的图建模方法，利用Python NetworkX库建立可视化网络模型，得到有向图模型如图4所示，图中数字表示各路径点序号。

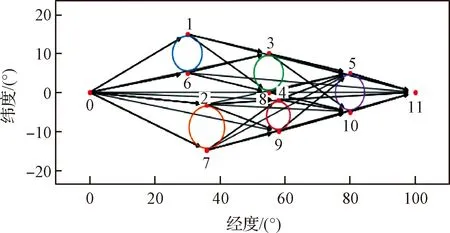
图4 算例有向图Fig.4 Directed graph for the numerical simulation

将遍历后的路径进行基于路径点跟踪制导律，即式(14)的仿真路径评价，排序得到指标最优的路径为[0,6,3,11]，指标为7764.61 m/s，该路径所对应的路径点坐标见表2。

表2 路径点优选方案Table 2 Information of waypoints

作为对比，基于Gauss伪谱法，利用MATLAB工具箱GPOPS求解此问题(求解时进行3次网格精化，网格精化的容差设置为0.0001)。图5～8给出了本方法仿真结果与最优参考的对比。

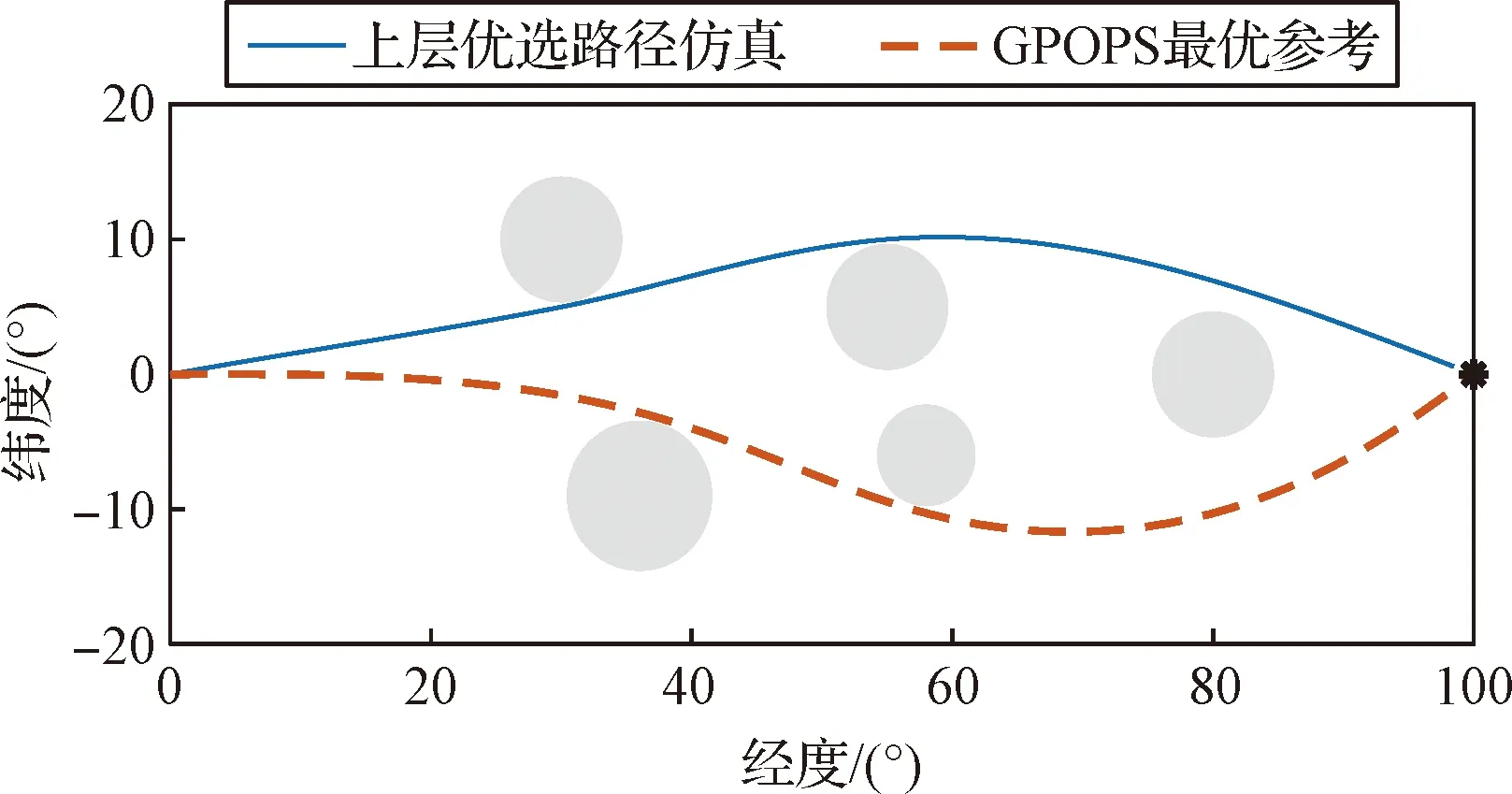
图5 轨迹对比Fig.5 Comparison of trajectories

图6 横向加速度对比Fig.6 Comparison of lateral accelerations

图7 航迹偏角对比Fig.7 Comparison of heading angles

图8 性能指标对比Fig.8 Comparison of performance indicators

图5对比了两种方法的轨迹，GPOPS选择的路径与本方法不同，这是因为伪谱法陷入了禁飞区带来的局部最优，对初始猜测有很强的依赖性。图6为横向加速度的比较，在轨迹后半段GPOPS得到的的幅值明显更大。通过积分，GPOPS的性能指标为23082.26 m/s，性能指标对比如图8所示，本方法优选路径的指标7764.61 m/s明显更优。从航迹偏角的对比图7也可以看出，GPOPS得到的航迹偏角变化更快，累积横程更大，导致能量消耗更多。因此，优化算法虽然可以保证局部最优解，但本文引用上层信息的路径优选方法考虑了不同路径对轨迹性能的影响，具有更好的全局性能。

5.2 高超声速飞行器下层轨迹规划仿真

由上层路径优选出的3个路径点(包含终点)，将轨迹分成3段，基于航程预估解析公式求解各段阻力加速度剖面参数/，每段待飞航程为两点间大圆距离，最后一段待飞航程设置为距离终点175 km。分配每段终端速度使得整个滑翔轨迹阻力加速度剖面光滑，得到纵向各参数。剖面跟踪过程中，在每段初根据横程预估式(30)求解得到每段的倾侧角反转点位置。得到横纵向飞行剖面各参数见表3。

表3 飞行剖面参数Table 3 Profile parameters

其中，最后一段横程控制切换为死区控制，所以无固定的倾侧角反转点。

将初始高度定为65700 m，攻角设置为13.10°，进行在线剖面跟踪制导。仿真结果如图9～13所示。仿真结果显示，以速度为停机条件，规划的剩余航程为175 km，实际跟踪制导后实际的剩余航程为174.81 km，误差仅为0.19 km(飞行总航程为11112 km，误差百分比为0.002%)，表明本方法的解析式具有很高的精度。

图9为飞行轨迹，2个路径点位置误差分别为14.76 km和12.88 km，由于路径点为软约束，允许误差范围大，因此该方法能够满足条件。图10为高度剖面图，终端高度为44.64 km，满足要求，且高度剖面光滑，没有出现轨迹震荡的现象。图11给出了倾侧角指令，仿真算例满足倾侧角幅值和角速率的要求。由图12航迹倾角的剖面看出，终端航迹倾角在-0.3°以内，可以满足平衡滑翔的软约束。图13给出阻力加速度剖面的跟踪效果，图中可以看出，实际剖面与标称剖面几乎重叠，跟踪效果显著，跟踪误差在10数量级，说明剖面设计合理可飞。图中毛刺产生原因是剖面更新带来的瞬时变化对跟踪控制律的影响。整个飞行过程中热流率峰值为825.82 kW/m，过载峰值为1.10，满足过程约束。

图9 飞行轨迹Fig.9 Flight trajectory

图10 高度-速度剖面Fig.10 Altitude-velocity profile

图11 倾侧角-速度剖面Fig.11 Bank angle-velocity profile

图12 航迹倾角-速度剖面Fig.12 Flight path angle-velocity profile

图13 阻力加速度剖面及跟踪误差Fig.13 Drag acceleration profile and tracking errors

蒙特卡洛仿真是检验算法鲁棒性的主要方式，对本节仿真的路径进行1000次蒙特卡洛仿真散布分析。考虑的不确定性参数见表4，其中风干扰为由高速-风速差值表得到的平稳风。

表4 蒙特卡洛仿真不确定性参数Table 4 The uncertain parameters of Monte Carlo simulation

在上述不确定性参数的影响下，轨迹规划算法得到的各终端指标满足情况见表5。为方便展示，其中50条轨迹规划结果如图14所示。

表5 蒙特卡洛仿真结果统计Table 5 Monte Carlo simulation results

图14 蒙特卡洛仿真飞行轨迹图Fig.14 Monte Carlo simulation of flight trajectories

可以得出，该轨迹规划算法对外界环境干扰具有较强的鲁棒性，各终端约束和过程约束基本可以满足。这些不确定性对解析剖面精度造成一定的影响，从而造成标称轨迹存在误差，在实际使用中可通过剖面实时更新来降低干扰的影响。

为了验证解析剖面的适应性，对该禁飞区场景的其他路径进行剖面计算并进行在线跟踪制导仿真，以速度为停机条件，规划的剩余航程为175 km，统计各工况制导精度见表6。

从表6中可以看出，本文提出的分段半解析方法对各路径的适应性较强，航程误差最大为3.45 km，误差百分比不超过0.03%，可以表明本方法的解析飞行剖面具有很高的精度。

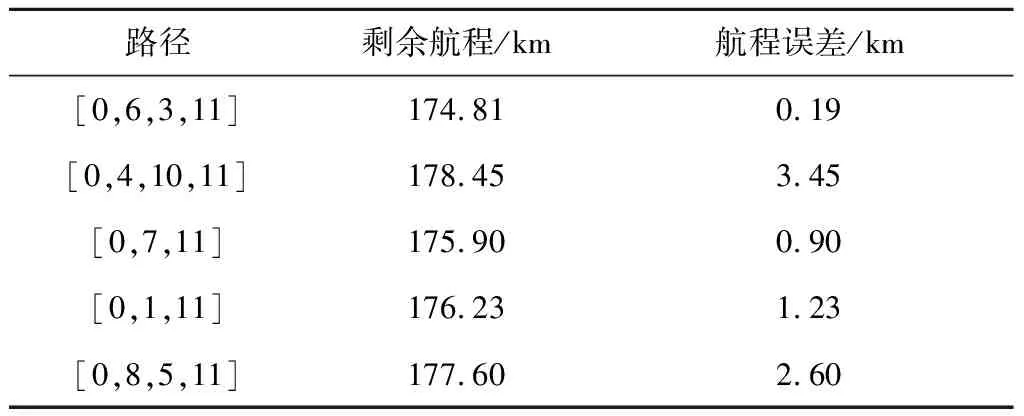
表6 不同路径剖面制导精度对比Table 6 Comparison of paths’ guidance accuracy

总之，将复杂禁飞区规避的轨迹规划转化为双层规划，引入全局信息进行路径的优选，提高了轨迹的全局性能；同时，根据上层优选路径点序列，得到分段解析飞行剖面，制导精度较高。本方法融合了路径规划和轨迹规划各自的优势，既能从全局性能需求出发选择合理的路线，又能得到满足各类约束的可行飞行轨迹。

6 结 论

本文实现了高超声速飞行器禁飞区规避上层路径选择与轨迹规划双层建模和快速求解。该方法提升了轨迹的全局性能，数值仿真表明此方法与不考虑路径选择的轨迹优化方法比，路径能量指标更优。此外，解决了大范围横向机动的飞行剖面解析难题，数值仿真表明该方法制导精度高，适应性强，满足再入滑翔过程各类约束。总之，提出的路径-轨迹双层规划方法是一种全局求解高超声速飞行器复杂禁飞区规避轨迹规划问题的有效途径。