空间机械臂辅助深层采样阻抗控制策略
聂佳伟,辛鹏飞,荣吉利,王 瑞,潘成龙,程修妍
(1. 北京理工大学宇航学院,北京 100081;2. 北京空间飞行器总体设计部,北京 100094;3. 齐鲁工业大学(山东省科学院)数学与统计学院,济南 250353)
0 引 言
月球资源具有巨大的战略价值,是人类社会长期可持续发展的重要支撑。通过深层采样分析月壤组成和结构,不仅能探查月球资源的分布情况,对将来月球基地选址也发挥着重要作用。
对于月球采样,不少学者已经做了很多研究。史晓萌等对月壤与采样机具间相互作用中的钻进负载进行了研究;梁磊等研究了小型采样器在月表低气压重力环境下浅层月壤的铲挖阻力预测及参数优选问题;凌云等提出一种由三个刚性臂和一个柔性臂组合、结构新颖的月壤取样器,并通过动力学响应确定了取样器的工作极限;卢伟等设计了一种重量轻、功效低、收缩体积小的卷簧式可伸缩月壤取样器,并通过理论分析、仿真及实验验证了取样器设计的合理性及振动法取样的有效性。然而,上述这些研究都着重对采样机钻取采样过程进行了研究,未对采样过程中机械臂的运动控制进行研究。在月球深层采样过程中,主要涉及到机械臂与复杂接触面的接触碰撞问题,在接触操作时,如何设计控制策略来使机械臂柔顺、安全地完成任务是该过程中最主要的问题。
针对类似复杂接触面机械臂的控制问题,不少学者已经进行过研究。王彬峦从协作型机械臂的碰撞检测响应和柔顺控制两个功能切入,提出了一套不依赖外部传感器的协作型机械臂碰撞检测、碰撞响应和柔顺控制策略。钱震杰根据赫兹接触理论建立了考虑摩擦的接触碰撞动力学模型,并对实际的空间机械臂模型做了仿真研究。危清清等提出了柔性机械臂辅助大负载空间舱对接的阻抗控制方法,并利用Adams-Matlab进行了联合仿真。莫洋等对空间机械臂辅助大质量舱体对接任务,提出了采用阻抗控制的方法,并通过Adams与Matlab/Simulink对接触过程进行联合仿真,证明了阻抗控制算法能够有效减小接触力。在这些文献中,不足之处在于模型比较简单,或者运动比较简单,文献[6]采用的是一个二自由度的机械臂系统,文献[8]和文献[9]中机械臂的运动相对比较简单,这些简单的模型和运动无法满足采样机械臂的任务需求,而文献[7]则没有涉及到机械臂的轨迹规划和控制问题。贾庆轩等对太空七自由度机械臂的碰撞问题进行了研究,对机械臂碰前轨迹进行了研究,并建立了碰撞动力学模型对碰撞过程进行仿真,但其研究中同样未涉及到对机械臂的控制。
由于空间机械臂辅助深层采样过程中,机械臂不可避免地存在与地面及孔洞的接触碰撞,这对机械臂控制精度以及采样任务完成带来了较大的挑战。为了减小深层采样过程中的系统振动,本文基于四自由度机械臂,建立了非光滑系统的精确动力学模型,提出了含碰撞问题的阻抗控制方法,实现了深层采样任务中机械臂的柔顺运动。首先,基于局部标架的刚体李群SO(3)方法对机械臂进行建模,通过梯形规划对机械臂的轨迹进行了规划,采用阻抗控制方法对机械臂进行控制,推导了李群SO(3)模型下机械臂关节空间与末端笛卡尔空间之间的雅可比矩阵,并且得到了两个空间的相互转换关系。其次,采用了锥互补方法计算接触力,相较于罚函数方法,该方法实行了非嵌入的原则,可以采用相对较大的时间步长进行计算,并且相较于罚参数将引起系统高频振动的缺点,锥互补方法描述的非光滑动力学能较为精确地处理刚性碰撞问题。最后,通过对控制参数进行调整,探究了不同控制参数对机械臂控制的影响,优化得到了合适的控制参数,从而能控制机械臂辅助完成深层采样的任务。
1 空间机械臂建模
1.1 机械臂介绍
空间机械臂是由多个关节和臂杆等机构部件组成,在空间零重力、微重力作用环境中进行工作的多体系统。本文针对一类四自由度机械臂进行了建模,并且忽略了机械臂的柔性,采用刚体单元对机械臂进行建模。
1.2 机械臂参数介绍
机械臂结构示意图如图1所示,~为机械臂结构长度,其长度见表1。
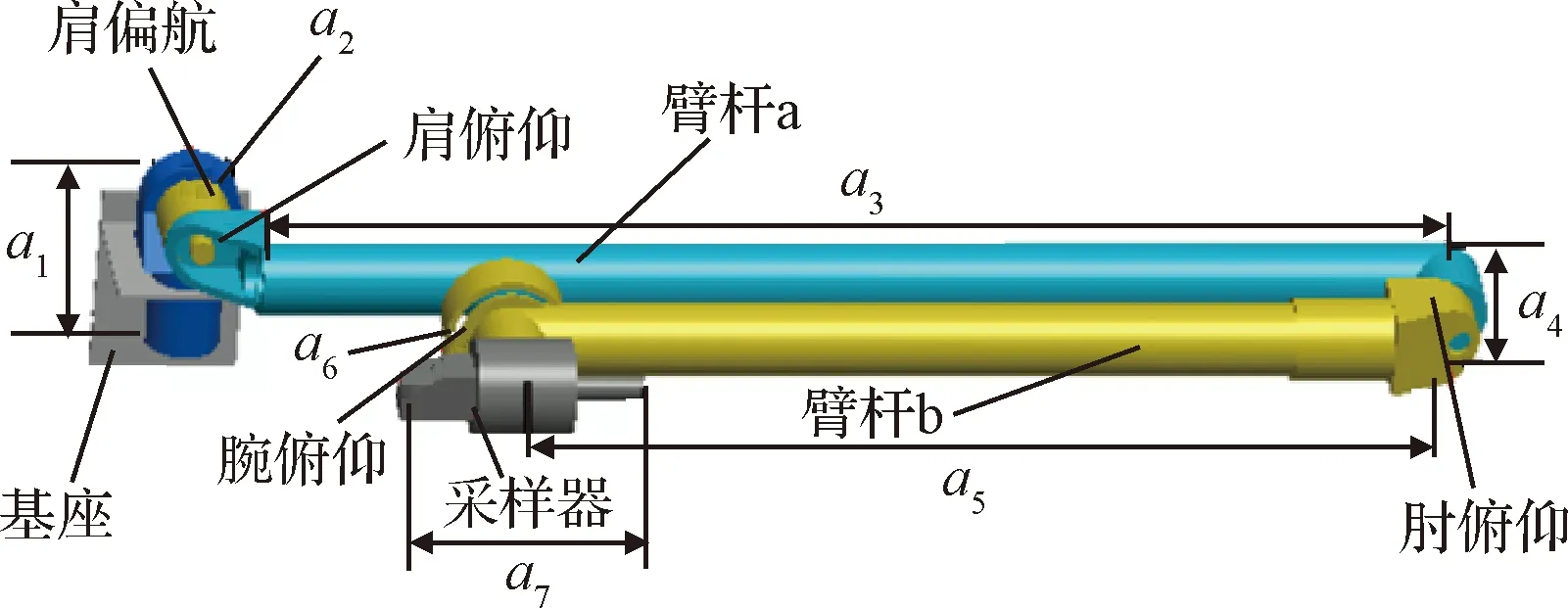
图1 机械臂结构示意图Fig.1 Schematic diagram of manipulator structure
在该模型中,机械臂线密度为=2000 kg/m,第一个机械臂的主转动惯量的三个分量为16.67 kg·m、8.35 kg·m、8.35 kg·m;第二个机

表1 机械臂结构长度数据Table 1 Structure length data of the manipulator
械臂的三个分量为183.33 kg·m、119.4 kg·m、119.4 kg·m;的三个分量为166.67 kg·m、104.17 kg·m、104.17 kg·m;的三个分量为33.33 kg·m、16.83 kg·m、16.83 kg·m。
1.3 李群SO(3)非光滑广义-a锥互补方法
本文采用局部标架的刚体李群SO(3)方法对机械臂进行建模,并采用非光滑广义-a方法进行求解,其动力学方程为:

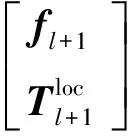
(1)
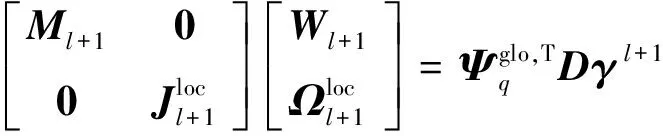
(2)
=
(3)

(4)
式中:+1表示第+1个时间步的变量,为质量矩阵,为转动惯量矩阵,loc表示连体局部坐标系下的变量,glo为全局坐标系下的变量。需要注意以下几点:
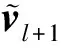

(5)
该映射将任意三维向量映射为三阶反对称矩阵;
2) 式(1)中,双边约束被放到了光滑的运动学方程中,这点对结果是不会有影响的,传统的广义-a方法在求解带双边约束的DAE方程时就具有与求解ODE方程相同的性质;

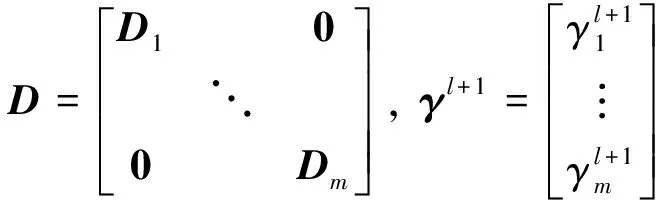
(6)
其中,为接触点个数,=[,,,],=1,2,…,,其中,可以通过间隙函数对广义坐标求导得到,而其他两项则可以在接触平面内任意选取;
4) 式(3)为双边约束方程,在该机械臂系统中,为旋转铰约束,其通过将两个臂上的接触点进行固定,并令两个臂上平行于转轴的单位向量,在全局坐标系重合实现:

(7)

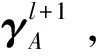

(8)

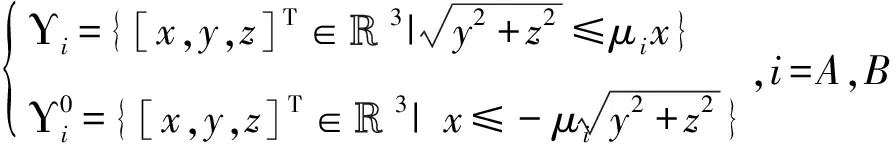
(9)
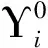
在该方法中,速度的变化被分为两部分,一部分是由加速度引起的光滑分量,另一部分是由碰撞等非光滑力引起的非光滑分量。其离散格式如下:

(10)

(11)
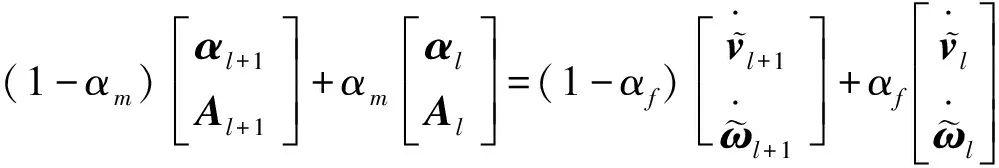
(12)

(13)

(14)
+1=+Δ+1
(15)

(16)
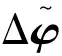
式(1)~(4)的求解方法可以参考文献[14],不过该论文中需要求解一个线性互补问题(LCP),而此处需要求解一个锥互补问题(CCP),因此,需要将其中的LCP求解器,替换为CCP对应的求解器。至于求解CCP的方法,则采用文献[15]中的加速投影梯度下降(APGD)算法进行求解。
2 位置型阻抗控制
2.1 机械臂关节空间与末端笛卡尔空间
在机械臂系统中,存在描述关节运动的关节坐标系和描述末端位置和姿态的末端笛卡尔坐标系等,由机械臂关节坐标系的坐标到机械臂末端位置和姿态之间的映射,称为机械臂的正向运动学;由机械臂末端位置和姿态到机械臂关节坐标系的坐标之间的映射,称为逆向运动学。
图2为机械臂关节坐标示意图,~为关节空间的四个关节角,从轴正方向看,顺时针方向为的正方向;从轴正方向看,逆时针方向为~的正方向。①~④为四个机械臂编号。通过关节坐标系,可以表示出第四个臂质心的位置及姿态,也就是机械臂末端笛卡尔空间的位置和姿态:
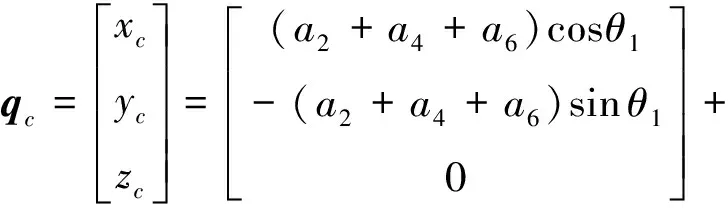
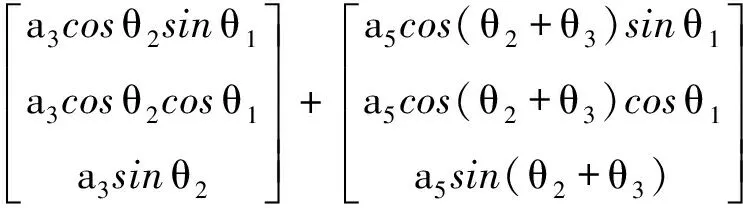
(17)
其中,为第四个臂质心的坐标,~均为机械臂长度参数。
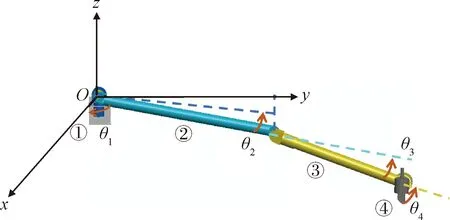
图2 机械臂四个关节角示意图Fig.2 Schematic diagram of the four joint angles of the manipulator
由于:

(18)


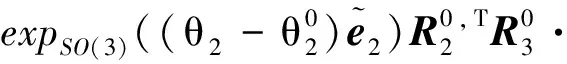


(19)
于是可以表示机械臂末端的姿态:
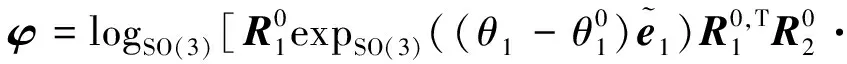
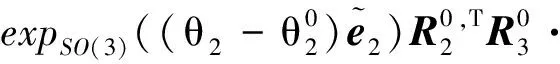
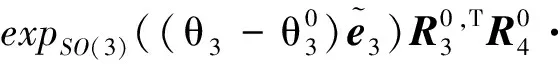
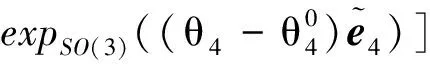
(20)
式(17)和式(20)可以统一表示为:

(21)
式(21)即为关节空间向末端笛卡尔空间转换公式。
将式(17)前两个分量进行化简可以得到以下两个关系:
sin+cos=cos+cos(+)
(22)
cos-sin=++
(23)
由式(23)可以得到:
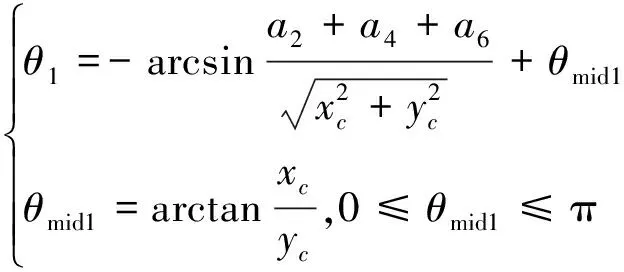
(24)
由式(22)和式(17)第三个分量可以得到如下关系式:

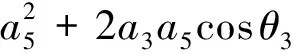
(25)
cos-(sin+cossin)=
sin
(26)
由式(23)和式(25)可以求得:
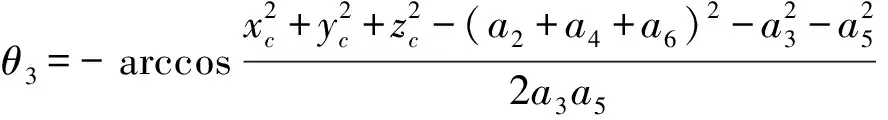
(27)
由式(26)可以求得:


(28)
由式(20)可以求得:

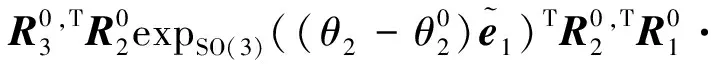

(29)
其最终角度需根据机械臂的实际运动情况进行选取。
2.2 机械臂笛卡尔空间和关节空间的雅可比矩阵
机械臂笛卡尔空间运动速度与关节空间运动速度之间的变换,称为雅可比矩阵。雅可比矩阵是关节空间速度向笛卡尔空间速度的传动比:

(30)
其中,=[]。
由式(17)和式(20)可以计算得到机械臂的雅可比矩阵:
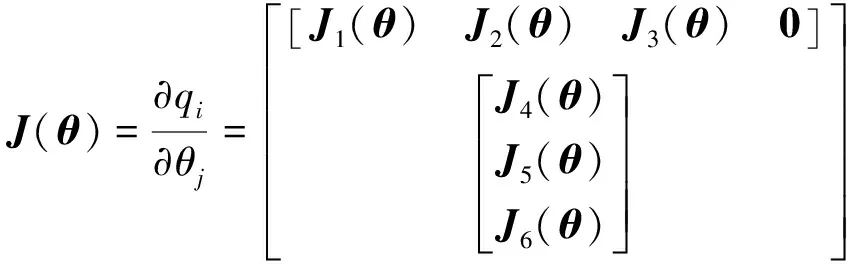
=1,2,3;=1,2,…,4
(31)
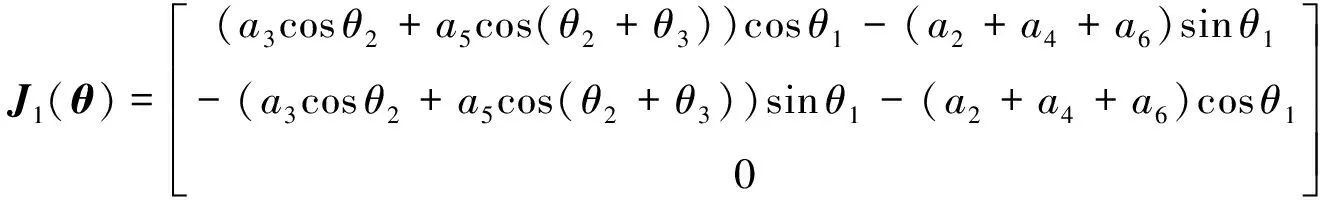
(32)
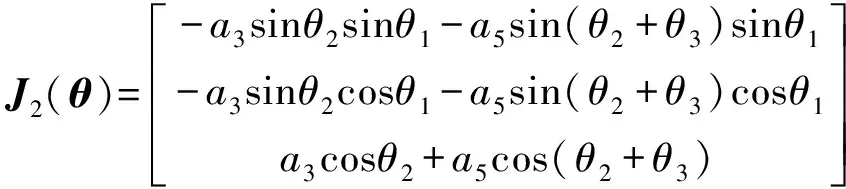
(33)

(34)
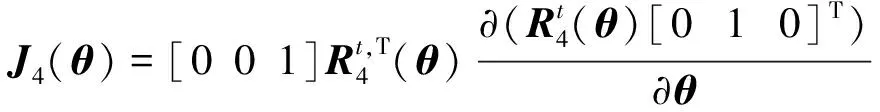
(35)

(36)

(37)
2.3 笛卡尔空间与关节空间的静力变换
机械臂笛卡尔空间与关节空间的静力变换在文献[12]中有详细介绍,此处简单介绍一下。机械臂在关节空间中的虚功,可以表示为:

(38)
其中,δ是机械臂在关节空间所做的虚功,=[]是机械臂关节空间的等效静力矩,δ=[δδδδ]是关节空间的虚拟位移。
同样的,机械臂在笛卡尔空间中的虚功为:
δ=δ
(39)
其中,δ为笛卡尔空间广义力的虚拟位移。
机械臂笛卡尔空间与关节空间的虚拟位移之间存在如下关系:
δ=()δ
(40)
其中,为机械臂的雅可比矩阵。
考虑到机械臂在笛卡尔空间与关节空间的虚功是等价的,由式(38)~(40)可得:
=()
(41)
2.4 位置型阻抗控制


(42)

图3 位置型阻抗控制流程图Fig.3 Flow chart of position-based impedance control
由于在李群的建模方法中,动力学方程中的外力即为广义控制力,因此在仿真的过程中,不需要计算关节空间的力或力矩。在实际的机械臂系统中,需要根据下式计算得到关节空间的驱动力:
=
(43)
然后就能够驱动机械臂进行运动。
3 空间机械臂辅助深层采样控制与仿真
3.1 机械臂与固定面接触仿真
对于图1所示的机械臂,采用速度梯形规划,令四个关节角度在6 s内从初始位置=[00 -π0]运动至=[-π/2 -π/6 -π/6 -π/6],初末时刻速度和加速度均为0,其轨迹规划结果如图4所示。

图4 机械臂与固定面接触问题轨迹规划Fig.4 Trajectory planning results of the manipulator contact with fixed surface

图5 机械臂初始构型图Fig.5 Initial configuration of the manipulator
在机械臂的仿真控制中,在=-0.2 m处增加了一个接触面,限制机械臂方向的运动,机械臂初始构型图及接触面模型如图5所示。机械臂与接触面的摩擦系数=0.2,分别使用位置型阻抗控制和位置控制对机械臂进行控制,其中位置型阻抗控制的控制参数为:

(44)
=4
(45)
=10000
(46)
其中,的前三个分量单位为kg/s,后三个分量单位为kg·m/s;的前三个分量单位为kg/s,后三个分量单位为kg·m/s;的前三个分量单位为kg/s,后三个分量单位为kg·m/s,为了方便,后文中这三个变量单位与此处保持一致,不再强调;为6阶单位矩阵。位置控制的控制参数为:
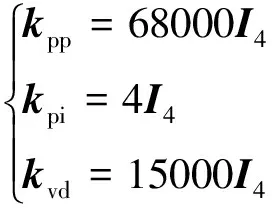
(47)
其中,为4阶单位矩阵。
机械臂末端位置和姿态随时间变化曲线如图6所示。相较位置控制,位置型阻抗控制更能够精确柔顺地控制机械臂沿着预期轨迹运动。

图6 机械臂与固定面接触情况末端位置和姿态随时间变化曲线Fig.6 Curves of the end position and attitude of the manipulator contact with fix surface
3.2 控制参数对机械臂柔顺控制的影响
在空间机械臂辅助深层采样的过程中,需要柔顺地控制机械臂沿着预期轨迹运动。为此,通过调节图3中PID控制方法的相关控制参数,比较不同控制参数对机械臂柔顺控制的影响,为机械臂控制参数的选取提供依据。
对于3.1小节中的算例,首先比较了不同对控制结果的影响,控制其他参数不变,分别计算了=/10和=10的情况,并与的情况进行了对比,机械臂末端位置与姿态对比结果如图7所示,可以发现,当取值较小时,机械臂运动的曲线会难以跟踪预期轨迹,而当取值较大时,机械臂在发生碰撞时会出现较大的碰撞力,并且会有明显的振动,由此可见,在实际控制过程中,应当取合适的值,从而使得机械臂能够柔顺地跟踪预期轨迹进行运动。

图7 不同kpp情况机械臂末端位置和姿态对比Fig.7 Comparison of the end position and attitude of the manipulator under different kpp conditions

同样的,可以确定中剩余参数的大致取值范围,见表2。
然后,比较了不同对控制结果的影响,控制其他参数不变,分别计算了=/10和=

表2 kpp各参数取值范围Table 2 Value range of each parameter in kpp
10的情况,并与的情况进行了对比,发现不同对控制结果的影响较小。
最后,比较了不同对控制结果的影响,令其他参数不变,分别计算了=/10和=10的情况,在计算过程中,出现了Newton迭代不收敛的现象,并且反复进行尝试,最终令=15000,若将的取值较大,则会出现迭代不收敛的情况,将=/10和=15000的情况进行了对比,机械臂末端位置与姿态对比结果如图8所
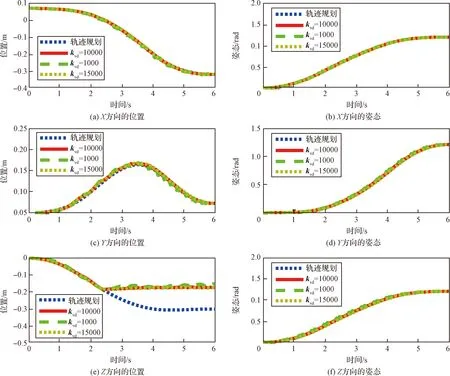
图8 不同kvd情况机械臂末端位置和姿态对比Fig.8 Comparison of the end position and attitude of the manipulator under different kvd conditions
示,可以发现,当取值较小时,机械臂在发生碰撞时会出现较大的碰撞力,并且会有明显的振动;而取值较大时,则会出现迭代不收敛的情况,因此,选取合适的对于机械臂的柔顺控制也发挥着重要作用。
进一步地,控制和不变,确定了中各元素的大致取值范围均为7500~16000。在实际应用中,,和应该结合具体问题具体分析,确保能够控制机械臂顺利完成任务。
3.3 机械臂深层采样仿真
为了实现对机械臂深层采样的情况进行仿真,对于图1所示机械臂,设计了如图9所示深层孔,孔圆心横纵坐标为(0.075 m,0.1 m),孔分为上下两层,上层半径=0.07 m,深度=0.1 m,下层=0.03 m,深度=0.1 m,接触平面位于=-0.2 m处,机械臂与接触面的摩擦系数=0.2。针对该深层孔,分别对两种工况进行仿真,一种采样深度浅,一种采样深度深。其中,采样深度浅的工况中,设定机械臂的采样深度比复杂孔深度浅;而采样深度深的工况则比复杂孔深度深,这样机械臂就由于孔深度的限制而无法到达预期位置,该工况是为了探究机械臂在与孔底部发生接触后是否继续向前运动。

图9 复杂深层孔模型Fig.9 Complex deep hole model
在接触检测过程中,首先需要计算检测点距离圆心的水平距离以及检测点前一时刻距离圆心的水平距离 0,然后根据判断和 0与半径的大小以及检测点与接触面的相对高度,就可以判断该接触点可能会与哪个面进行接触,具体接触检测流程如图10所示。
首先是采样深度浅的工况,机械臂初始四个关节角为=[0 0 -π 0],令其末端从初始位置运动至(0.075 m,0.1 m,-0.3 m)处,并令末端终止时刻姿态保持竖直。
机械臂的轨迹规划结果如图11所示,机械臂控制参数中,的六个参数依次为:2.55×10, 2.55×10, 4.25×10, 2.55×10, 2.55×10, 2.55×10;=4;=15000。
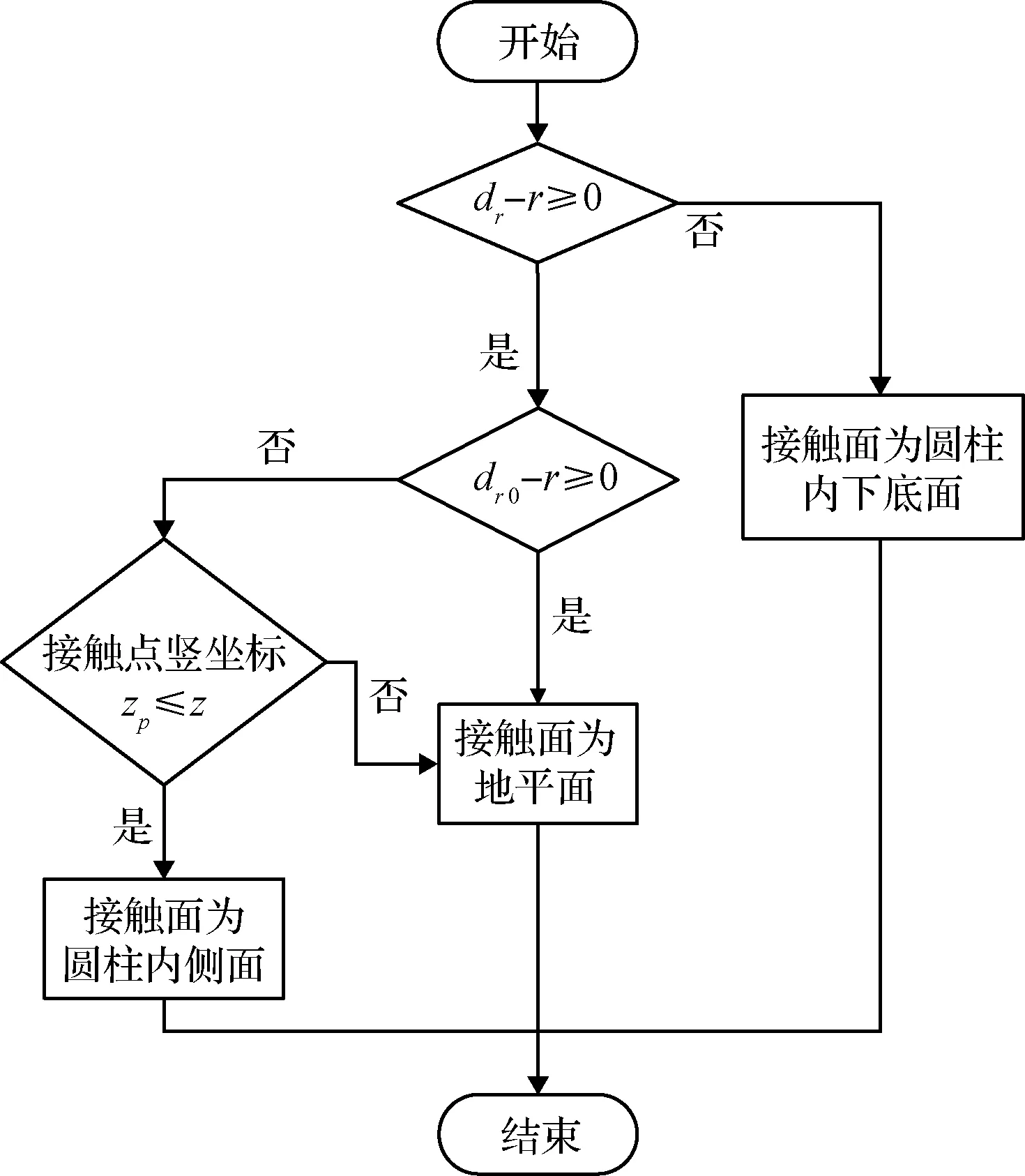
图10 圆柱孔接触面检测流程图Fig.10 Cylindrical hole contact surface detection flow chart
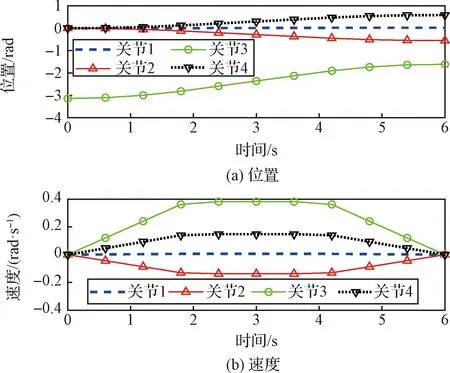
图11 机械臂深层采样情况轨迹规划Fig.11 Trajectory planning results of the manipulator for deep sampling
机械臂末端位置和姿态随时间变化曲线如图12所示。从这些图中可以看出,机械臂末端能够沿着目标轨迹运动至预期位置,实现深层采样的任务。
然后是采样深度深的工况,控制复杂孔的位置和形状不变,机械臂控制参数及与接触面摩擦系数不变,改变机械臂末端的终了位置,令其从初始位置运动至(0.075 m,0.1 m,-0.4 m)处,机械臂末端终止时刻仍保持竖直。
采用同样的方法对机械臂进行轨迹规划,并保持机械臂控制参数不变。
机械臂末端位置和姿态随时间变化曲线如图13所示。根据末端位置以及构型图可以看出,在=5 s时,机械臂末端已经与复杂孔底部发生接触,


图12 采样深度浅情况下机械臂末端位置和姿态随时间变化曲线Fig.12 Changes of the end position and attitude of the manipulator versus time in the case of shallow sampling

图13 采样深度深情况下机械臂末端位置和姿态随时间变化曲线Fig.13 Changes of the end position and attitude of the manipulator versus time in the case of deep sampling
无法继续向下运动,这与预期结果相符合,由此表明该阻抗控制能够实现对机械臂的仿真和控制。
4 结 论
本文采用刚体李群SO(3)方法建立了机械臂动力学模型,分别采用位置控制与位置型阻抗控制方法研究了含碰撞的机械臂轨迹跟踪问题。研究表明,位置型阻抗控制能够精准对施加在机械臂末端的力进行调整,使机械臂能够柔顺地沿着平面继续运动。通过调节PID控制器不同参数,发现和对控制结果的影响较大:取较小值时机械臂会无法精准沿着预期轨迹运动,取较大值时机械臂会产生较大的振动;取较小值时机械臂同样会产生较大的振动,取较大值时则会导致仿真的迭代不收敛。进一步探究,通过控制变量的方法确定了和的大致取值范围。基于上述建模与控制方法,针对采样深度浅与采样深度深两种工况,通过选取合适的控制参数,使得机械臂能够柔顺地辅助采样机完成采样任务。

