基于落角约束的偏置比例导引律的研究*
严鹏辉,刘刚,缪前树
(中国直升机设计研究所,天津 300300)
0 引言
直升机机载反坦克导弹一直在反坦克作战中发挥着重要作用。传统的比例导引律虽具有控制简单、过载变化小等优点,但是随着坦克主动防御技术的完善,以及正面和侧面装甲防护的加强,此时通过增大导弹落角并且控制落角精度来攻击坦克防护薄弱部位(如炮塔顶部等)宜为一种较理想的毁伤方式[1]。
对于导弹飞行末端带落角约束制导律的研究,主要是基于比例导引律的改进并结合现代控制理论形成约束条件[2-4]。影响导弹落角的方式有多种,如导弹初始高度、弹目距离等[5-6],而对导弹导引律的设计是最为关键的措施[7],如王利芳等[6]、林德福等[8]通过在导引律中添加重力补偿项,可以增大导弹的命中落角,但是落角提升的幅度有限,而且难以做到落角的精确控制。Zarchan[9]利用Schwartz不等式推导出弹道成型最优制导律,在控制能量消耗需求最小的同时,实现了落点与落角的双重约束;Ratnoo[10-11]对传统比例导引进行扩展变形,得到基于落角约束的两段变增益比例律;王广帅[12-13]将常值偏置项添加到比例导引律中,可以实现对目标的落角约束;高峰[14]对导引律做微分处理,提出一种基于落角约束的偏置比例导引律。
本文基于弹目碰撞三角形关系,借鉴文献[13,15-16]思想,考虑目标速度方向,研究了基于落角约束且无需精确计算剩余飞行时间的变增益偏置比例导引律;同时与弹道成型制导律、两段变增益比例导引律进行比较,分析三者弹道曲线、倾角、过载和控制能量消耗的区别;给出不同初始条件,进一步探究此制导律性能,对比了不同落角约束对导弹弹道、过载和控制能量消耗的影响。
1 弹目相对运动模型
如图1所示,M和T分别表示导弹和目标,vM,vT分别为导弹和目标速度矢量,与x轴方向夹角分别为θM,θT。vR为相对速度矢量,θR为相对速度矢量与x轴夹角,r为弹目距离,q为弹目视线角。为研究方便,本文中将角度的正方向定义为逆时针方向。
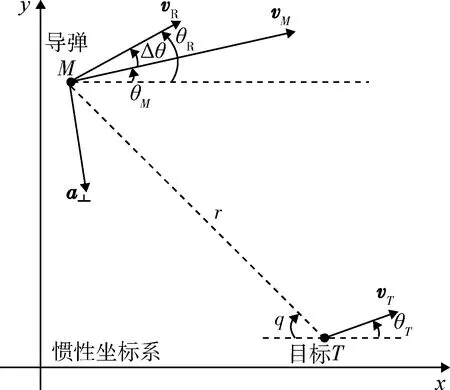
图1 弹目相对运动几何关系Fig.1 Relative motion geometry between missiles and targets
根据弹目相对运动关系有
vR=vM-vT,
(1)
在x向和y向投影分别有
vRcosθR=vMcosθM-vTcosθT,
(2)
vRsinθR=vMsinθM-vTsinθT.
(3)
假设vT速度恒定,且实际情况下反坦克导弹速度vM远大于vT,因而θT的改变可认为对导引律的影响忽略不计,将式(2)和(3)进行微分处理后有
(4)
(5)
(4)×cosθR+(5)×sinθR得到
(6)
(4)×sinθR-(5)×cosθR得到
(7)
另外弹目相对运动微分方程有
(8)
(9)
用Γ表示导弹落角,有Γ=θM-θT,如图2所示。根据弹目碰撞三角形关系有
(10)
由正弦定理可以得到
Δθ=arcsin(sin ΔvT/vR).
(11)
进而得出导弹落角Γ与θR关系有
θR=θT+Γ+Δθ.
(12)

图2 弹目碰撞三角形图Fig.2 Collision triangle diagram between missiles and targets
2 偏置比例导引律的设计
弹目相对运动形式的导引律为
(13)
式中:k为比例导引系数;b为偏置项。
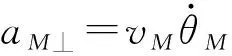
(14)

(15)
对式(13)两边积分有
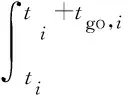
(16)
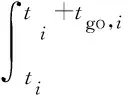
Bi=kqi+(1-k)θR,f-θR,i.
(17)
相应地对式(12)在终端tf时刻有Δθf=arcsin(sinΓ·vT/vR,f)即
θR,f=θT+Γ+Δθf.
(18)
代入式(17)有
Bi=kqi+(1-k)(θT+Γ+Δθf)-θR,i.
(19)
对于剩余飞行时间可以作近似估计
(20)
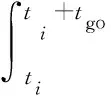
(21)
可以近似得到
(22)
3 仿真分析
3.1 不同导引律对比分析
为便于对比分析此导引律性能,选取弹道成型制导律[9]、两段变增益比例导引律[11]进行仿真分析对比,两者的形式如下:
(23)
(24)
式中:λ由文献[11]给出:
(25)
同时,为研究导引律的能量需求,引入控制能量消耗
(26)
仿真基本参数如下:导弹初始位置M(0,200),速度vM=300 m/s,目标初始位置T(2 500,0),速度vT=20 m/s。此偏置比例导引律的比例系数选取k=3,设置三者期望落角均为Δ=-60°,θM0=30°,θT0=30°。利用Matlab/Simulink软件,设置当弹目距离r<0.1 m时计算停止。
仿真结果如表1和图3所示。仿真图表中以BPNG表示落角约束的偏置比例导引律,KPNG表示两段变增益比例导引律,OPNG表示弹道成型导引律。
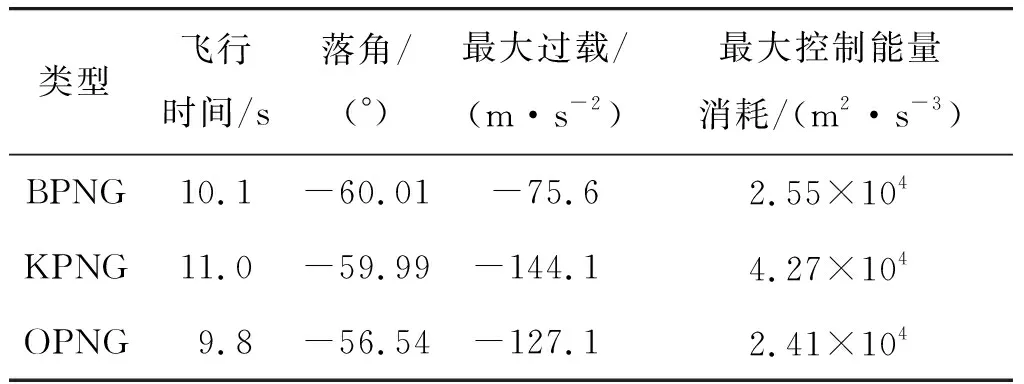
表1 不同导引律对同一目标计算结果(Δ=-60°)Table 1 Different guidance laws calculation results for the same target (Δ=-60°)
通过表1可以看出,BPNG与OPNG飞行时间接近,较KPNG约有1 s差异;对导弹最终落角进行比较,BPNG与KPNG对导弹落角控制精度较好,OPNG与期望落角误差偏大;另外BPNG最大过载远小于KPNG和OPNG,结合图3b)可以看出KPNG过载有跳变现象,最大值出现在制导指令切换时刻;全过程累积控制能量消耗BPNG与OPNG接近,且小于KPNG。
从图3a)的弹道曲线可以发现,3种导引律均通过调高初始攻击段弹道弧度来实现增大导弹落角的目的,在满足落角约束的前提下KPNG弹道爬升幅度最大,BPNG和OPNG弹道收敛更快;对3种导引律法向过载分析如图3b)所示,BPNG的法向过载变化范围最小,OPNG命中时刻的过载最大,而KPNG过载变化中有明显的跳变,此时制导指令改变,法向过载最大值出现在此时刻,此后过载逐渐减小;分析三者导弹倾角变化如图3c),倾角均由初始倾角30°逐渐减小到预设期望落角值,BPNG和OPNG曲线变化相似,而KPNG曲线分2段,前期缓慢减小,制导指令切换后以较快速度改变至期望落角值;对三者控制能量消耗曲线对比分析如图3d),BPNG和OPNG曲线平缓增加,而KPNG在制导指令切换后急速增大。
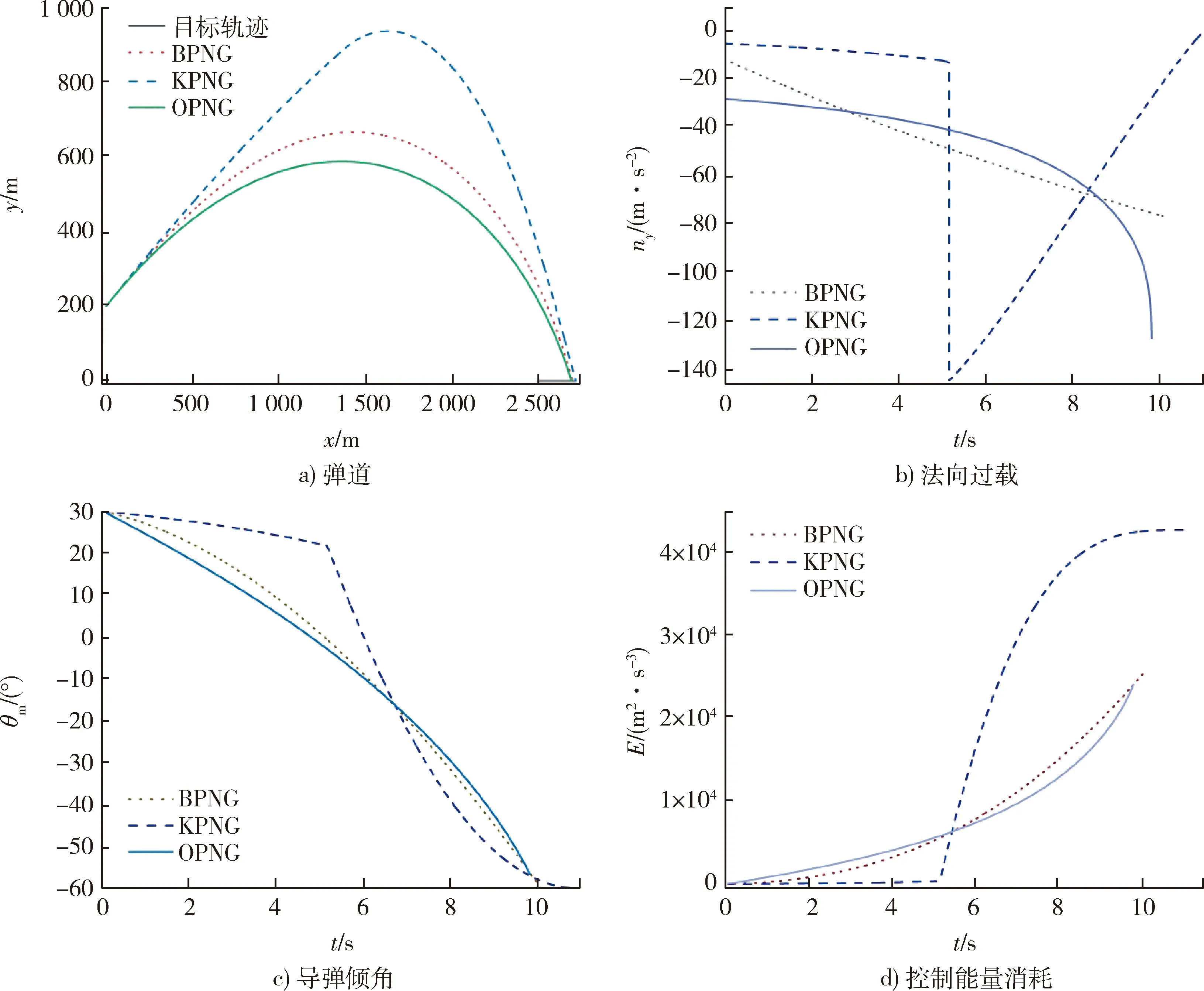
图3 落角约束Δ=-60°下3种制导律下对比图Fig.3 Comparison of three guidance laws under impact angle constraint for Δ=-60°
综合进行考虑,KPNG和BPNG落角精度较高,但KPNG弹道高度较大,且比例系数转换后导致过载有跳变,进而引起控制能量消耗的急速增大,对导弹载荷设计以及燃料携带有更高的要求;对于导弹末端过载和落角误差,OPNG相对BPNG偏大,可见BPNG的制导性能相对较好。
3.2 偏置比例导引律性能研究
为充分分析BPNG的制导性能,给定不同初始条件进行仿真分析,结果如表2所示。可以看出,此制导律有较高的制导精度。如图4所示,随着期望落角约束的增大,导致弹道的初始爬升高度会增大,以获取更大的终端落角。结合图5和图6不难看出,导弹过载和控制能量消耗有较大改变。可见,落角约束并不是越大越好,根据目标类型的不同可以选取不同的落角约束。如坦克等重装甲目标可以适当增大落角约束,如步兵车等轻装甲车等可以适当减小落角约束。
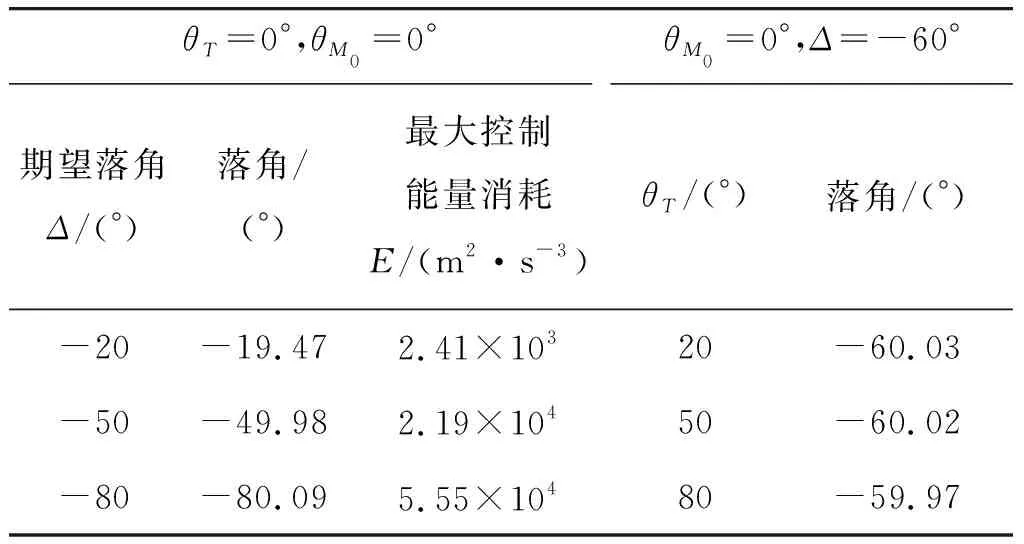
表2 不同初始条件下的仿真结果Table 2 Simulation results under different initial conditions
为探讨此导引律在飞行过程中制导指令的切换,图7给出了不同落角约束下的偏置项和弹目视线角速率随时间变化曲线。从中可以看出,此偏置比例导引律初始导弹爬升阶段主要起到制导指令作用的为偏置项b,之后随着b的逐步减小,弹目角速率逐渐增大,比例项对制导指令起到主导作用。落角约束越大,需要的偏置项b也随之增大,弹目角速率改变也更快。结合图4可以看出,该制导方案能够保证导弹在末制导前期利用偏置项b进行弹道爬升,中后期利用比例项来完成落角约束时也保证弹道的收敛。

图4 不同落角约束下的弹道曲线Fig.4 Ballistic curve under different impact angle constraints

图5 不同落角约束下的法向过载曲线Fig.5 Normal overload curve under different impact angle constraints

图6 不同落角约束下的控制能量消耗曲线Fig.6 Control energy consumption curve under different impact angle constraints
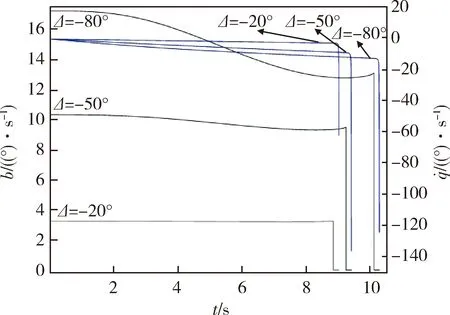
图7 不同落角约束下的偏置项和 弹目视线角速率变化曲线Fig.7 Bais and line-of-sight angular rate curve under different impact angle constraints
4 结束语
精确控制反坦克导弹的终端落角,对于目标毁伤具有重要的意义。本文通过弹目碰撞三角形关系,探究了弹目相对速度与落角约束之间的关系,进而给出了基于落角约束的变增益偏置比例导引律的关系式。通过与弹道成型制导律和分段变增益比例导引律对比,此导引律具有较高的制导精度,同时过载变化和控制能量消耗均较小。另外,计算表明,此制导律可满足不同仿真条件并具有较高的精度,但随着落角约束增大,导弹过载和控制能量消耗变化相应加剧,表明落角约束不是越大越好。最后进一步探讨此导引律的各项系数对弹道的影响,对偏置项和弹目视线角速率变化分析表明,初始阶段偏置项起到制导指令主导作用,弹道爬升,后续比例项对制导指令起主要作用,完成落角约束同时也保证了弹道的收敛。
本文的制导方案在满足落角约束的同时无需精确计算剩余飞行时间,提高了导引律的实用价值,可为直升机机载反坦克导弹制导律的设计提供参考。

