喷锡钢网曲线偏置方法研究
罗 铭,李 贵,3
(1 武汉科技大学 冶金装备及其控制教育部重点实验室,武汉 430081;2 武汉科技大学机械传动与制造过程湖北省重点实验室,武汉 430081;3 武汉科技大学 精密制造研究院,武汉 430081)
0 引 言
随着通信技术的发展,合路器在通信系统中应用越来越广泛,如大型商场、地铁的信号覆盖等。应用最多的是同轴腔体合路器,主要装载在腔体排腔结构中,主体结构包括腔体、与腔体相对拼装为一体的盖板以及装设于腔体上的公共端口。合路器腔体结构如图1所示。加工腔体过程中,需要借助喷锡钢网对腔体表层喷锡。喷锡钢网的平面结构是通过基曲线经过多次偏置而来的,一般是由人工借助CAD软件偏置功能与剪切功能实现,有大量重复且容易出错的操作,设计效率低下。在基曲线偏置的过程中,偏置曲线很容易与其他结构发生干涉,对于该问题的处理,迄今为止还无法用软件加以实现。

图1 合路器腔体Fig.1 Combiner cavity
对于曲线偏置问题,很多学者都进行了大量研究。Lee等人采用基曲线与二次贝塞尔曲线段的卷积来计算偏置曲线,可以有效避免偏置曲线自相交。Seong等人通过求解偏置曲线二次多项式方程的零集,并借助数字步进方法提高了消除自相交的精度。朱洪军等人通过检测偏置点的位置有效性对自相交点域进行消除。黄常标等人基于轮廓线方程来求解偏置曲线,并通过轮廓线方向向量来消除干涉问题。万健等人提出了一种基于区间算术和四叉树的算法来解决曲线自相交问题。朱虎等人根据挤压工具运动轨迹,提出了基于Sterolithography模型的顶点偏置算法以及多边形边偏置算法。查光成等人将加工件表面离散为Sterolithography模型,可以成功提取得到三角点坐标,进而通过偏置完成支撑体模型设计。朱亮等人提出了一种软干涉检查方法,利用分割思想将实体包围盒空间划分成若干体积相同的空间格。洪庆飞等人等人通过对自相交程度分析估量,采用一种有效的正则化方法来避免产生自相交的矢量图轮廓。李斌等人提出了一种基于轴角的干涉判断方法,并基于人工势场法对机器人进行路径规划。
上述研究并未考虑到异体结构在曲线偏置过程中的影响。本文通过分析喷锡钢网曲线偏置案例,针对偏置过程出现的一系列问题,基于图论以及曲线重构思想,提出一种复合多段线偏置算法,成功解决了复合多段线偏置过程效率低、且存在自相交的问题,并对偏置后孤岛体的绕行问题进行了自动化处理,提高了典型喷锡钢网结构设计的质量与效率。
1 喷锡钢网平面结构分析
喷锡钢网二维平面结构如图2所示。图2(a)是孤岛体与基曲线组成的喷锡钢网基础构造体。经过一系列曲线偏置过程,连通路以及处于连通路内的孤岛体共同组成了典型的喷锡钢网结构,见图2(b)。

图2 喷锡钢网二维平面结构Fig.2 Two-dimensional plane structure of tin-sprayed steel mesh
基曲线是由多个直线段与曲线片段组成的复合多段线,线段间由节点联接,且节点处左、右两侧一阶导相同。基曲线具有严格的方向定义,满足右手定则。孤岛体是连通域的一种,其边界长度不超过10 mm,结构多样,可分为圆形孤岛体和异形孤岛体两大类。其中,圆形孤岛体为具有半径与圆心的圆,异形孤岛体则没有规定和限制,如图3所示。

图3 孤岛分类Fig.3 Island classification
2 基于曲线偏置的孤岛绕行算法
2.1 曲线偏置方法
喷锡钢网边界由复合多段线组成,复合多段线是多个直线与曲线片段的组合体。采用常规方法对复合多段线进行偏置,首先需要对复合多段线进行离散;依据偏置方向与偏置距离,对离散点进行偏置;最后,通过曲线拟合技术对偏置点进行曲线拟合。但这种方法迭代次数高,效率低,曲线拟合后的边界实体与实际复合多段线偏置实体还存在一定误差。因此,本文提出了一种新的复合多段线偏置方法,详细过程如下:
(1)提取复合多段线的每一个节点信息。节点是子线段间的联接点,节点信息包括点坐标、凸度值和法线向量,其中凸度值控制着2点之间曲线弧度大小和方向,确定2点坐标和对应的凸度值即可唯一确定一段弧线。凸度值定义如图4所示,凸度值被定义为1/4的圆心角正切值,通过凸度即可计算圆心角、半径和圆心坐标等信息。

图4 凸度值定义Fig.4 Bulge value definition
对于任意节点,当该节点凸度为0时,意味着该节点与相邻的下一节点之间由直线连接;否则,2点之间由圆弧线段连接。依据节点信息,构建节点数据结构,如公式(1)所示:

其中,表示凸度值,为法线单位向量。
将节点集作为离散点集,可大大减少偏置时的迭代次数。
(2)遍历离散点集,以离散点中存储的法线方向向量为偏置方向,根据偏置距离偏置离散点,获取偏置点集。构建偏置点数据结构,偏置点信息与对应的离散点除坐标信息不同外,其他均相同。
(3)依据偏置点集构建偏置后的线段集。遍历偏置点集,对于其中任一偏置点O,如果O的凸度值为0,则连接O O,作为偏置后的直线段,加入线段集;如果O的凸度值非零,则依据凸度值计算得到该圆弧段半径,从而依据点O,O与凸度值唯一确定一段圆弧,加入线段集。
(4)依据线段集构建偏置后的复合多段线。
纵观进博会上的各国展台,国外“特产”能在中国市场立足,除了得益于我国对外开放政策外,自身优势也很重要,其在加工、包装设计、市场细分等方面,有不少做法值得我们借鉴。拿泰国烧烤椰为例,普通的椰青经过烘烤,去除了纤维部分,留下的完整部分可以保鲜6个月。此举并未涉及什么技术难题,却使产品实现了从普通水果店铺到超市精品零食货架的跨越。又如,大洋洲一款针对孕妇的奶粉,打出“愿你生子归来,依然少女身材”的广告,十分引人注目。
2.2 偏置曲线自相交的解决
偏置曲线自相交问题是典型的偏置问题。在曲率突变的区域极有可能出现自相交,如图5所示。对于这种现象,一般去除蓝色加粗部分的线段,保留其余部分。

图5 偏置曲线自相交Fig.5 Bias curve self-intersection
为了实现喷锡钢网偏置需求,本文提出了一种解决复合多段线自相交问题的解决方法,具体过程如下:
(1)遍历线段集,对于任意线段R,分别求取R与其余线段的交点,并加入交点集。
(2)对于点集中任意一点,如果为偏置点集中的点,且点为相邻线段所得交点,则删除该点。遍历焦点集,删除所有满足上述条件的点,剩余点即为自相交点。
(3)依据偏置后的复合多段线方向与自相交点信息可以构建有向图{(),()},以图5(a)中偏置曲线自相交点为节点构建有向图如图6所示。图6中,顶点集(){,,,},由复合多段线的首尾两点与自相交点集构成,边集(){,,,}代表顶点集中2节点间的连接线段。
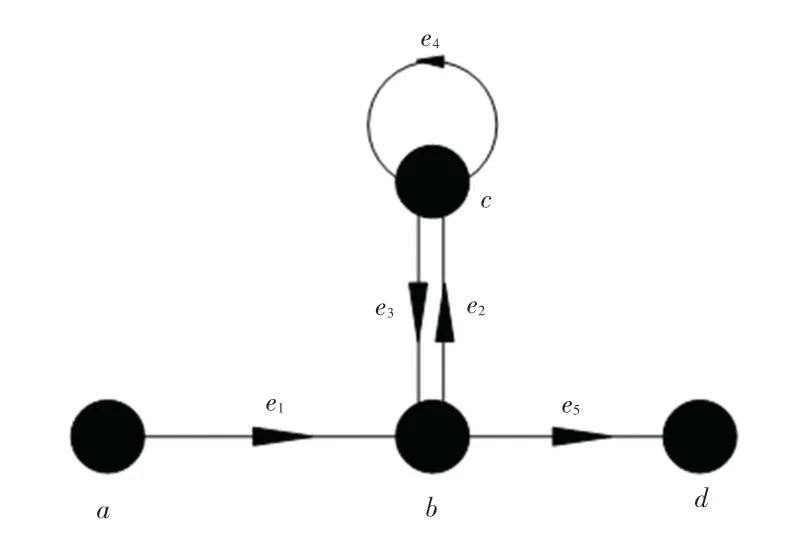
图6 有向图模型Fig.6 Directed graph model
(4)环是顶点数与边数相等的图,从图6中可以看出,有向图中存在2个环分别是,,,和,,用消除有向图中环的方法来简化偏置曲线自相交问题。剔除2个环中的边,,,形成了2个连通分支,2个连通分支的顶点集分别为{,,}和{}。剔除这一连通分支后,有向图为无重边和环的简单图,如图7所示。

图7 简单有向图Fig.7 Simple directed graph
(5)依据有向图理论简化了自相交消除过程,由于删除的是任意多段线片段,极有可能产生尖角。
2.3 孤岛绕行方法
对复合多段线偏置后,可能会出现孤岛结构与偏置曲线存在干涉的情况。对此拟展开研究分述如下。
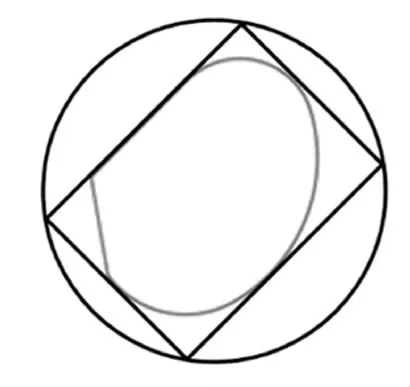
图8 孤岛结构简化Fig.8 Simplified island structure
求取孤岛外接圆与偏置多段线的交点。由喷锡钢网结构可知,交点至多不超过2个。如果交点个数为2个,则表示孤岛与偏置曲线存在干涉情况。
(2)对孤岛实体包络矩形外接圆进行偏置,偏置距离取外接圆到基曲线的最短距离。由于基曲线为复合多段线,获取复合多段线函数表达式是十分困难的。因此可以节选出孤岛附近的线段,分别计算附近线段与孤岛圆的距离,得到孤岛圆与基曲线的最短距离。计算线段与孤岛圆距离的数学公式见如下:
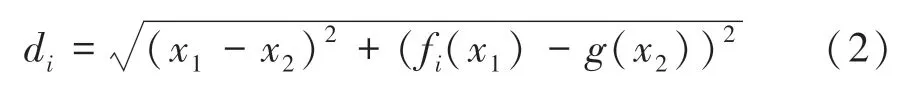
其中,为线段上一点的横坐标;f()为对应的纵坐标值;为孤岛外接圆上一点的横坐标;g()为对应的纵坐标值。
(3)偏置孤岛外接圆后,去除掉偏置圆内的偏置曲线段和偏置方向上的偏置圆片段,偏置曲线孤岛绕行如图9所示。由图9可以看出,剪切后原本平滑的线段出现了多处尖角,不符合喷锡钢网复合多段线的连续性要求,因此,需要进一步对偏置曲线进行处理,消除尖角。

图9 偏置曲线孤岛绕行Fig.9 Offset curve island detour
这里,研究给出了消除尖角的过程,详述如下:
(1)合并剪切后的偏置曲线与尖角部分,组成重构后的偏置曲线。并对偏置曲线按照等弧长离散,得到离散点集{,,,…,p}。
(2)遍历离散点集,计算任意相邻两点切向向量夹角,依据公式(3)对偏置点集进行筛选:
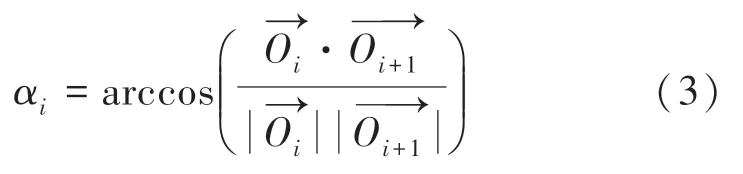
当任意离散点所对应的切向向量夹角α大于角度阈值时,则需要删除点P与P,继续计算P和P对应的切向转角,否则,继续检测α。
(3)将筛选后的离散点集作为样本点,重新构建偏置曲线。依据此方法将转角过大的部分消除,解决对偏置曲线尖角问题。尖角消除过程如图10所示。

图10 尖角消除Fig.10 Elimination of sharp corners
3 实例讨论
通过实例从曲线偏置质量和效率两个方面来验证本偏置算法的性能。现有待偏置的复合多段线,长度为307.99 mm,节点数为4个,其中直线段数量为1,曲线段数量为2,偏置距离20 mm,圆形孤岛与异形孤岛各一个。
首先对复合多段线进行偏置,并对孤岛体定位,如图11所示。
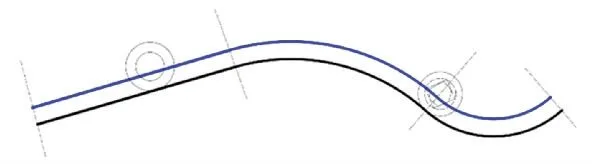
图11 复合多段线偏置与孤岛定位Fig.11 Compound polyline offset and island location
然后,依据曲线重构思想,对偏置曲线和孤岛外接圆进行重组,形成新的绕岛偏置曲线,如图12所示。
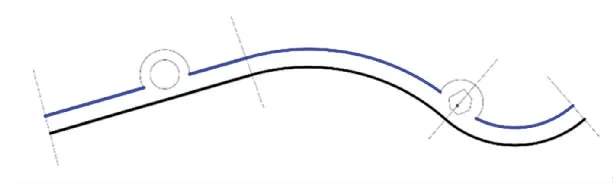
图12 偏置曲线几何重构Fig.12 Geometric reconstruction of the bias curve
最后,依据离散点切向矢量进行尖角处理,使得偏置曲线更为平顺美观,尖角处理与曲线拟合如图13所示。
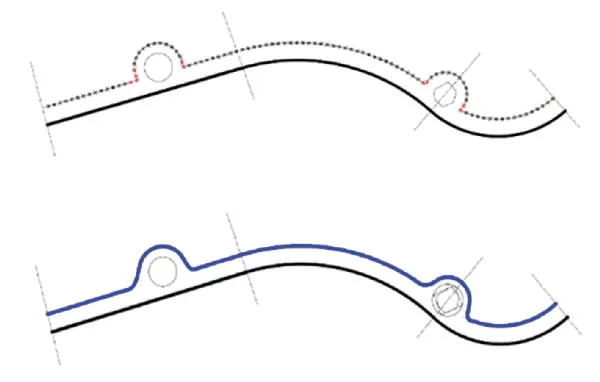
图13 尖角处理与曲线拟合Fig.13 Sharp corners processing and curve fitting
偏置曲线没有自相交和偏置尖角,同时在孤岛体处也能很好地进行绕行,偏置曲线的过渡较为自然,没有扭曲。综上所述,本文算法能够得到较为理想的孤岛绕行的偏置曲线,可应用于喷锡钢网曲线偏置的实际设计。
4 结束语
总结了喷锡钢网设计过程中的难点与问题。同时,对喷锡钢网的平面几何结构进行了分析与解释。针对偏置曲线效率低的问题,提出了复合多段线偏置方法,并依据有向图思想,解决了偏置曲线的自相交问题;针对偏置曲线与孤岛干涉问题,提出了偏置曲线孤岛绕行方法,并基于切向矢量角度计算方法,消除了偏置曲线的尖角问题;最后,通过将算法应用于实例,所得到的偏置曲线无尖角与自相交点,且与孤岛结构无干涉情况,完全满足偏置要求。采用本方法对喷锡钢网进行结构设计,能够大大减少人工操作时间与工作量,是辅助喷锡钢网设计的一个有效的工具。

