星模拟器光学系统视场拼接方法的研究

付景怡，秦天翔，黄蕴涵，刘智颖

（长春理工大学 光电工程学院，吉林 长春 130022）

1 引言

星模拟器是重要的地面标定设备[1]，可在地面模拟星体的排布、姿态，标定并检测星敏感器的探测能力[2-3]。近年来，星模拟器要求视场更大、精度更高[4-7]。为了增大视场，获得更广的视野范围，陈启梦等人通过拼接硅基液晶显示器件(Liquid Crystal on Silicon, LCoS)显示器件的方式，解决了大视场下星图显示器件分辨率不足的问题，将准直系统的视场增大到22°[8]；刘欢等人提出了一种算法，能够很好地校正畸变，减少了像差对视场的约束，并且采用特殊的光学材料来优化光学系统，使光学系统的视场达到20°[9]；代雨等人利用二次成像方法，设计了一款双光组结合的投影系统，并使用DMD芯片作为星图显示器件，使视场达到28.6°[10-11]。

单一星模拟器受到自身像质和显示芯片大小的限制，继续增大视场的实现度和性价比都很低，而且光学系统的设计会变得异常复杂与困难。

本文提出一种通过拼接视场增大星模拟器视场的方法。为了在增大视场的同时降低重量、简化组合方式、降低成本，本文根据平面几何关系得到不同拼接方式，计算并分析了各方式下的视场利用率，利用编程软件计算了每个单一视场中心坐标和相邻视场交点坐标，进而确定了所需的精准拼接数目。对比视场利用率与拼接数目，得到了最佳拼接方式，实现了视场的增大。

2 视场拼接原理

在视场拼接中，用一个圆锥体来模拟单一小视场的范围，张角的中心轴模拟小视场光学系统的光轴，圆锥体的顶角就是光学系统视场的张角。相同的视场要用相同大小的圆锥体表示；视场大小不同，圆锥体的底面积大小则不同。将处在不同角度、相同大小的小圆锥体拼接起来，可以近似形成更大的圆锥体。通过这样的原理将在不同方位的单一小视场拼接起来，从而形成更大的视场[12]。如图1所示，ω 为单一视场角，W为拼接后形成的视场角。

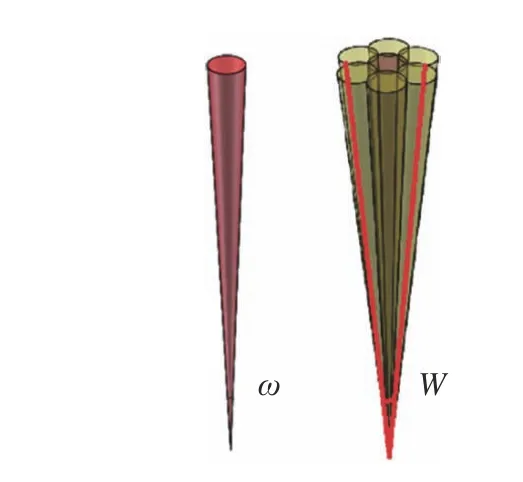
图1 拼接前后视场角对比图Fig.1 Contrast of the FOV angle before and after splicing

能否实现视场完全拼接，则取决于单一视场间的轴间夹角 θA，即两个小圆锥轴线的夹角(见图2)。当轴间夹角小于圆锥锥角时，相邻的两个单一小视场范围之间有重叠，才能保证视场信息不丢失。若轴间夹角大于视场角，则两个单一小视场之间会出现间隙，从而导致得到的视场不连续。拼接完成后，显示部分将通过算法处理重叠问题，利用算法对每个单一星模拟器的星图进行修剪，剪裁掉多余的重复像素，再拼接成一个完整的星图。

图2 圆锥轴间夹角示意图Fig.2 Schematic diagram of the angle between shafts

3 平面拼接简化模型

针对小视场系统难以继续扩大视场的局限性，为了简化大视场模型并实现无缝拼接，提出了一种基于平面的拼接方式。以单一的小视场为主体，当单一视场投影圆的内接正多边形能够无缝衔接起来时，就可以使各个小圆无空隙地拼接在一个面上，从而完成无缝拼接。以平面为模型的无缝拼接的前提是若平面产生微小弧度变化，相邻两单一视场间仍能保证没有空隙；而若平面拼接时有重叠部分，则拼接后的视场角度越大，重叠比例就越大。并且，这种拼接方式在拼接过程中对轴间夹角角度无特殊要求，适用于视场为任何大小的光学系统拼接。

若想使内接正多边形在平面上无缝拼接，则要满足以下条件：

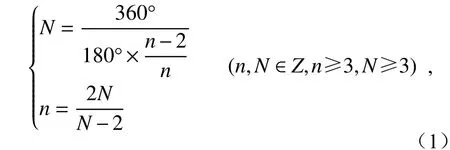
其中，n为 正多边形的边数，N为使用的多边形个数。

计算得到n分别为3，4，6。也就是说，在平面上只有相同的正三角形、正四边形或正六边形能够不重叠地无缝拼接成一个平面，如图3所示。

图3 无缝拼接示意图Fig.3 Schematic diagram of three types of seamless splicings

由此得到3种视场拼接方式，分别为正三角形、正四边形和正六边形拼接，示意图如图4所示。

图4 3种拼接方式拼接效果Fig.4 Splicing effects of three splicing methods

平面简化模型是为了更直观地获得视场拼接后的效果。但在实际应用中，各单一星模拟器分布在一个球面上。因此要通过后期算法实现平面向三维立体结构的转化。通过单一视场间的轴间夹角 θA能够确定相邻星模拟器之间的固有关系，从而对图像进行剪切和拼接，使图像映射在球面上[13]。

4 视场利用率的计算方法

相邻的单一小视场之间要有一定的重叠部分，这样可以避免视场信息丢失，重叠区域大小直接影响可利用的视场大小。因此借鉴填充率概念[14]提出了视场利用率的概念。视场利用率是指除去重叠部分，拼接后大视场覆盖的范围和拼接过程中使用的所有单一小视场覆盖范围的比值。根据各拼接方式下的几何关系，能够近似确定重叠部分。视场利用率为ηn的计算方式为：

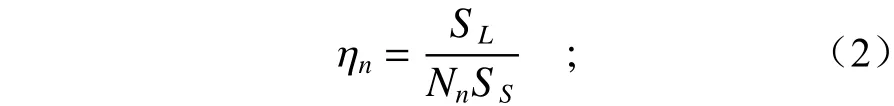
重叠部分所占比例kn为

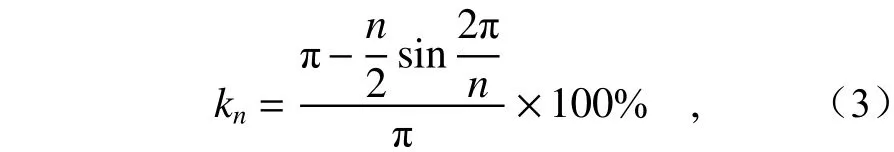
其中，Nn为正n边 形拼接方式下所需的n边形个数；SL为 拼接后大视场覆盖面积；SS为单一小视场覆盖面积。

根据平面几何关系，得到视场利用率与重叠部分的关系为

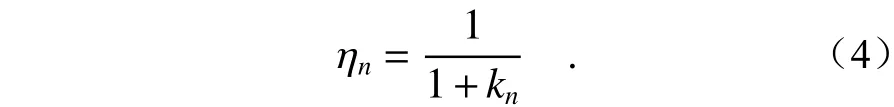
5 拼接数目的计算模型

5.1 轴间夹角计算

轴间夹角是两个单一小视场中心轴线的夹角，也可以说是单一视场之间的夹角。前文提到，当轴间夹角小于单一视场角时，相邻的两个单一小视场之间才会发生重叠，保证视场信息不丢失。通过单一小视场的轴间夹角能够计算出各个小视场的准确位置，进而精准地确定拼接数目，因此轴间夹角的数值在拼接过程中具有重要作用。3种拼接方式的轴间夹角如图5所示。

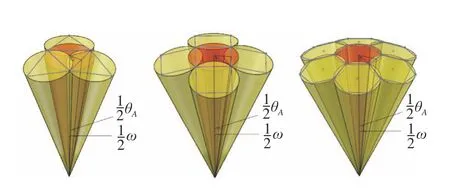
图5 3种拼接方式的轴间夹角Fig.5 The angle between the axes of the three splicing methods

图5展示出轴间夹角大小和单一小视场之间存在一定的几何关系，得到以下关系式：

其中θAn为 正n边形拼接的轴间夹角。

5.2 拼接数目计算

在平面拼接中，3种方式拼接后大视场的投影图如图6所示，可以明显看到3种方式都是以环形阵列的方式向外排布，最终形成的视场形状也不是圆形，而是正多边形，因此利用该模型求出的解只能大致计算出每种方式的拼接数目。图6中展示了3种拼接方式下拼接两圈之后各自与圆形视场投影的关系。

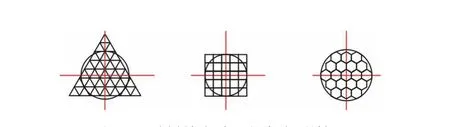
图6 3种拼接方式下视场投影情况Fig.6 Field of view projection results in three splicing modes

5.2.1 拼接圈数C

对于拼接后大视场投影形成的圆形来说，拼接的圈数位置定义在圆形的直径位置，而对于拼接后形成的正多边形视场来说，拼接圈数位置是正多边形的穿过重心平行底边的直线位置，因此要在拼接过程中使两个位置统一。除正三角形拼接方式以外的其他两种方式单一视场的圆心都在同一直线上，而正三角形拼接方式不同，因此正三角形拼接方式要进行单独计算。定义除中心视场外，向外排布的第一环为第一圈，以此类推，如图7所示。

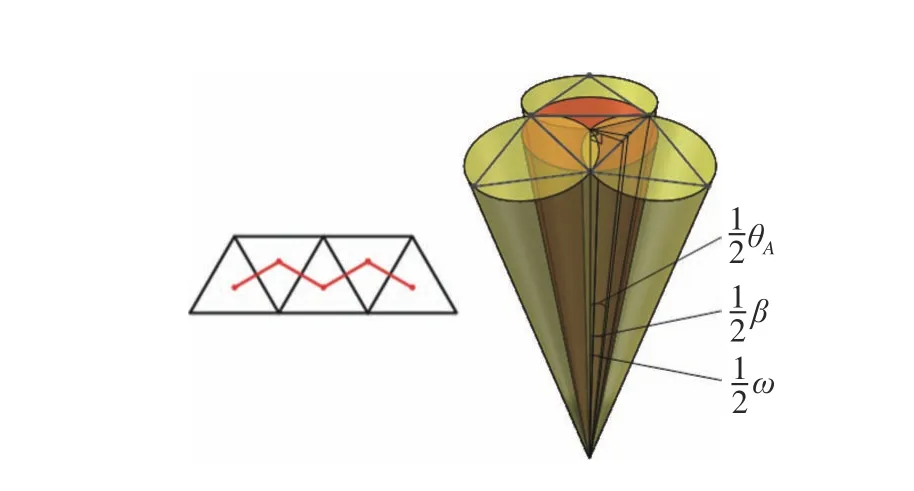
图7 正三角形拼接方式夹角计算示意图Fig.7 Schematic diagram of the calculation of the included angle of the regular triangle splicing method

正四边形拼接圈数与正六边形拼接圈数C的计算方式相同，即：

取整，其中n= 4或6。

对于正三角形拼接法，设在水平方向相邻两圈的夹角为β，则有

则得到三角形拼接圈数C3为

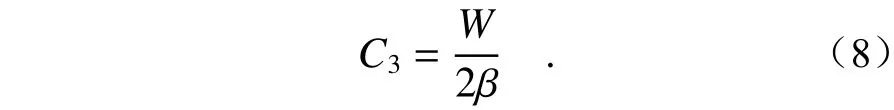
5.2.2 拼接数目Sn

在计算了3种拼接方式的圈数后，就要对整体拼接数目进行求解，由图4可以看出每种方式的排布都是有规律的，找到每一圈排布个数的规律就能确定整体的排布个数。以6圈为例，就足以推导出3种方式的拼接数目。

5.2.2.1 正三角形拼接方式

对于正三角形拼接方式，其每一圈的个数如表1所示。

表1 正三角形拼接方式的圈数与个数关系Tab.1 Relationship between the number of circles and the number of regular triangle splicing method

由表1能够推导出每一圈的个数公式为

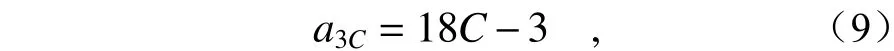
则得到三角形拼接方式所需拼接数目为

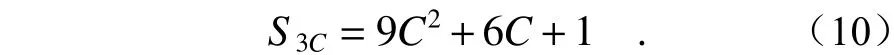
5.2.2.2 正四边形拼接方式

正四边形拼接方式，其每一圈的个数如表2所示。

表2 正四边形拼接方式的圈数与个数关系Tab.2 Relationship between the number of circles and the number of square splicing method

由表2推导出每一圈的个数公式为

得到正四边形拼接方式所需拼接数目为

5.2.2.3 正六边形拼接方式

正六边形拼接方式，是以6的倍数向外排列，其每一圈的个数如表3所示。

表3 正六边形拼接方式的圈数与个数关系Tab.3 Relationship between the number of circles and the number of regular hexagon splicing method

由表3推导出每一圈的个数公式为

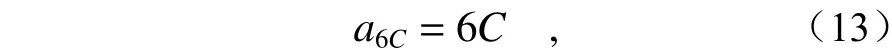
最终推导出正六边形拼接方式所需的拼接数目为

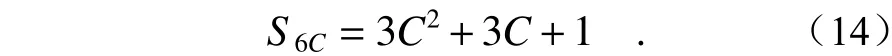
以上能够得到3种拼接方式大致的拼接数目，但是由于拼接的实质是圆形小视场的内接正多边形无缝衔接，因此拼接过程中肯定会有视场部分缺失或冗余的情况，由图6也可以看出。要解决这个问题则需要计算每个视场所在的准确位置。

6 拼接数目的计算与分析

在大致了解各拼接方式需要的单一小视场数目之后，就要对单一小视场进行更精准的定位和详细计算，以确定各个方式所需要的准确拼接数目，从而决定采用哪种拼接方式。确定坐标时，选择将所有的坐标做归一化处理，以保证坐标位置只和单一视场角的大小有关。以正六边形拼接方式为例，建立坐标系如图8(彩图见期刊电子版)所示。

图8 坐标系的建立Fig.8 Establishment of the coordinate system

计算坐标时，要找到各点间能够成立的几何关系。而不同位置的求解方法不同，需要求解的点分为3类：内部单一小视场中心坐标、对角线位置单一小视场中心坐标和相邻小视场交点坐标。

内部单一视场的中心坐标如图9中O1−1、O1−2、O1−3、O1−4、O1−5、O1−6所示，这6个位 置与O的夹角都相等，均为轴间夹角，放到图9下点O1−1与 点A1、A2的角度和直线距离都相等，得到式（15），并据此得到其坐标位置。坐标边界位置计算示意图如图10所示。

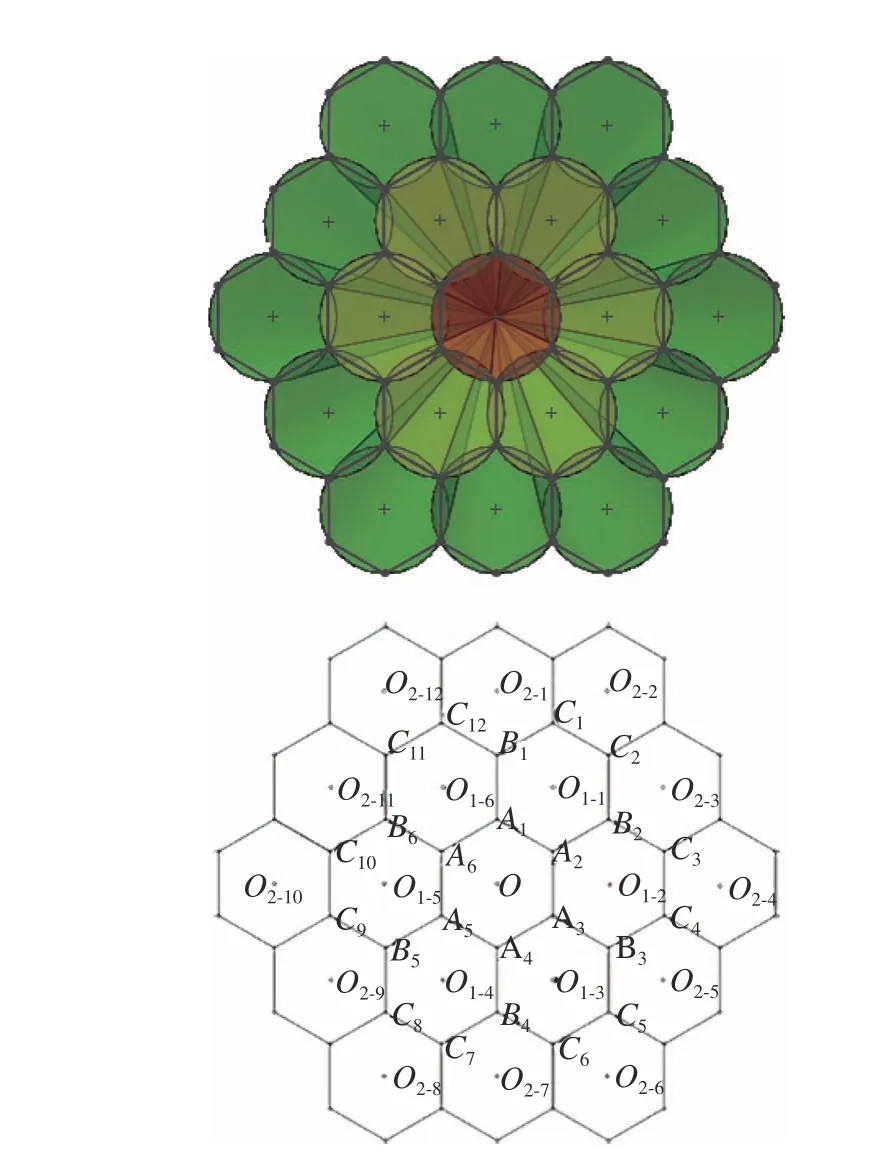
图9 中心坐标与交点坐标位置排列Fig.9 Arrangement of the center coordinates and intersection coordinates

图10 坐标边界位置计算示意图Fig.10 Schematic diagram of calculation of the coordinate boundary position

对于相邻单一视场之间的交点坐标B、C等，根据B1与O1−1、O1−6的夹角都是单一小视场的半视场角，有如下等式：

对 角 线 位 置 单 一 视 场中 心 坐 标O2−2、O2−4、O2−6、O2−8、O2−10、O2−12等，O2−2与O1−1的夹角为轴间夹角，其到点O2−1、 点O2−3的直线距离相同，得到式(17)。而O2−1、O2−3皆可由式(15)求得。

根据式(17)，利用编程软件编写程序可得到每个单一视场中心坐标与交点坐标。

根据式(5)能够计算出各个方式下的轴间夹角大小，在编程软件中即可以得到每个单一视场中心坐标与交点坐标位置。为了确定精准的拼接数目，需计算出拼接到所需大视场的边界坐标位置，也就是最外圈所在的坐标位置，将边界坐标点与编程软件中得出的坐标点进行对比，在该边界坐标点以外的点都不在需求范围内。由于坐标是环状分布，则无法给定x、y轴的边界位置，但z轴方向的高度边界位置可求，即

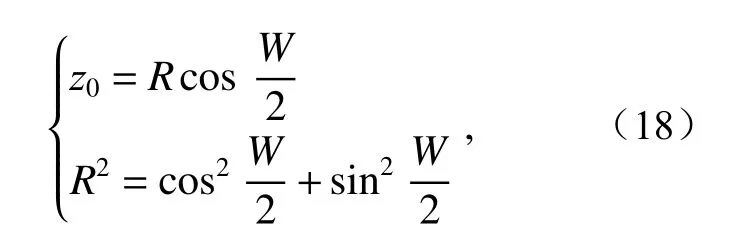
其中，z0为边界位置的坐标高度。

7 3种拼接方式对比分析

针对以上3种拼接方式，为了对他们的视场利用率以及相同视场所需要的单一小视场数目分别进行讨论，以 ω=5°的单一视场向外拼接成为W=90°、W=120°、W=150°、W=180°为例，对3种方式进行对比分析。

7.1 视场利用率对比

根据式(2)～式(4)可知，视场利用率只与单一小视场内接正多边形的边数有关，即与拼接方式有关，因此3种拼接方式下的视场利用率为定值。而根据式(5)，各拼接方式下的轴间夹角的大小与单一小视场的视场角有关，当给定单一小视场为 ω=5°时，则可计算3种方式下的轴间夹角，分别将n= 3、4、6与ω =5°代入相应公式。得到结果 如表4所示。

表4 3种方式的视场利用率对比Tab.4 Comparison of FOV utilization of three methods

对比结果显示：正六边形拼接方式的视场利用率是3种方式中最大的，重复部分最少。

7.2 拼接数目对比

由式(6)～式(14)能够得到，拼接数目与单一小视场角和拼接后的大视场角都有关，拼接成不同的大视场，所需的精确拼接数目会有所变化，因此要讨论拼接成不同大视场的情况并做对比。用编程软件计算由 ω=5°的单一小视场拼接成W=90°、W=120°、W=150°、W=180°情况下的拼接数目，见表5。

表5 3种方式的拼接数目对比Tab.5 Comparison of the number of splices for three methods

由图11可以看出：正三角形拼接的增长率很大，拼接的视场越大，增加的拼接数目越多；而正四边形与正六边形拼接变化相对平缓，并且无论拼接为任何数值的大视场，正六边形拼接的拼接数目始终最少。

图11 3种方式的拼接数目趋势图Fig.11 Trends in the number of splices in three ways

8 结论

本文针对星模拟器光学系统视场难以增大的问题，提出了对星模拟器单一小视场进行拼接的方法，以此达到增大视场的目的。以平面拼接模型为基础，得到有效的拼接方式，为正三角形、正四边形与正六边形3种，并计算了各种方式的视场利用率。利用编程软件确定3种拼接方式的单一小视场坐标位置，从而得到3种方式下的拼接数目。结果表明，正六边形拼接方式的视场利用率最高，可达到三角形拼接方式的1.4倍，并且其拼接数目最少，可以减少系统重量、降低成本。本次研究结果不仅可以应用在星模拟器准直光学系统视场增大中，还可以应用于其他光学系统的视场增大，对今后光学设计中模拟大视场具有一定意义。