耦合电感型Boost-Sepic 高增益DC-DC 变换器

郭 瑞，张力之，韩 冬，黄陈辉

（辽宁工程技术大学电气与控制工程学院，葫芦岛 125105）

在空间飞行器中，直流母线电压需要满足蓄电池充电和各种负载工作的需要，同时要考虑线路损耗等因素，因此直流母线电压较高，通常取100 V，此时需用DC-DC 变换器来解决这一问题[1]。

传统变换器难以满足实际电压增益，DC-DC变换器实现高增益的办法主要有4 种：①变换器级联法[2-5]，该方法具有变换器器件多、可靠性低等缺点；②串联变换器输出法[6，7]，由于并联结构要求输出电压纹波相同，导致各子变换器的输出电容增加；③开关电容电感法[8-11]，该方法无法实现任意电压输出，而且在开关电容电感串并联切换时会出现较大尖峰电流；④耦合电感法[12-15]，该方法可通过设定耦合电感绕组匝数比来实现任意电压输出，而且具有变换器元件少、可靠性高等优点，所以广受关注。

针对提高DC-DC 变换器的电压增益问题，可采用耦合电感的方法来实现高增益。文献[16，17]提出了在传统Boost 变换器中引入耦合电感单元法，吸收了漏感，增加了增益，实现了零电压关断和开通；文献[18]提出了耦合电感型高增益DC-DC 变换器，引入耦合电感和倍压电路、钳位电路，增加了电压增益且减小了开关应力。

基于以上研究，本文变换器把传统Boost-Sepic电路中的电感换成耦合电感一次侧，耦合电感二次侧则和两个倍压单元结合变成桥式倍压单元加入传统Boost-Sepic 电路中，以此增加变换器的增益并降低开关管的电压应力。

1 工作原理

本文提出的耦合电感型Boost-Sepic 高增益DC-DC 变换器电路如图1 所示。可看出，传统Boost变换器和传统Sepic 变换器共用输入端，再将Sepic变换器的输出端叠加在传统Boost 变换器输出端；然后采用耦合电感使增益更高，结构更灵活；在耦合电感一次侧加入钳位电容吸收耦合电感漏感能量，损耗更小，效率更高；在耦合电感二次侧加入桥式倍压单元可解决谐振和开关管电压尖峰较大问题，故在Boost-Sepic 变换器基础上，耦合电感一次侧代替Sepic 中电感，耦合电感二次侧代替新加的桥式倍压单元中的电感。针对开关管零电压问题，本文在开关管S 两端并联二极管和电容。图1 中，Vi为输入电源，L1为输入电感，S 为开关管，C0～C5为电容，Lm为励磁电感，Lk为漏感，Np为耦合电感的原边，NS为耦合电感的副边，耦合电感的匝比n=NS/Np，V0为输出电压，R0为负载。假设：所有器件为理想器件；所有电容足够大，其两端电压恒定。

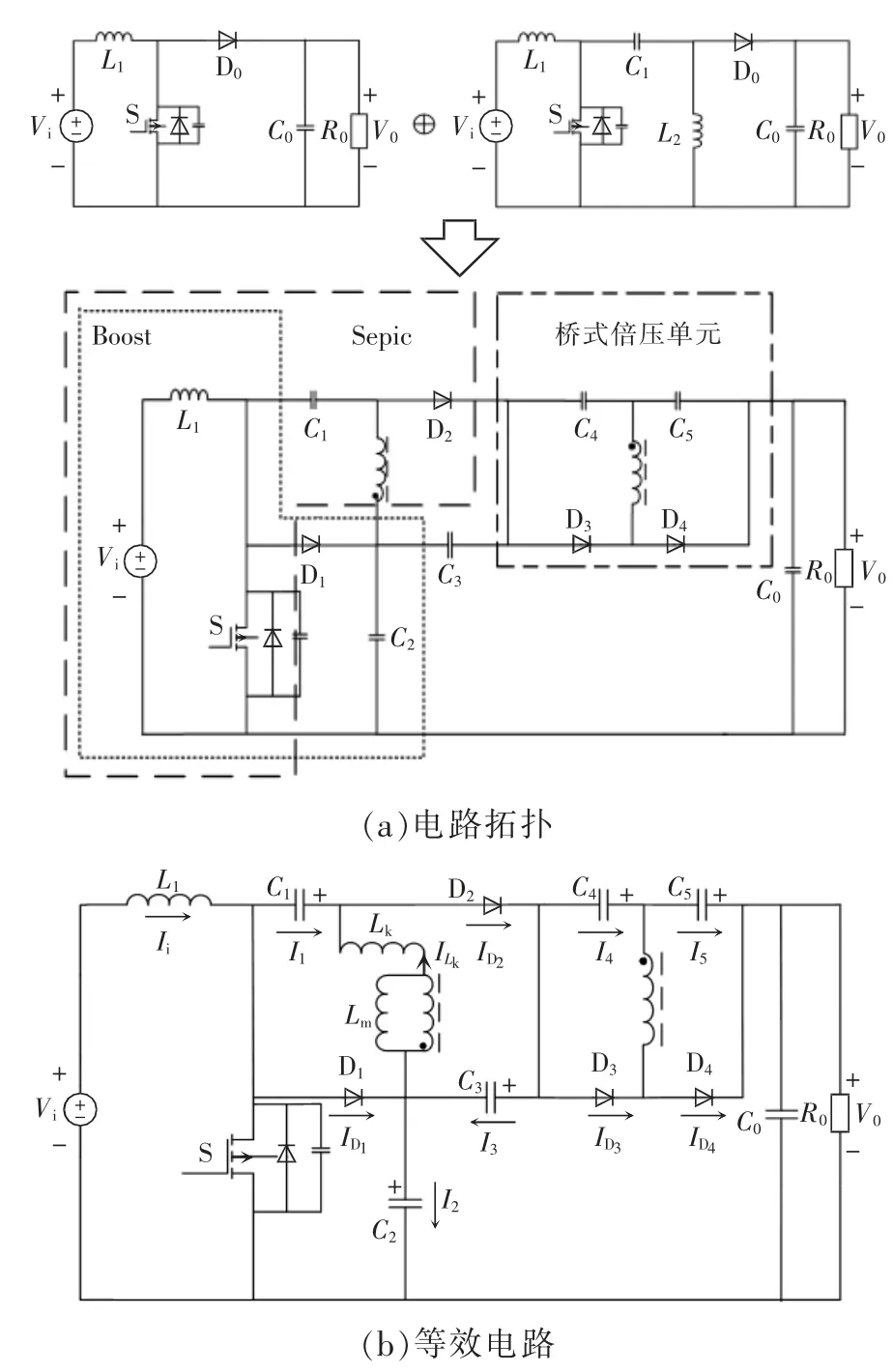
图1 耦合电感型Boost-Sepic 高增益DC-DC 变换器Fig.1 Boost-Sepic high-gain DC-DC converter with coupled inductors

变换器稳态工作时，一个开关周期的主要工作波形如图2 所示。变换器在一个周期内可分为7 个开关模态，每种开关模态等效电路如图3 所示。

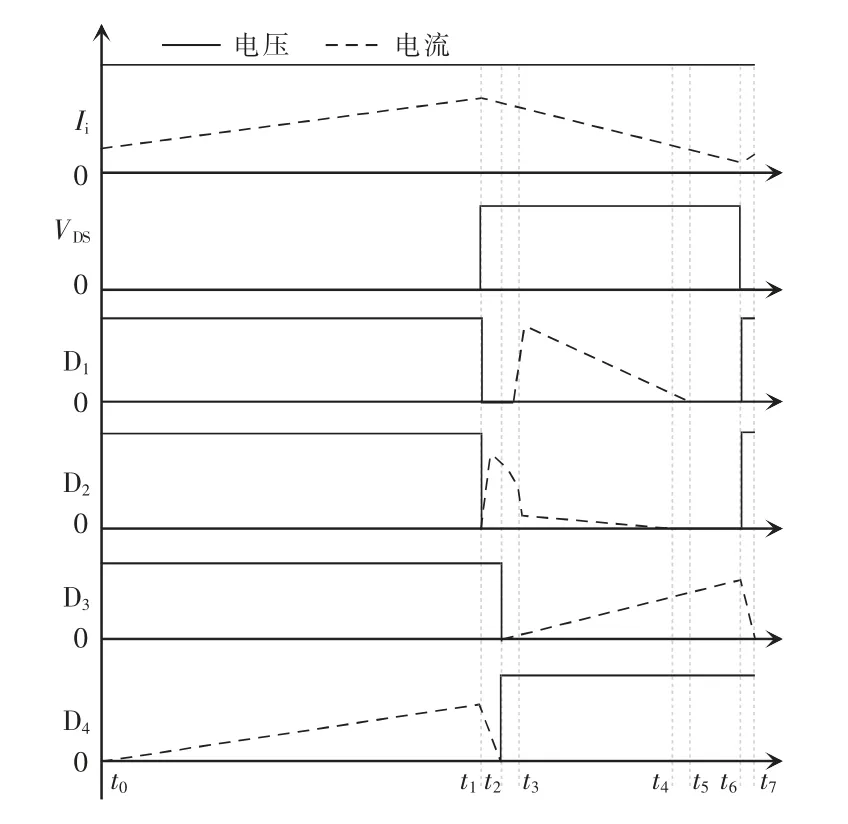
图2 变换器的主要工作波形Fig.2 Main working waveforms of converter

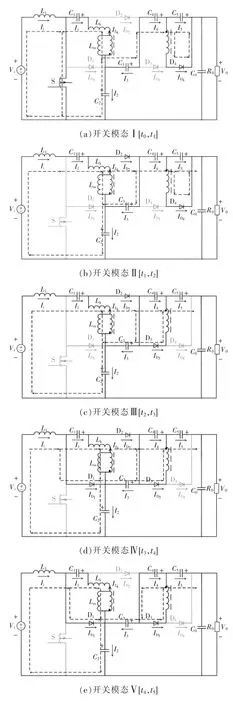
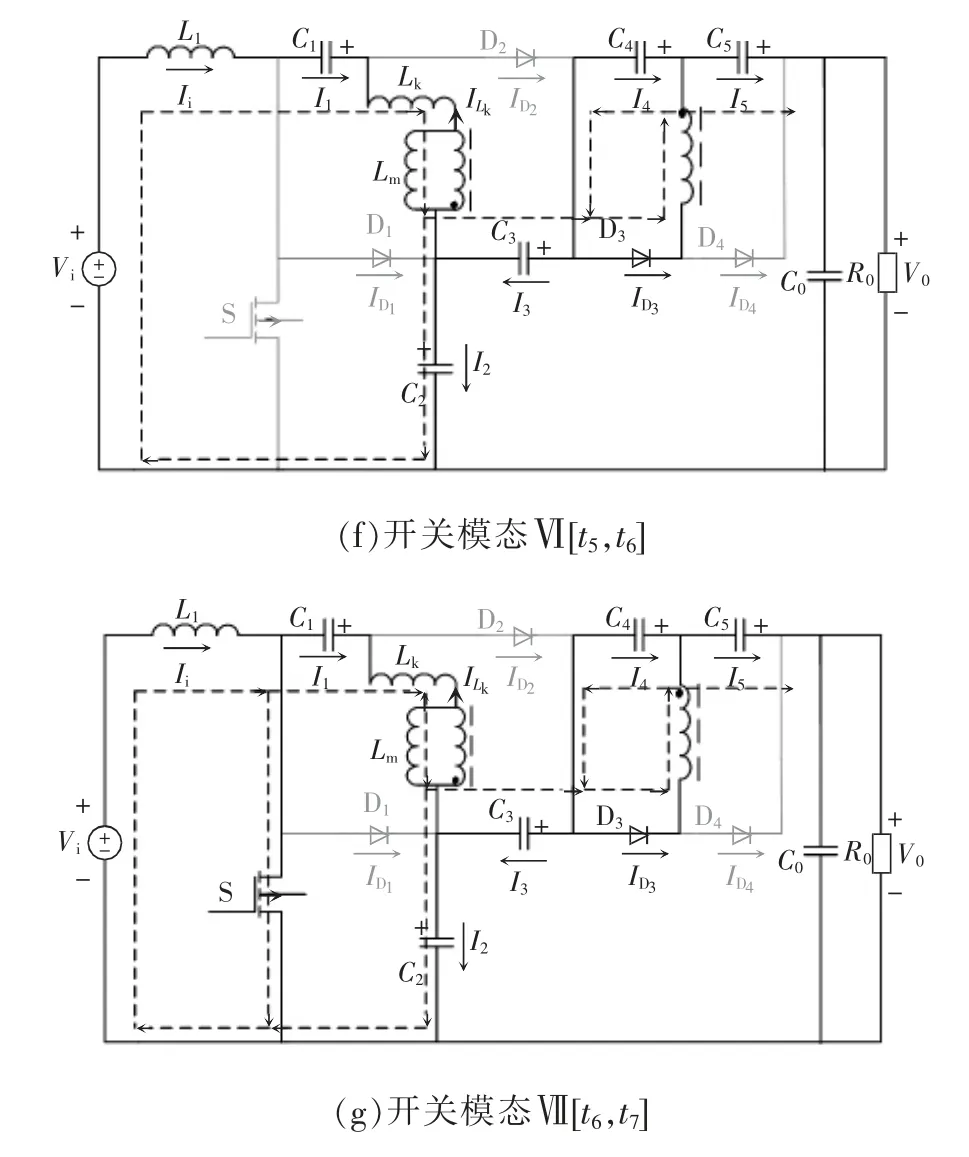
图3 各开关模态的等效电路Fig.3 Equivalent circuit in each switching mode

（1）开关模态Ⅰ[t0，t1]：该模态中，开关管S 导通，二极管D4导通，二极管D1、D2和D3关断；电源与输入电感L1构成回路，故电源给输入电感L1提供能量，电流iL1近似线性上升；电容C1、C2和耦合电感一次侧构成回路，故电容C2、C1给耦合电感一次侧提供能量，励磁电感储能；经检测输出电流I0为0，故电容C3、C4、C5和耦合电感二次侧构成回路，电容C3、C4为电容C5和耦合电感二次侧充电。其中，电感L1的电压和励磁电感电压的表达式为

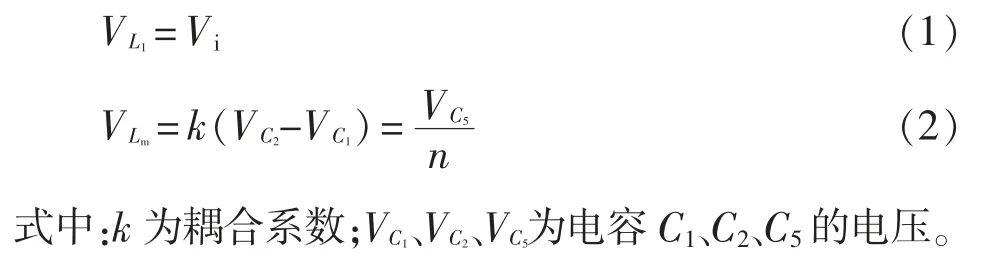
（2）开关模态Ⅱ[t1，t2]：S 关断，D2、D4导通，D1、D3关断；左侧电源、L1、C1、C2与耦合电感一次侧构成回路，故电源、L1及C1为C2和耦合电感一次侧提供能量，电流iL1近似线性减小；耦合电感一次侧的两端电压被二极管D2钳位在电容C3电压-VC3，故二极管D2的电流iD2快速上升；经检测输出电流I0开始线性上升，故耦合电感二次侧给C5和负载提供能量。其中，励磁电感电压的表达式为

（3）开关模态Ⅲ[t2，t3]：S 关断，D2、D3导通，D1、D4关断；t2时刻D4承受反向电压使流经D4的电流为0；左侧电源、L1、C1、C2与耦合电感一次侧构成回路，耦合电感一次侧与C3并联，故电源、L1及C1为C2、C3和耦合电感一次侧提供能量，电流近似线性减小；输出电流I0为正，C4、C5能量向负载转移。其中，L1的电压和励磁电感电压的表达式为

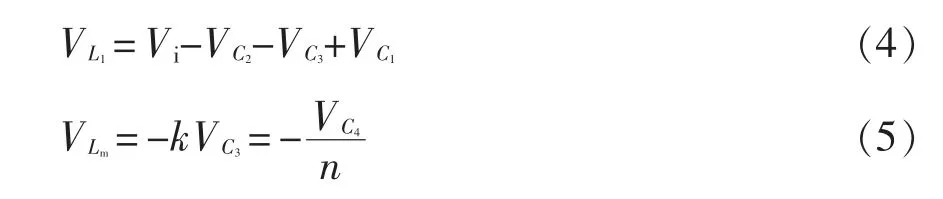
（4）开关模态Ⅳ[t3，t4]：S 关断，D1、D2和D3导通，D4关断；t3时刻流经D2的电流急剧下降，D1导通；左侧电源、L1与C2与耦合电感一次侧构成回路，故C2储能；由于D1导通，耦合电感一次侧电流方向改变，耦合电感漏感电流则反向近似线性上升，其中C1、C3释放能量，C2吸收能量；右侧C4、C5一起为负载提供能量；其中，L1的电压和励磁电感电压的表达式为

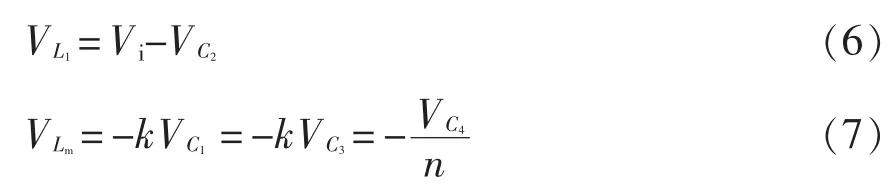
（5）开关模态Ⅴ[t4，t5]：S 关断，D1、D3导通，D2和D4关断；t4时刻流经D2的电流下降为0，左侧电源、输入L1与C2与耦合电感一次侧构成回路，故C2储能，电流则反向近似线性上升；耦合电感一次侧的两端电压被D1钳位在-，故D1的电流快速上升；C4、C5一起为负载提供能量，耦合电感的二次侧电流ifu近似线性下降。

（6）开关模态Ⅵ[t5，t6]：S 关断，D3导通，D1、D2和D4关断；t5时刻流经D1的电流为0，左侧电源、输入L1、C1、C2与耦合电感一次侧构成回路，电源和储存在电感L1中的能量为C1和C2和耦合电感一次侧提供能量，电流则反向近似线性上升，L1的电流持续线性减小；C3、C5一起为负载提供能量，二次侧电流ifu近似线性下降。

（7）开关模态Ⅶ[t6，t7]：S 导通，D3导通，D1、D2和D4关断；电源与输入L1构成回路，电流持续近似线性增大；C1给C2和耦合电感一次侧构成回路，且在t6时刻时，流经D3的电流极具下降，故漏感电流则反向近似线性减小；C3、C5和耦合电感二次侧一起为负载提供能量，二次侧电流ifu反向近似线性减小。其中，励磁电感电压的表达式为

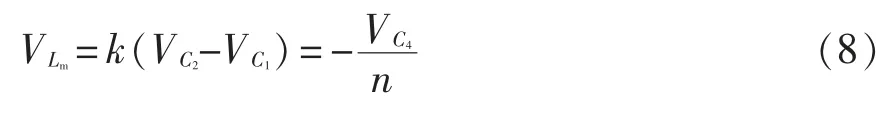
2 性能分析

2.1 电压增益

耦合电感的耦合系数k 为

由式（1）、式（6）和电感L1伏秒平衡定理可得

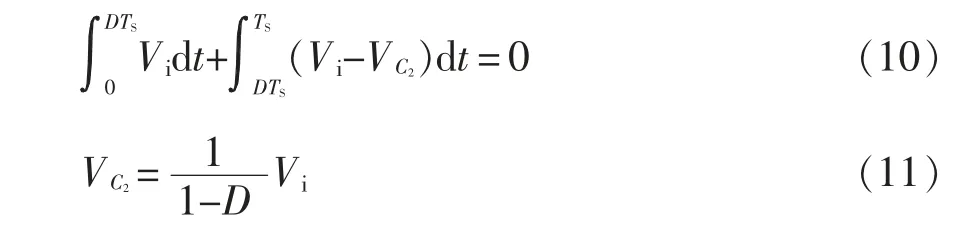
根据式（2）、式（7）和励磁电感Lm伏秒平衡定理可得

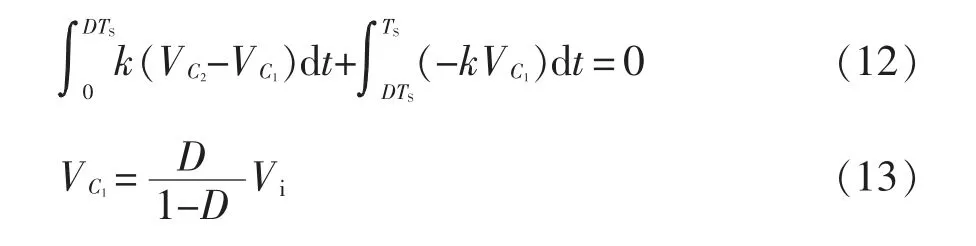
根据式（1）、式（4）和电感L1伏秒平衡定理可得

根据式（3）、式（5）和励磁电感Lm伏秒平衡定理可得

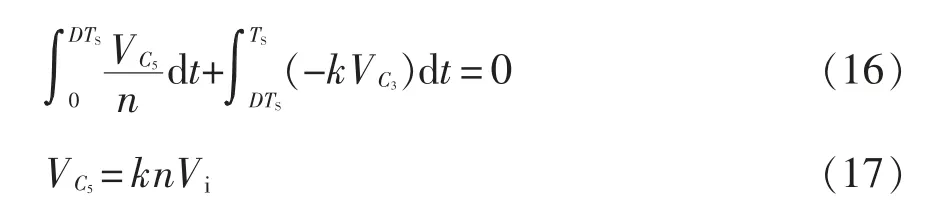
根据式（2）、式（5）和励磁电感Lm伏秒平衡定理可得

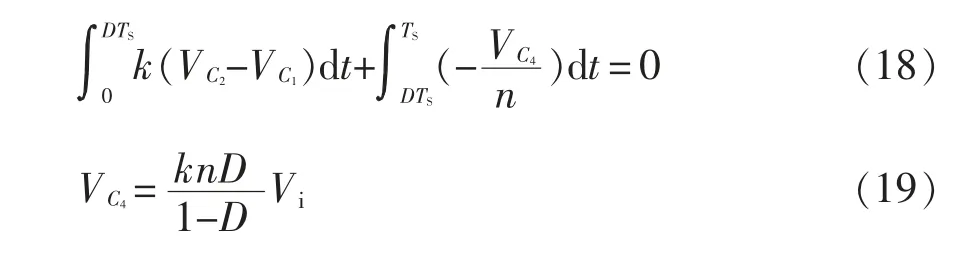
根据模态Ⅴ和式（11）、式（15）、式（17）、式（19）可得

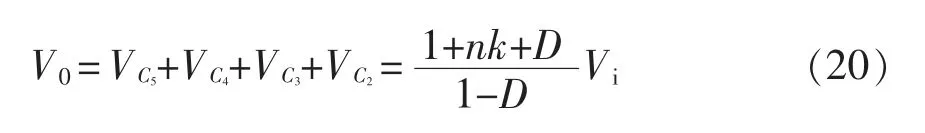
故本文变换器的电压增益GV为

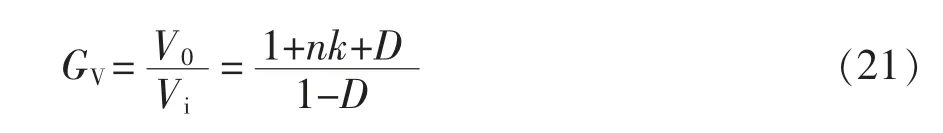
当k=1，该变换器的电压增益GV为

可看出，变换器电压增益GV取决于占空比D 及耦合电感的匝比n。

当k=1 且D=0.6，该变换器的电压增益GV为

可看出，电压增益GV和匝比n 成正比，实际中占空比D 的选择一般不超过0.7，因此可通过调节n 来提高GV，避免极限占空比的情况。

图4 为匝比n=2 时，本文提出的变换器的增益GV、耦合系数k 和占空比D 的关系，可见占空比一定时，耦合系数k 越大变换器的增益GV越高，所以耦合电感应尽量紧密以提高电压增益GV。

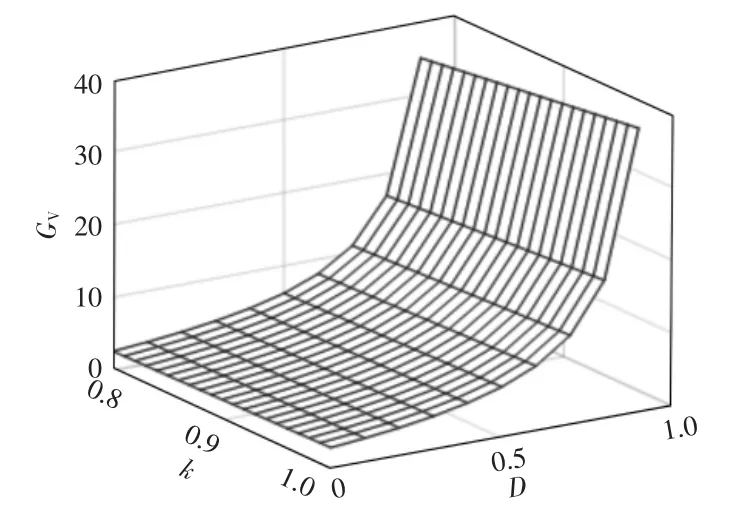
图4 变换器的电压增益、耦合系数和占空比的关系Fig.4 Relationship between the voltage gain of converter,coupling coefficient and duty cycle

2.2 电压应力

由图3（e）可得

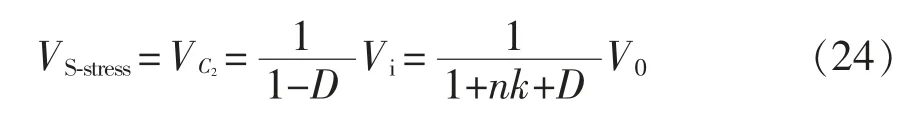
由图3（a）可得

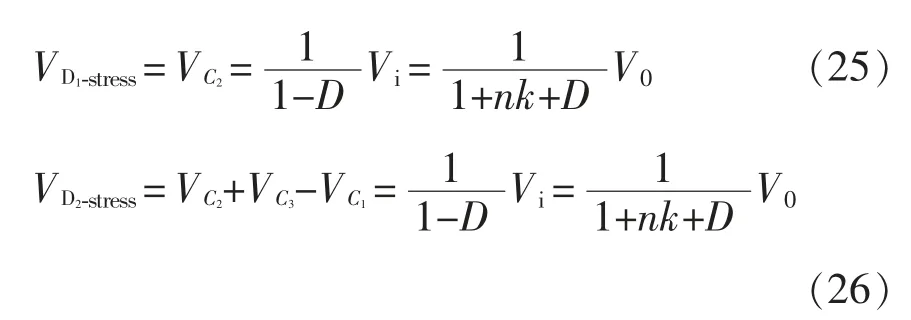
由图3（b）和图3（c）可得

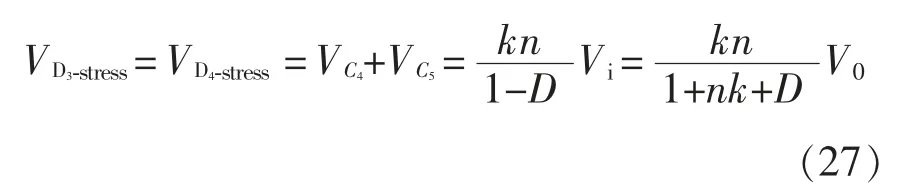
根据式（11）、式（13）、式（15）、式（17）、式（19）和式（20），电容C1～C5两端的电压分别为

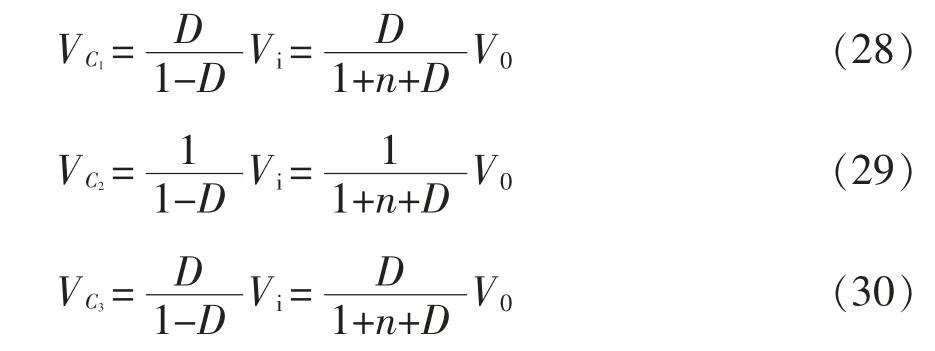
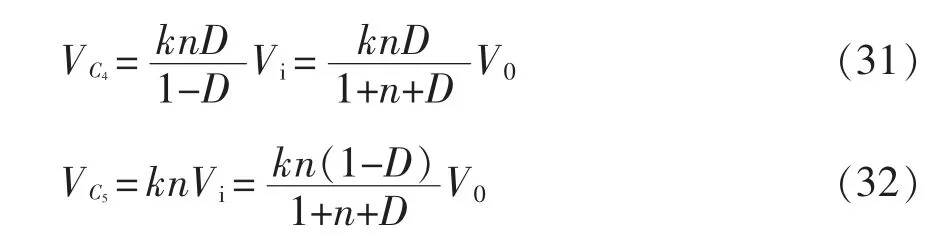
图5 是根据式（24）～式（27），D=0.6、k=1 且输入电压Vi=12 V 的情况下，变换器的开关管、二极管的电压应力与耦合电感匝比n 之间的关系。

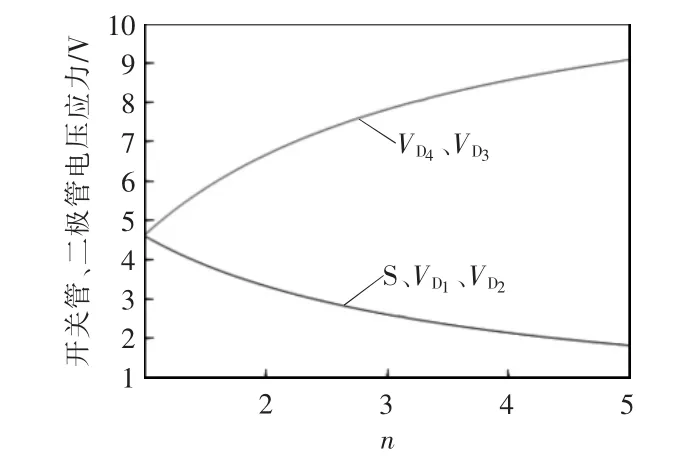
图5 功率器件的电压应力与匝比的关系Fig.5 Relationship between voltage stress in power devices and turns ratio n

根据图5 可以看出，随着匝比n 的增大，功率开关管S 和二极管D1、D2的电压应力与匝比n 成反比，二极管D3、D4的电压应力与匝比n 成正比，故设计耦合电感匝比时应考虑避免二极管D3、D4电压应力过高。

图6 是根据式（28）～式（32），其中D=0.6、k=1且输入电压Vi=12 V 的情况下，变换器电容的电压应力与耦合电感匝比n 之间的关系。由图6 可以看出，随着n 的增大，电容C1、C2、C3的电压应力与n成反比，电容C4、C5的电压应力与匝比n 成正比，故设计耦合电感匝比时应还要考虑避免电容C4、C5电压应力过高。

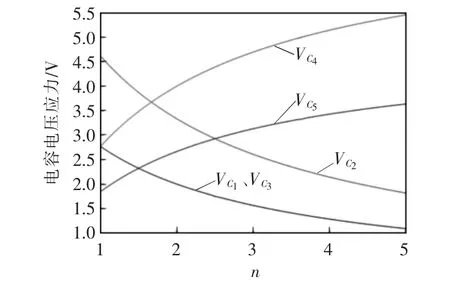
图6 电容C1～C5 电压应力与耦合电感匝比之间的关系Fig.6 Voltage stresses in C1～C5 versus turns ratio

根据式（23）知电压增益与匝比n 和占空比D的选取有关。应避免极限占空比，因此占空比D 取0.4～0.7。图5 和图6 表明：匝比n 的选取在1～4 合适。故占空比D=0.7 且匝比n=4 时，本文变换器的最高增益GV（max）=19。

3 性能对比

表1 为Sepic 变换器、文献[16]提出的变换器和本文提出的变换器的性能对比。可看出，相同输出的情况下，本文变换器对比Sepic 变换器、文献[16]所需的开关管和二极管的电压应力更低，低电压应力所需的开关管和二极管器件更便宜，节省了成本，DC-DC 变换器的损耗大部分来自开关器件，另外小部分损耗来自电感和电容，本文针对开关管的零电压问题在开关管S 两端并联二极管和电容，同时本文变换器缓解了二极管反向恢复问题，减小了损耗，提高了效率。

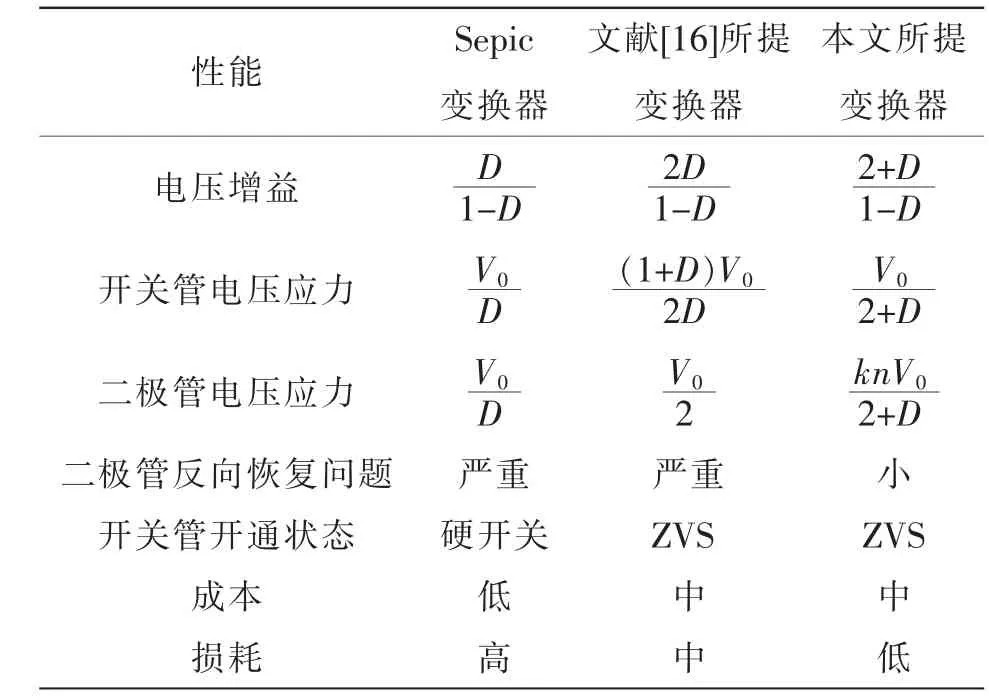
表1 不同变换器的性能对比Tab.1 Comparison of performance among different converters

图7 为Sepic 变换器、文献[16]提出的变换器和本文提出的变换器的开关管电压应力对比。根据图7 可以看出，虽然3 种变换器的开关管电压应力都与占空比D 成反比，但在占空比相同的情况下，本文提出的变换器开关管电压应力更低。

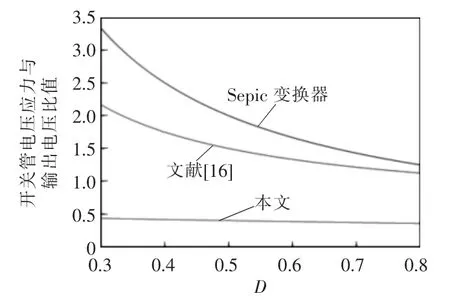
图7 不同变换器的开关管电压应力对比Fig.7 Comparison of voltage stress in switches among different converters

4 关键参数设计

本文变换器引入耦合电感来提高变换器的电压增益，故选择合适的耦合电感对变换器电压增益的提升有重要影响。电流纹波率r 是耦合电感设计中的重要参数，其值一般选为0.3～0.5，故本文设计中r 取0.4。

4.1 匝比

设计匝比时要考虑最小输入电压（Vi（min）=8）和最大占空比（Dmax=0.7），此时，耦合电感原边励磁电感峰值电流最大，根据电压增益式（22）可得

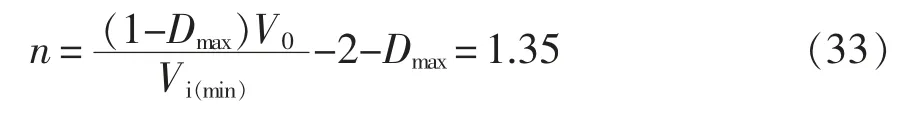
在第2.2 节对匝比的分析可知，对于耦合电感的匝比的选择时需要综合考虑，故选取耦合电感的匝比为n=2，此时最大占空比Dmax=0.655。

4.2 输入电感

对耦合电感型Boost-Sepic 高增益DC-DC 变换器的工作原理分析可知，当开关导通时，有

由式（34）得电感为

本文变换器的最大输出电流I0=W/V0=1.08 A，一般电感电流的纹波分量小于其直流分量的20%，即=0.2IL=1.08 A，可得在实际中要考虑一定裕量和手工绕制的误差，最终绕制所得电感L1接近150 μH。

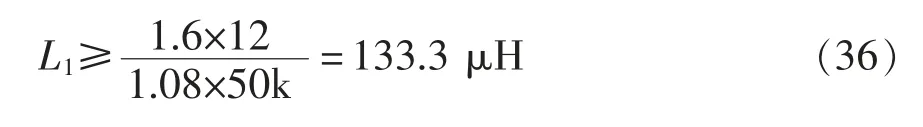
4.3 电容

电容电压应力控制在一定范围情况下，可根据电压纹波的要求选取电容。电容C1～C5取值为

式中：P0为输出功率；ΔVC分别为电容C1～C5的电压纹波；fS为开关频率。

5 实验验证

通过搭建一台耦合电感型Boost-Sepic 高增益DC-DC 变换器来验证理论分析的正确性，器件选择见表2，实验样机平台如图8 所示。

表2 变换器的器件选择Tab.2 Selection of converter components

图8 实验样机平台Fig.8 Platform of experimental prototype

图9～图16 为变换器的实验波形。图9 为输入电压Vi和输出电压V0波形，可看出本文变换器实现了较高的增益；图10 为驱动信号VGS、输入电感L1电流，可看出满足输入电流连续的特点；图11为耦合电感一次侧、二次侧电流波形；图12 为功率开关管S 的电压、电流波形，可看出开关应力VS-stress接近输出电压的1/4，并且开关管实现了零电压开通，减小了损耗；图13 和图14 为二极管D1～D4电流波形，可看出二极管能自然关断，缓解了反向恢复问题；图15 和图16 为二极管D1～D4电压波形，可看出二极管D1、D2电压应力约等于输出电压的1/4，二极管D3、D4的电压应力约为输出电压的1/2。实验结果验证了理论分析的正确性。

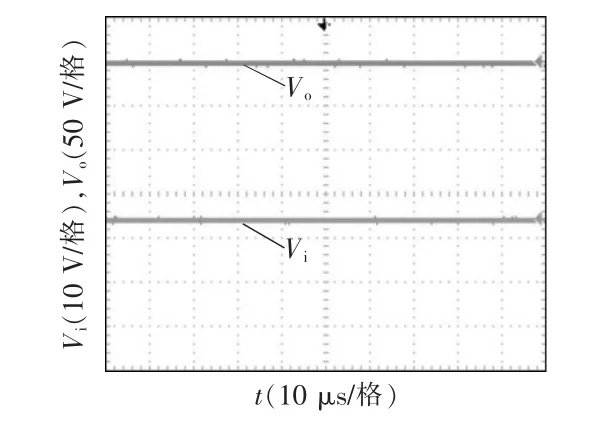
图9 输入电压Vi、输出电压V0 实验波形Fig.9 Experimental waveforms of Vi and V0

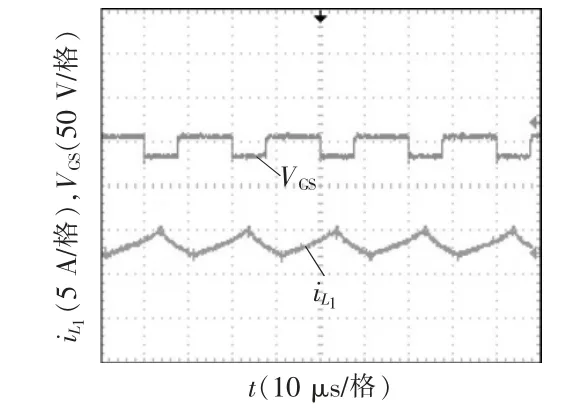
图10 驱动信号、输入电感L1 电流实验波形Fig.10 Experimental waveforms of VGS and

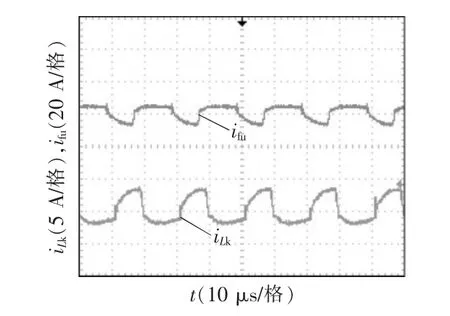
图11 耦合电感一次侧、二次侧电流实验波形Fig.11 Experimental waveforms of iLk and ifu

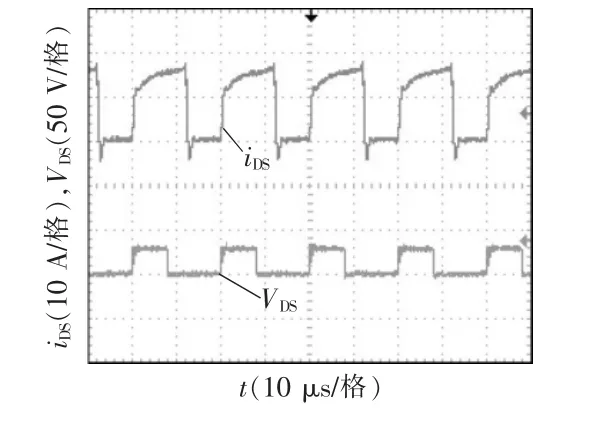
图12 开关管S 电流iDS 及电压VDS 实验波形Fig.12 Experimental waveforms of iDS and VDS

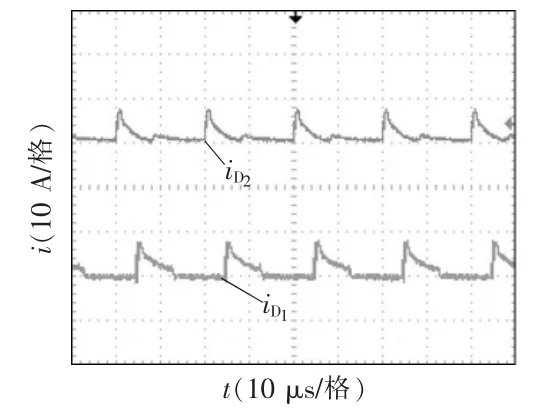
图13 二极管电流实验波形Fig.13 Experimental waveforms of and

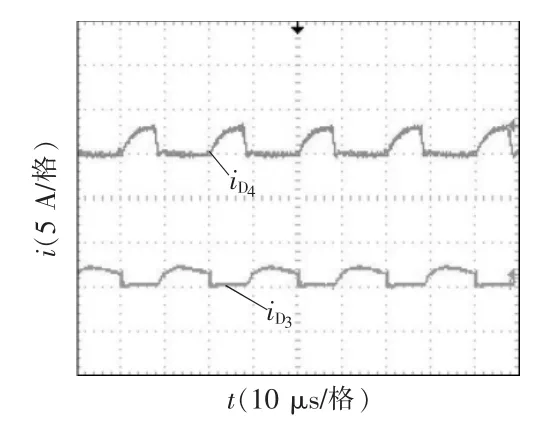
图14 二极管电流实验波形Fig.14 Experimental waveforms of and

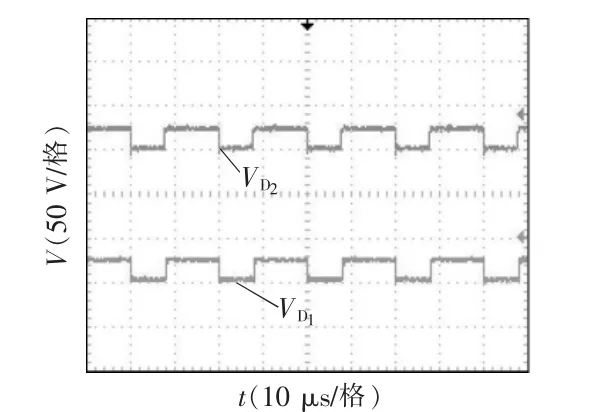
图15 二极管电压、实验波形Fig.15 Experimental waveforms of and

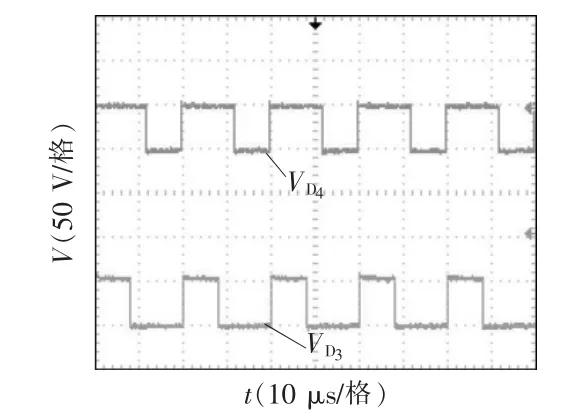
图16 二极管电压、实验波形Fig.16 Experimental waveforms of and

6 结论

本文提出一种耦合电感型Boost-Sepic 高增益DC-DC 变换器，通过理论分析和搭建实验样机验证，该拓扑具有以下特点：

（1）变换器实现了较高的电压增益，且不需要极大的占空比和匝比；

（2）变换器的开关管和二极管电压应力输出电压较低，故可以选择低电压等级器件；

（3）变换器具有传统Boost-Sepic 变换器输入电流连续的优点；

（4）变换器实现了开关管的零电压开通，又减轻了二极管的反向恢复问题。

基于上述优点，该变换器可用于需要高增益DC-DC 变换器的空间飞行器中。