三线扭摆法精确测量圆环转动惯量

安盼龙，赵瑞娟,，郑永秋

(1.陕西铁路工程职业技术学院，陕西 渭南 714000；2.中北大学测控技术与仪器国家级实验教学示范中心，山西 太原 030051)

转动惯量是描述刚体转动惯性大小的量度，是表征刚体特征的一个非常重要的物理量[1-3]。转动惯量与质量不同，其值不仅取决于转轴的位置，还与物体的质量分布情况有关。如果刚体形状简单，且质量分布均匀，可以利用连续积分直接计算出绕特定轴的转动惯量，另外理论计算时还可以结合平行轴定理及垂直轴定理。然而在工程实践中会不可避免碰到大量的形状复杂，且质量分布不均匀刚体，导致理论计算极其复杂，这种对的情况下往往采用实验方法来测定[4,5]。测量刚体转动惯量的方法有多种，三线摆法具有设备简单、直观、方便测试、精确度高的优点，另外扭摆在运动过程涉及数学近似处理、角谐振动等复杂问题，向来是研究的热点[6-8]。

1 实验原理

密度分布均匀质量为m环的均匀圆环，内外直径分别为D1为D2，对通过其圆心且垂直于圆环平面的转轴的转动惯量J计算公式为(J单位：kg·m2)

(1)

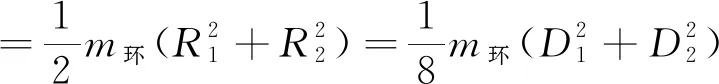
根据转盘动能与势能相互转化的能量守恒定理

(2)

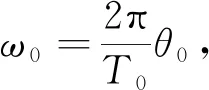
图1 待测钢质圆环

1.1 三线扭摆自身圆盘的转动惯量

(3)

作H≈L近似处理，L为摆线长，T0为扭摆自身的振动周期，t0=100T0。

1.2 圆环扭摆转轴共线总转动惯量

(4)

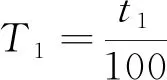
T1为扭摆加圆环共同振动的周期，t1=100T1。

1.3 均匀圆环的转动惯量

J=J1-J0

(5)

1.4 三线扭摆法测量的百分误差

(6)

2 实验测试

2.1 实验减小误差应注意的问题

2.1.1 调节三根摆线等长

要先使摆线等长，才能调节扭摆支架的竖杆，原因是一定要先使摆线等长，再使扭摆支架的竖杆与水平面垂直，因为调节竖杆的垂直，需要用到摆线做参考线；如果三根摆线不等长，从任何方向看，摆线都是倾斜的，起不到参考标准的作用。

2.1.2 多个周期同时测量

测量周期T时，不直接进行测量，而是测100T，原因为测量T时，如果计时器很准，误差主要来自起点和终点的确定误差；而如果一次测量100T，起点和终点的确定误差还是一样，但是用总的时间t除以100，最后得到T，在这个T中，起点和终点的确定误差影响就很小了。其他带有周期性的物理量，测量其周期，也可以这样做，以减小测量误差。比如测量螺杆的螺距，它有空间周期性，也可以先测出100倍的螺距，再除以100，算出1倍的螺距来。

2.1.3 平衡位置开始或停止计时

过平衡位置时，扭摆运动速度快，在此时开始或停止记录时间，误差不会太大；当趋于位移最大点时，扭摆振动速度慢，很难掐准在哪一个位置时，扭摆振动速度为0，这样，判断误差很大，对测量的影响就比较大。

2.1.4 确定扭摆扭动的角平衡位置

首先让扭摆摆动起来，然后将扭摆下方的水平杆扭转到振动的平衡位置，并将其上的指针转到合适位置，以方便角位移判断。

2.2 测试数据及处理

2.2.1 实验数据参数记录

实验数据参数记录见表1。

表1 实验直接读取测量参数

表2 空盘与空盘+圆环的测量数据

计算圆环转动惯量的理论值J理：

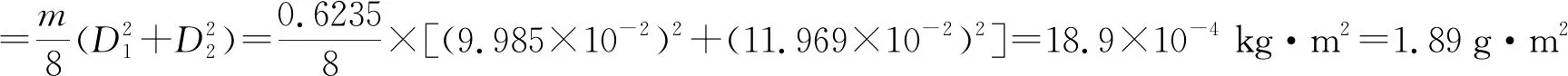
2.2.2 实验数据处理

实验数据处理见表3。

表3 实验数据处理

(1) 计算t、σt、T、σT

实验可知：

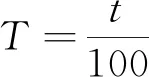
(2) 圆盘的转动惯量J0与σJ0

×(1.684)2=0.198×10-2kg·m2=1.98 g·m2

(3) 计算圆环与圆盘总的转动惯量J与σJ

=0.388×10-2kg·m2=3.88 g·m2

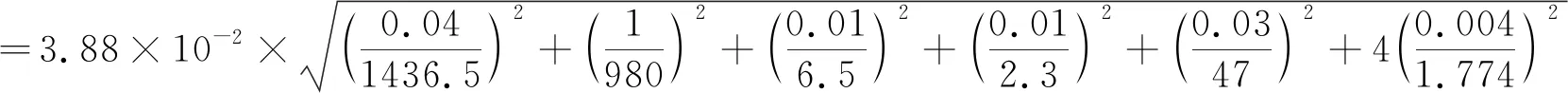
=0.02×10-3kg·m2=0.02 g·m2

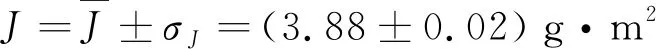
(4) 圆环的转动惯量J环与σJ环

=0.03 g·m2

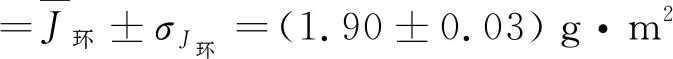
(5) 理论值与实验值百分误差E

3 结 语

通过对三线扭摆法测量钢质圆环转动惯量系统的研究，分析了测量误差产生的原因，详细计算了对称中心轴线空盘的转动惯量、空盘与圆环的转动惯量。最后根据误差的合成公式得到了圆环的转动惯量及其不确定度，经过实验，转动惯量的理论积分与实验值的相对百分比误差为0.5%，在实验允许的误差范围内。为进一步研究不确定度处理计算、三线扭摆的数学非线性特征及非规则几何物体的转动惯量的物理测量提供思路。