视角直接比较法测自组望远镜放大率方法的改进

钟 瑞,韩建卫,王 拴,纪 纬,张立彬

(哈尔滨工业大学(深圳) 实验与创新实践教育中心，广东 深圳 518055)

望远镜是一种非常基本、常用的目视光学仪器，了解其工作原理、掌握其组装方法及其放大率的测定方法对进一步掌握更复杂的光学仪器的使用都是非常必要的。当前的物理实验教材中，自组望远镜放大率的测定大多采用视角直接比较法[1]。这种方法简单直接，无须额外增加实验器材，但是存在以下问题：由于人眼的直接观察距离有限，通常在1～1.5 m范围以内，超过2 m之后，用两只眼睛同时观察目标尺实物及其经望远镜放大后的像较为困难，因此测量其放大率时，目标尺与物镜的距离(即物距)不能过大，通常限制在2 m以内；而另一方面，若物距太小，测得的望远镜放大率结果与其理论值相对误差会比较大。为克服以上矛盾，有文献提出了游码法[2]、分划板法[3]、比较板法[4]、成像公式法[4]等诸多改进方法。笔者在实验教学过程中发现，针对物距较小的情况，对望远镜放大率的计算公式进行适当地修正，即可在不额外增加实验器材、采用较短物距的前提下，精确地测得自组望远镜的放大率，使学生更加深刻理解望远镜成像原理。

1 开普勒望远镜放大率的理论值

开普勒望远镜的工作原理如图1所示，其物镜和目镜均为凸透镜，焦距分别为f1和f2(f1>f2)，物镜的后焦面和目镜的前焦面非常靠近，几乎重合。位于无穷远的物，先经物镜成一实像，像高为y′，位于物镜的后焦面上。该实像位于目镜的一倍焦距以内，且非常靠近目镜的前焦面，然后经目镜成一放大的虚像。人眼从望远镜的目镜中观察到的即为该放大的虚像，其像高为y″。放大后的虚像相较于被观察的实物，其对人眼的张角增大了，即人眼观察该物体的视角放大了。

图1 开普勒望远镜的工作原理

望远镜的视角放大率定义为：用望远镜观察物体时该物体的像对人眼的视角与人眼直接观察该物体时的视角的比值，由于视角很小，可以用其正切值代替。如图1所示，经过简单的几何推导，结合物镜的后焦面和目镜的前焦面几乎重合这一近似条件，可得到望远镜的无穷远视角放大率理论值Γ0为

(1)

即开普勒望远镜的无穷远视角放大率理论值为其物镜与目镜的焦距之比。

2 视角直接比较法测望远镜的放大率

具体操作如图2所示。将目标尺上的上、下指标间距设置为d1，然后将目标尺放置于距离望远镜物镜一定位置处，仔细调节物镜和目镜位置，直至能从目镜中看到清晰的上、下指标的放大像。

图2 视角直接比较法测望远镜的放大率实验装置

测量时，用一只眼睛从望远镜目镜中观察经望远镜放大后的上、下指标的像(间距为d2)，另一只眼睛直接观察目标尺实物。经过眼睛的适应性练习，并仔细调节物镜和目镜，消除视差，使得目标尺与指标像位于同一平面内且目标尺处于指标像的中间，如图3所示。然后利用目标尺直接测量指标像的间距d2，则该自组望远镜的放大率测量值Γ1为

(2)

该实验满足薄透镜对近轴光线的成像条件，物距u、像距v、薄透镜焦距f的关系满足高斯公式。

(3)

图3 放大像的尺寸测量

受实验室空间所限，实际的测量实验中，物距不可能无限远，加之人眼观察距离的限制，采用视角直接比较法测望远镜的放大率时，物距通常在2 m以内。在这种条件下，由式(3)可知，物镜对目标尺的上、下指标成的实像位于物镜的一倍和二倍焦距之间，且物距越小，像距越大，即该实像离物镜的后焦面越远。因此，物距越小，实际的放大率与式(1)计算得到的理论值差别越大，需要对计算公式(1)做修正。

3 开普勒望远镜放大率计算公式的修正

如图4所示，设被观察物的高度为y，其与望远镜物镜的间距为u1，经物镜成的实像高度为y′，该实像与物镜的间距为v1，与目镜的间距为u2，物镜与目镜的间距为L。

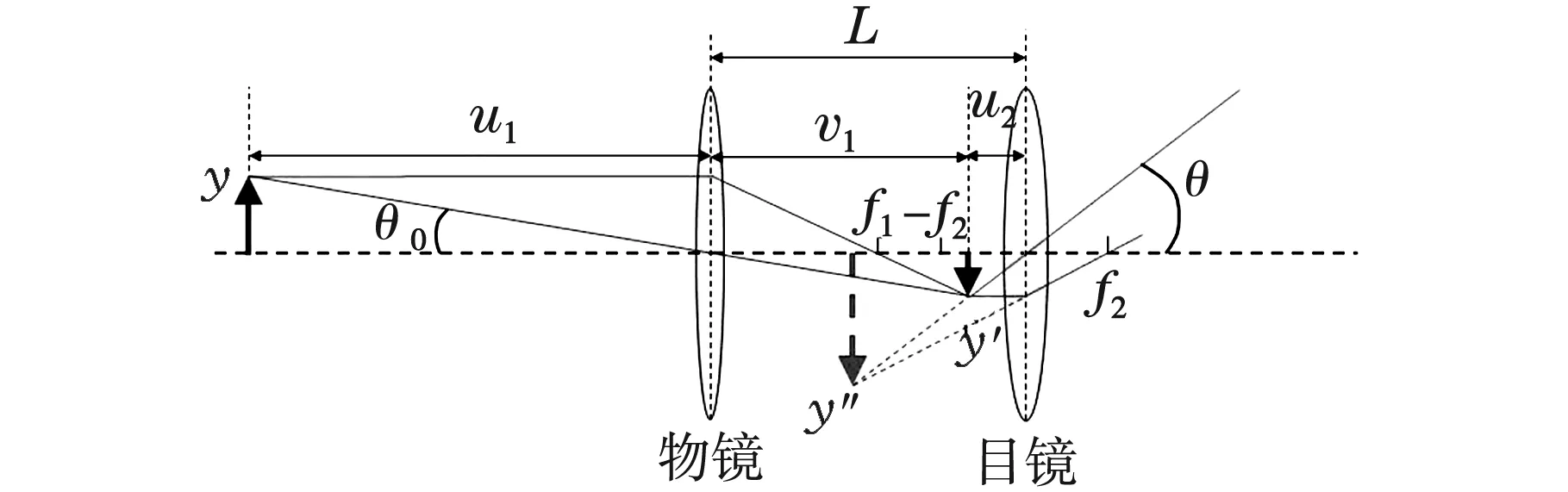
图4 开普勒望远镜观察有限远物体时的光路

望远镜的视角放大率计算值Γ2为

(4)

其中

(5)

(6)

根据高斯公式

(7)

由式(4)-(7)得到修正后的望远镜的视角放大率计算值Γ2为

(8)

可以看到，修正后的计算公式中不含目镜的焦距f2，看似与目镜的焦距无关。实际上，为了达到最佳的效果，该表达式中的物镜与目镜的间距L必须调节到一个合适的值。因此，修正后的放大率计算公式其实是与目镜的焦距相关的。

4 实验结果

实验装置如图2所示，物镜和目镜用相同型号的光学底座置于滑轨上，物镜焦距f1=225 mm，目镜焦距f2=45 mm，改变目标尺与物镜的间距(即物距u1)，测得不同物距对应的放大率数据如表1所示，由此得到自组望远镜放大率的测量值Γ1、修正后的计算值Γ2与物距u1的关系曲线如图5所示。

表1 视角直接比较法测望远镜的放大率数据

图5 自组望远镜的放大率与物距的关系曲线

为了使测量结果更精确，需要注意两个细节：仔细调节，消除视差，使得目标尺与指标像位于同一平面内且目标尺处于指标像的中间；当物距较远时，观察者用目标尺测量指标像的尺寸时，可能看不清目标尺上的刻度(因人而异，一般情况下，超过1.5 m就看不清)，可以两个人配合测量，观察者从目镜位置观察，配合者将一把直尺沿水平方向紧靠目标尺并沿竖直方向移动，当观察者观察到直尺的某条边分别与上、下指标像的边对齐时，让配合者读出目标尺上与直尺的这条边对齐的刻度，两次读数之差即为指标像的间距d2。

5 结 语

由表1及图5所示实验结果可以得到以下结论：

(1)随着物距的增大，视角直接比较法测得的望远镜放大率Γ1与无穷远视角放大率理论值Γ0的相对误差呈下降趋势；

(2)当物距小于2.5 m时，视角直接比较法测得的望远镜放大率Γ1与无穷远视角放大率理论值Γ0的相对误差较大，超过5%；

(3)视角直接比较法测得的望远镜放大率Γ1与修正后的计算值Γ2非常接近，即使在物距小于1.5 m时，二者的相对误差也非常小。

通过对开普勒望远镜的放大率计算公式进行修正，并结合实验验证，成功地对视角直接比较法进行了改进。该改进方法可以让实验者在物距较短的情况下精确测量自组望远镜的放大率，解决了学生在实验时遇到的实验空间受限、人眼观察距离受限的问题。