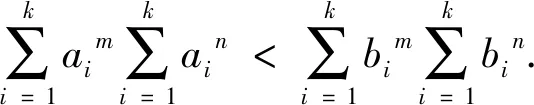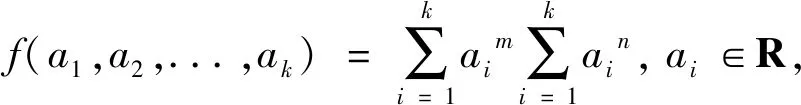一道奥赛不等式题的简证、变式与推广

湖南省桃江县第一中学 (413400) 胡芳举 湖南省岳阳县第一中学 (414100) 胡燕玲

题目已知实数a,b,c,d满足ad，证明：(a-b)(a2+b2)<(c-d)(c2+d2).

该不等式选自湖南师大沈文选教授主编的《奥赛经典.高一数学》(2004年出版).本文将给出该题的一个简证、三个变式及三个推广.

一、简证

设fs(x)=(x-s)(x2+s2),x∈R，则fs′(x)=3x2-2sx+s2=2x2+(x-s)2≥0，∴f(x)单调递增(与实数s的取值无关)，∵a

二、变式

变式1 已知实数a,b,c,d满足a

注：在原不等式中将b,d分别换成-b,-d可得上式，感觉这个不等式更和谐.

变式2 已知a-c>|b-d|，求证：a(a2+3b2)>c(c2+3d2).

证明：由题设知c-ac-d,a+b>c+d，∴(a-b)3>(c-d)3,(a+b)3>(c+d)3，由这两个不等式相加、化简即得要证不等式.

变式3 已知a-c>|b-d|，求证：a(a2+b2)>c(c2+d2).

证明：要证a(a2+b2)>c(c2+d2)，等价于证a3-c3>cd2-ab2，由变式2知a3-c3>3(cd2-ab2).若cd2-ab2≥0，则3(cd2-ab2)≥cd2-ab2，于是a3-c3>cd2-ab2；若cd2-ab2<0，因为a3-c3>0，故同样有a3-c3>cd2-ab2，所以变式3成立.

三、推广

1.从项数上推广可得

推广1 设ai

证明：设f(a1,a2,a3) = (a1+a2+a3)(a12+a22+a32),a1,a2,a3∈R，则fa1′ = 3a12+ 2(a2+a3)a1+ (a22+a32) =a12+ (a1+a2)2+ (a1+a3)2≥0，∴f(a1,a2,a3)关于a1单调递增，由于a1,a2,a3对称，∴f(a1,a2,a3)分别关于变量a1,a2,a3单调递增(就单调性而言各变量相互独立).∴由ai

2.从指数推广可得

推广2 设an>0，则(am+bm)(an+bn)<(cm+dm)(cn+dn).

(1)当t≥0时，显然g(t)>0，∴fa′>0；

(2)当t<0时，g′(t)=mntn-1(1+tm-n)，∴当t∈(-1,0)时,g′(t)>0,当t∈(-∞,-1)时,g′(t)<0，∴g(t)≥g(-1)=2n>0，∴fa′>0.

综上，总有fa′≥0，∴f(a,b)关于a单调递增.又由于a,b对称，故f(a,b)分别关于变量a,b单调递增，∴由a

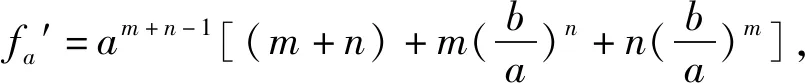
3.一般形式