多点开花 妙解三角形

福建省福清第一中学 (350300) 叶诚理 林品玲

在高三一轮复习后，学生对高中数学知识体系有了较为全面的认识，对数学思想方法有了一定程度的掌握，在解题过程中往往会从不同的角度考虑一个问题，产生了各种不同的解法，也许学生的过程与方法未必与标准答案一致，但其中不乏简洁、漂亮的解法，值得我们老师关注．以下是笔者在高三复习教学中遇到的一道解三角形的题目.

问题如图1，△ABC中，AC=2，AB=1，AD=k，点D为BC边上的动点，BD：DC=1:2，试求k的取值范围．

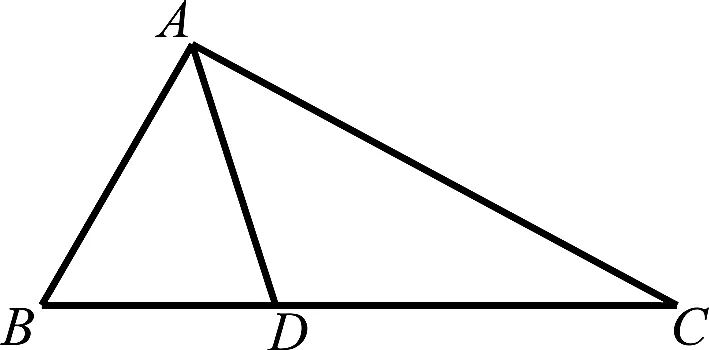
图1

本题考查学生运用余弦定理、诱导公式解三角形，求边的关系用到函数思想，化解三角函数关系式则考查了运算求解能力，试题难度较小，学生容易上手．

评注：该解法从点D分BC的比例入手，根据余弦定理，利用两角互补，算出AD的函数表达式，思路直接，易错点是忽略了三角形边的关系而求错定义域．

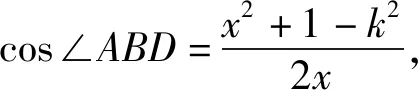
评注：该解法把同一个角B放在两个不同的三角形中，利用数学中对同一变量“算两次”的思想构建AD的函数表达式，与解法一可谓异曲同工．

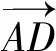
图2

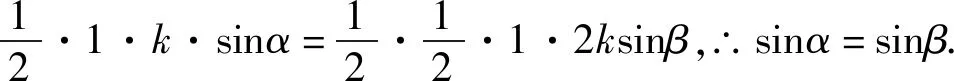
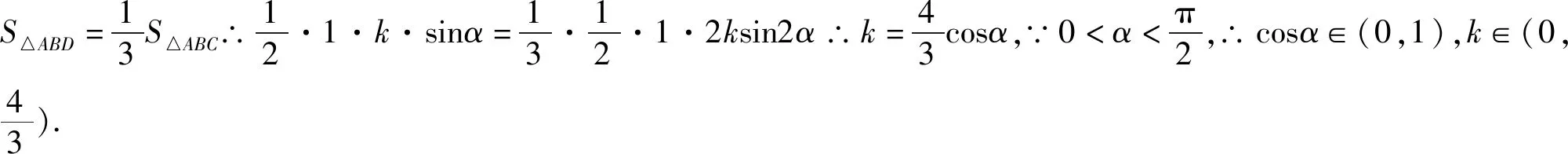
评注：该解法从等高的两三角形面积关系入手，证明AD为∠BAC的角平分线，揭示了问题的本质，打开解题思路，再次利用面积公式和三角恒等变换公式构建AD的三角表达式，十分巧妙．

评注：在证明直线AD为∠BAC的角平分线后，直接利用余弦定理解题，与解法一、解法二不谋而合．

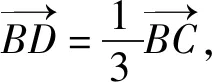
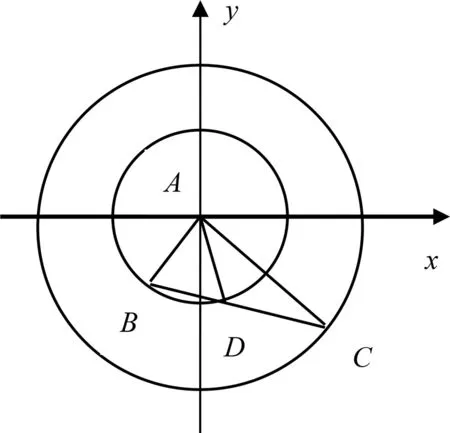
图3

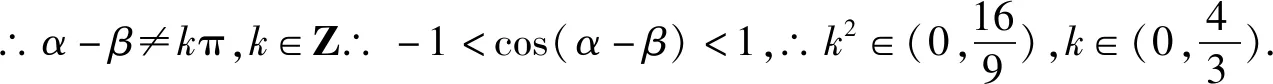
评注：该解法的亮点在于在原三角形图上建立平面直角坐标系，根据线段长度，巧设点的坐标，进而通过两点距离公式，再结合三角函数的性质得出线段AD的取值范围，体现了解析几何的特点：用代数的方法来研究几何问题．

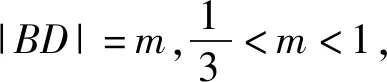
图4

评注：该解法也是通过建立直角坐标系来实现点的坐标表示，通过以点D为原点，突出了点A的几何特征：可看成以点B、C为圆心，1和2为半径的两个圆的交点，故可联立这两个圆的方程，算出交点轨迹，转化为求这个交点到原点的距离，其思路也十分巧妙．

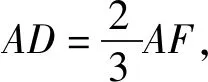
图5

评注：该解法充分利用已知三角形两邻边比为1:2，添加辅助线，构造等腰三角形，进而得出点D为新得的三角形的重心，再利用重心性质解题，该解法的精妙之处在于构造的辅助线使得问题的求解豁然开朗．

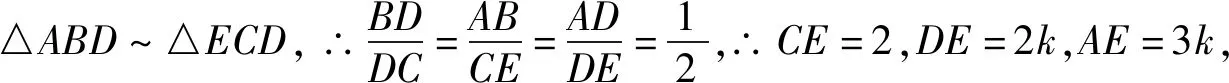
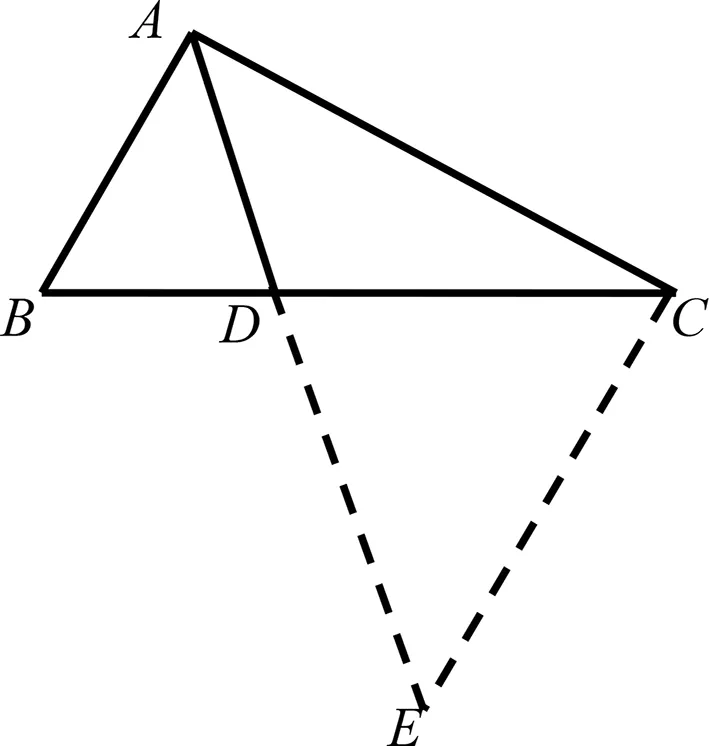
图6

评注：该解法通过构造相似三角形，利用相似比把所求问题集中到一个三角形中，直接利用三边关系建立不等关系，其思路返璞归真，计算量小．

解法十：(关注角变化，运用极限思想)角B的变化范围是大于0且小于π，由解法6的图3，固定AB边，当角B从0变大到π时，AD也跟着连续变大，下面用极限法考虑：

(1)当角B→0时，如图7，BC边上的高趋近0，此时AD→0;

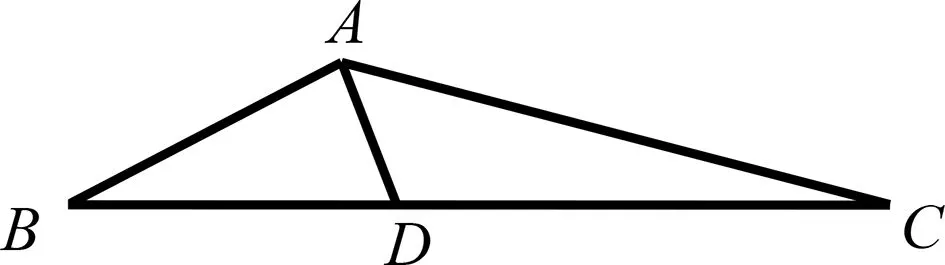
图7

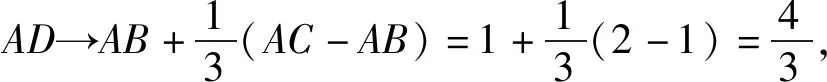
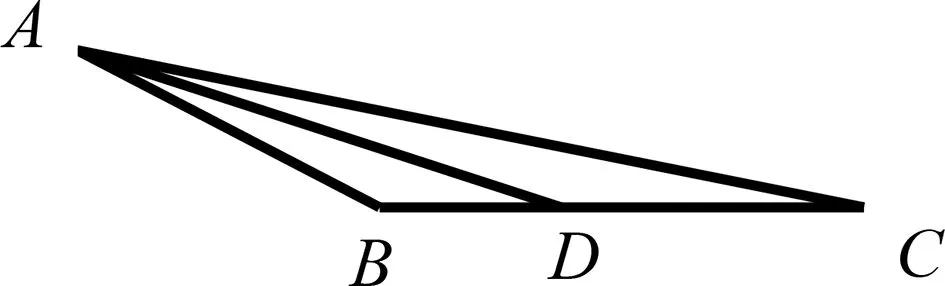
图8

评注：该解法从点B的变化趋势入手，单刀直入，从运动变化的观点，利用极限思想立竿见影地算出线段AD的取值范围，其思路简洁明了，令人拍案叫绝，美中不足在于其论证不够严密．

以上解法让学生感受到数学思维的无限魅力．解题中用到的知识涉及函数、方程、不等式、三角函数、平面向量、平面几何、解析几何等；集中考查了学生的抽象概括能力，运算求解能力和创新应用意识；用到的数学思想有函数与方程思想、化归与转化思想、数形结合思想、分类与整合思想，极限思想等．本题的一题多解，彰显学生灵活合理地运用所学知识解决实际问题的能力，是一道值得我们欣赏和品味的好题．