一道圆锥曲线问题的探究与拓展

江苏省常州高级中学 (213000) 黄龙孙 福建省厦门市海沧中学 (361022) 陈凌燕

圆锥曲线中有一类定点定值问题，是指在运动变化过程中，或动直线总是过某个定点，或交点总是在某条定直线上，或某个几何量(线段长，面积等)总是一个定值，蕴含了变化中的不变性，给人以一种奇妙的数学美的感受.同时这类问题通常具有入口宽、方法多但又需要扎实的学科技能和素养才能得以解决，本文以一道圆锥曲线问题的探究和拓展过程来展示这种数学的处理方法.

1 试题呈现

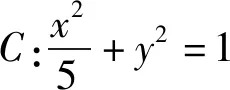
2 分析与解

思路1：设AB直线方程，用直线方程的参数表示M，N两点.因为AB在绕着右焦点F转动的过程中，M，N两点也随之改变，所以M，N两点的坐标与直线AB的位置有关，自然产生用直线AB方程的参数来表示的思路.

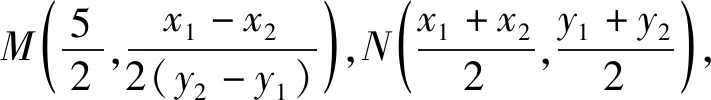
反思：从解法2过程来看，M,N的坐标直接用A,B的坐标来表示，省去了联立直线AB方程与椭圆方程的过程，不仅运算量更小，过程更简洁，同时也便于结论的推广.可见，只需满足AB是椭圆的动弦，中点为N，椭圆A,B处的切线相交于点M，则O，M，N三点共线.

3 探究拓展

解完题后我们用几何画板演示可以直观地看到在AB变动的过程中，O，M，N始终三点共线，而且M点也一直在椭圆的准线上运动，同时更为简洁的解法二也更具一般性，这让我们感受到数学的奇异美和满足感，以及继续探究的跃跃欲试之感.

问题1：能否将交点M在定直线上推广到一般椭圆上？

问题2：如果AB直线过的定点不是焦点，那么交点M会在定直线上吗？直线方程是什么？

问题3：逆向思考，反之，如果已知定直线上的动点M向椭圆引切线，则两切点所在的直线会过定点吗？

问题4：O，M，N三点共线能否推广到一般椭圆上？

结论3、结论4证明略.

问题5：双曲线和抛物线能否有类似的结论？

回答是肯定的，以下给出了课后学生探究得到的结论，此处篇幅所限，略去证明.

命题5 抛物线C:y2=2px(p>0)上一点A(x0,y0)处的切线方程为y0y=p(x0+x).

命题6 若AB是抛物线C:y2=2px(p>0)的动弦，且过定点(x0,y0) ，则抛物线C在A，B处的切线的交点M在定直线l:y0y=p(x0+x)上.

命题7 若M在定直线l:y0y=p(x0+x)上，过M作抛物线C:y2=2px(p>0)的切线，切点分别为A，B，则直线AB过定点(x0,y0).

命题8 已知AB是抛物线C:y2=2px(p>0)的动弦，中点为N，抛物线C在点A，B处的两切线的交点为M，则MN∥x轴.

4 教学启示

圆锥曲线问题具有很好的探究价值，一是不同的解法运算量和运算难度不同，找到一个简洁的解法会产生很强的满足感，二是蕴含着丰富的数学思想，例如特殊到一般，数形结合等，三是解完题后继续将成果推广到一般情形或者逆向思考，交换条件和结论研究逆命题等，能够激发学生的好奇心和求知欲，让学生的自主探究的过程中，掌握数学研究的方法，提高学科素养，领悟数学思想，并体会数学的奇异之美，真正享受学习数学的快乐！