思想来引航，命题有方向

福建省福清第三中学 (350315) 唐 洵

近日，笔者有幸受到某考试机构的邀请，参与其联考试卷的命题工作.期间，以函数导数为背景，命制了文科解答题的压轴题，试题以导数为工具，对函数的性质进行研究，并在不等式恒成立的背景下求解参数的取值范围，此题虽然作为全卷的压轴，但由于高三学生一轮复习尚未结束，知识体系尚未建构完整，因此考试机构给出的命题要求是，试题难度不可太大，解题应注重通性通法，但试题要具有一定的区分度，尽可能体现数学的核心素养以及近年全国卷的命题趋势与命题风格.

题目已知函数f(x)=(x-2)ex+2.(1)求函数f(x)的极值；(2)若关于x的不等式2f(x)+n(x2+4x)≥0在[0,+∞)上恒成立，其中n≥0，求实数n的取值范围.

本题拟考查利用导数工具研究函数的单调性、极值、最值以及不等式等问题，考查数学抽象、逻辑推理、数学运算、直观想象的核心素养，考查化归与转化思想以及分类与整合思想.

首先，先命制压轴部分与不等式相关的问题，考虑到难度因素，我们选择了最简单的一个不等关系，x2≥0，这对任意x∈R恒成立，于是将初始函数设定为f1(x)=x2.其具体命制过程如下：

步骤一：化归与转化思想定向.

由于近年来新课标I卷的导数试题都与ex、lnx之间建立了密不可分的联系，于是我们考虑在x2≥0的不等关系下，融入ex≥x+1，使得试题具有一定的难度.

步骤二：数形结合思想引航.

第(1)小题是后续试题的雏形，考虑到即使是文科，本题难度也略显简单，学生在求解时可以直接通过放缩直接得到答案，不足以作为压轴部分，我们考虑扩大不等式成立的区间.通过几何画板构造函数f3(x)的图像如图1所示，观察可知，函数f3(x)的图像始终不落在x轴的下方，于是得到第(2)小题：求证：f3(x)≥0在(-∞,+∞)上恒成立.

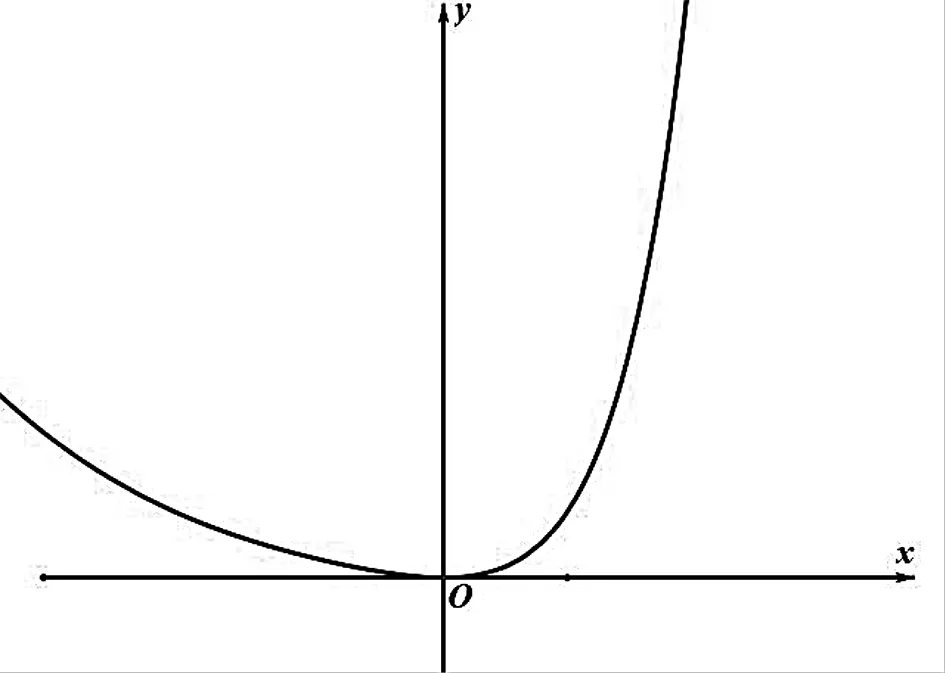
图1

步骤三：分类与整合思想延伸.

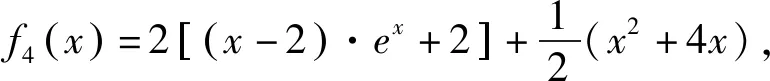
步骤四：函数与方程思想点睛.

为了照顾数学学习中的“弱势群体”，提升学生数学学习的兴趣及信心，问题(1)的设定尤为关键，命题的主干思想是通过检测学生导数工具的基本使用能力，进而达到对函数与方程思想的考查，于是我们将函数f5(x)中没有参数的部分抽出，得到函数f(x)=(x-2)ex+2，进而研究函数f(x)的极值，于是便得到了文章开头所呈现的试题.

下面给出试题的解析过程：第(1)小题的解答比较简单，其解题步骤如下：

依题意，f′(x)=(x-1)ex，令f′(x)=0解得x=1；当x∈(-∞,1)时，f′(x)<0，当x∈(1,+∞)时，f′(x)>0，故函数f(x)在(-∞,1)上单调递减，在(1,+∞)上单调递增；从而当x=1时，函数f(x)有极小值f(1)=2-e，无极大值.

第(2)小题：涉及含参不等式的解法，解题时入口较多，我们提供如下解法以供大家参考.

方法一：(整体构造)设h(x)=2f(x)+n(x2+4x)=(2x-4)ex+n(x2+4x)+4，故h(x)≥0.因为h′(x)=(2x-2)ex+2n(x+2)=m(x)，令m′(x)=2xex+2n， 因为n≥0，有m′(x)≥0，此时m(x)在[0,+∞)上单调递增，则m(x)≥m(0)=4n-2.

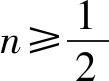
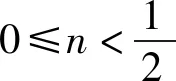
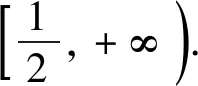
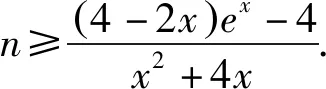
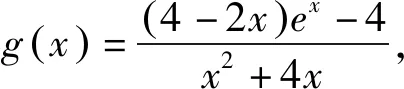
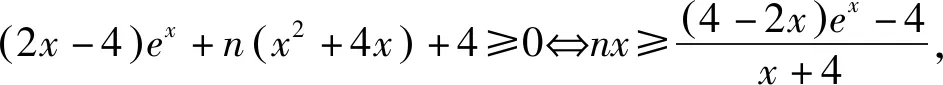
图2

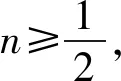
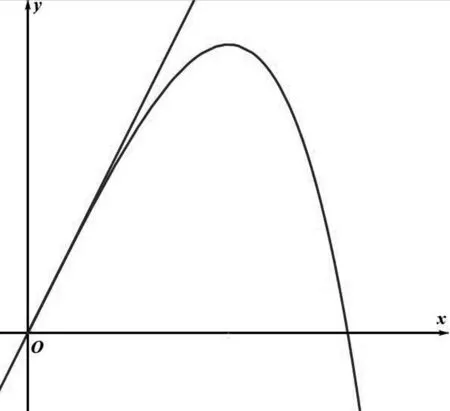
图3

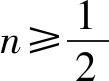
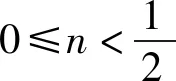
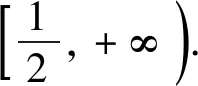
基于上述命题手法，我们再编制两道试题与大家共赏：

题1 若关于x的不等式(x+2)lnx-ax2+(1-a)x-1≥0在[1,+∞)上恒成立，求实数a的取值范围.

题2 若关于x的不等式(x+1)sinx-axex≥0在[0,+∞)上恒成立，求实数a的取值范围.